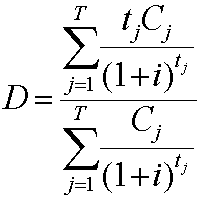
Latest Revision: October 30, 1995.In 1938, Frederick Macaulay suggested a method for determining price volatility of bonds. He gave the name duration to the measure, but it is now often called Macaulay duration. The formula that he gave is:
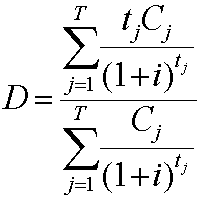
where:
Since there was very little volatility of interest rates, due to regulation, few people paid attention to duration until the 1970s when interest rates started to rise dramatically. Investors and traders became very enamored with any tool which would tell them how much the prices of bonds would change for a given change in yields.
Macaulay duration can be used to determine the following:
While all of this is useful, it did not tell investors exactly how much a bond's price changes given a change in yield. However, it was noticed that there is a relationship between Macaulay duration and the first derivative of the price/yield function. This relationship lead to the definition of modified duration:

where:
This formula can be used to estimate the change in price for a small change in the periodic yield:

Modified duration became recognized as a better measurement of interest rate risk than Macaulay duration. But it still was not perfect. Most Treasury bonds and corporate bonds pay twice per year. If the semiannual yield was 10%, then the periodic yield is 5%, so the Macaulay duration should be divided by 1.05 to get the modified duration. But not all bonds pay semiannually. For example, Eurobonds pay yearly, and mortgage-backed securities pay monthly. The modified duration of a Eurobond showed its interest rate sensitivity to a change in the annualized rate, but a Treasury bond's modified duration showed its sensitivity to a change in the semiannual rate. This made it difficult to compare the price volatilities of bonds with different payment periods. One way around this problem was to do all of the calculations with semiannual yields.
By the mid 1980s, another problem arose. A lot of corporate bonds were issued with call features. These features allowed the companies that issued these bonds to call them back at a set price if it was to their advantage. With interest rates rising in the late 1970s and early 1980s, very few people paid attention to these call features. It made little sense for a company to refinance a bond with a 9% coupon rate if the current rate had risen to 14%. But by the mid 1980s interest rates started to drop, and companies began refinancing their bonds at lower rates. Investors who thought that they had a long term investment at a high interest rate suddenly found themselves having to reinvest their money at lower rates.
Several investment banks started pricing these bonds differently. Instead of using a yield to maturity, they would calculate the price of the bond assuming that it would be called at the worst possible time. The call date which gave the lowest yield was called the worst call date. They calculated a duration, assuming this worst call date. This was a better estimate of interest rate sensitivity for these bonds.
While better, it still turned out to be unsatisfactory. If a callable bond were trading near par, then a small drop in the yield might mean that it would be called in six months -- so it would only have a small increase in value. On the other hand, a small increase in interest rates might indicate that it will trade until maturity -- so it could have a large drop in value. Some investment banks started looking at "one-sided" durations, or did what-if analyses, looking at what happens to the bonds under a few interest rate scenarios.
In the mid 1980s, Salomon Brothers developed an options pricing model for callable bonds. Other firms quickly followed their lead. At the heart of the options pricing model is an interest rate process. Instead of looking at a few interest rate scenarios, they looked at thousands of possible interest rate paths through time. These paths are derived from the Treasury curve. For each of these interest rate scenarios, they could predict the probable set of cash flows, and could calculate a present value for those flows. By assigning a probability to each of these paths, an expected present value of the bond can be calculated.
The interest rate paths represent short term Treasury rates through time. If we discount all of the cash flows by these Treasury rates, and then average the present values using the probability weights, we will get a present value for the bond. This is the price that someone should pay for this bond if it had the same credit risk as Treasury bonds. But corporate bonds are riskier than Treasury bonds, so investors expect a higher return. If we knew how much higher the return should be, we could just add that value to each of the interest rates in each path. The value that we add on to the rates is called the option-adjusted spread (OAS). By discounting all of the cash flows by these new rates, we can find the present value of the bond. If the price of the bond is already known, then the process can be reversed to solve for the OAS.
With these tools, the options pricing model (often called an OAS model) can be used to calculate the true interest rate sensitivity of the bonds. If an investor had a way of estimating the price of the bond for a small change in interest rates, then he could estimate the derivative of the price/yield function by setting up a difference equation. If this value is then divided by (-Price), the true duration can be estimated. For bonds with imbedded options, this value will frequently differ from the modified duration. This new type of duration is sometimes called option-adjusted duration, but is also known as effective duration. Note that the shift of the yield curve is a parallel shift of the semiannual yield. If the bond had fixed cash flows, then the effective duration of a bond with fixed cash flows is just the Macaulay duration divided by (1+i/2). For bonds which pay semiannually, this is just the modified duration.
The formula for effective duration is:

Where:
If P is known, then Pup and Pdown can be calculated by doing the following: