
Copyright 1995 by Campbell R. Harvey. All rights reserved. No part of this lecture may be reproduced without the permission of the author.
Latest Revision: December 4, 1995.
So far in the course, we have not established any benchmarks to compare securities or portfolios other than expected returns. It is impossible to judge the quality of an investment be simply looking at its expected returns. For example, consider an advertisement from Wall Street Journal.
| The Franklin Income Fund | 516% | Dow Jones Industrial Average | 384% | Salomon's High Grade Bond Index | 273% | Cost of Living | 169% |
These are average returns over the past 15 years than the Dow Jones Industrial Average and Salomon's High Grade Bonds. Does this mean that we can beat the market by investing in Franklin now? The answer is no. The advertisement tells us nothing about the risk of the Franklin Fund. We will always want to consider risk as well as return. The Franklin Fund stocks may be very risky and the only way people will hold the component stocks is to have a high expected return. So we have go beyond returns and develop a model of risk that allows us to compare stocks and portfolios. [By the way, this ad last appeared in September 1987.]
There are many models of risk and return. Two popular models are: the Capital Asset Pricing Model (CAPM) and the Arbitrage Pricing Theory (APT). We will spend most of our time examining the Capital Asset Pricing Model. The CAPM was the first of the pricing models [William Sharpe (1964)] and the most commonly used by practitioners. The APT is examined in considerable detail in the elective courses. I will briefly introduce these models after we have finished with the CAPM.
The Capital Asset Pricing Model is an equilibrium model. The prices that exist in the economy are a result of all consumers maximizing utility and markets clearing, i.e. prices are set such that supply equals demand. Our goal is to create (model) a simple economy with these ingredients and see if the pricing function has power to predict actual prices in the economy. A simple economy involves simple assumptions. After we derive the CAPM, you will note that many assumptions have been made that are not very realistic. But caution should be taken in judging a model by its assumptions. It is often better to judge a model by its ability to predict.
The consumers in our model are rational utility maximizers. The objective of each person is to maximize utility of consumption today, plus the expected utility of wealth, EU(W), (future consumption) tomorrow. Mathematically, the consumer choses c0 consumption today. Importantly, wi are the portfolio weights for the n assets we could invest in today.
We will also assume that
U'>0 and U''<0
These are conditions on the form of the utility function.
The first derivative being greater than zero means that you prefer
more wealth to less wealth. This is a property that is not controversial.
The second derivative being negative means that you prefer more to
less at a decreasing rate as wealth gets larger. So you get more
utility from a $10,000 increase in you wealth if your previous
wealth was $20,000 rather than $2,000,000.
The variables under the maximand are the control variables. The consumer will be choosing: consumption today, c0, and investment proportions in N assets, wi. We will assume that one of these assets, i=0, is riskfree. So the consumer will use his initial wealth for either consumption today or investment in assets that pay off in the future. A constraint is necessary:
In one of the early lectures, I said that a person is risk averse if she prefers $50 for sure rather than a 50-50 gamble with payoffs of $0 and $100. Let's be more precise about what we mean here.
The first thing that we have to establish is what prefers means. In economics, we associate preference with higher utility. In an uncertain environment, a person (whatever their attitude toward risk) prefers higher expected utility. It will be the shape of the utility function that will determine the attitude towards risk.
Now lets consider three types of utility functions. It will be assumed that a person gets utility only from wealth. This will enable us to construct some simple examples and it greatly simplifies the pricing problem. On the y-axis the utility is plotted. On the x-axis, the wealth is plotted. We will consider the example of the gamble in the first paragraph.

In this case, utility from the expected wealth, i.e., U(.5 x $100 + .5 x $0), exceeds the expected utility, i.e. .5 x U($100) + .5 x U($0). This is exactly the example in the first paragraph. The person would rather take the expected value of the gamble ($50) rather than the gamble itself.

In the case of risk neutrality, the person is indifferent about taking the gamble or taking the expected payoff. I mentioned this possibility when discussing the intuition behind the Black-Scholes option pricing model. The utility function is linear. This means that the utility of the expected payoff is equal to the expected utility of the payoff.

In this case the person prefers the gamble to the sure thing. Because of the shape of the utility function, the utility of the expected payoff is less than the expected utility. The person would not accept the $50 if faced with a choice between the $50 and the gamble with payoffs $0 and $100.
In financial economics, we assume that people are risk averse. If the person is faced with the choice of two portfolios and the expected return on both is 50% but on one portfolio the payoffs are 50-50 on a 0% and 100% payoff while the other portfolio paid 50% for sure, then the person will choose the portfolio that pays 50% for sure.
In terms of the distribution of the payoffs, the gamble which on average has a 50% payoff has a higher variance than the choice that pays off 50% for sure (zero variance). So we can say, if the payoffs are normally distributed, for a given mean payoff, we prefer the gamble with the lowest possible variance.
Suppose we are in a simple world with only two securities: those mentioned above. If everybody is risk averse, then no one will hold the security that has payoffs of 0% or 100% with equal probabilities. In order to get people to hold the security, you will have to raise its expected return to a point whereby the expected utility of holding the security is equal to the expected utility of the sure thing security. The key to finance is to find a relation whereby we can determine the exact amount of extra expected return needed to get somebody to hold the security.
At this point, we can only make general statements. The size of the extra expected return we have to give will be determined by two factors: the shape of the utility function and the variance of the gamble.
We can say something about the shape of the utility function in terms of its slope and its concavity. The slope is measured by the first derivative. The concavity is measured by the second derivative. In all risk classes, the slope of the utility function is positive (U'(W)>0). This simply means that I prefer more wealth than less. This holds whether I am risk averse or a risk lover. The concavity of the utility function determines the degree of risk aversion. Concavity means that magnitude of the slope is decreasing as we move to higher wealth levels. The second derivative is negative. In the case of risk neutrality, this second derivative is zero. In the case of risk loving, this second derivative is positive (convexity). We can think of the degree of risk aversion being determined by how concave the utility function is (how negative the second derivative is or more precisely how negative the ratio of the second and first derivatives is).
The size of the extra expected return will also be linked to the variance of the gamble. Indeed, the trivial case is a zero variance. The extra expected return in this case is zero. As the gamble has a higher variance the extra expected return must increase for a given level of risk aversion.
We can delve deeper into this problem by trying to measure the cost of risk. Above we were trying to get some intuition as to the factors that would affect the risk-return trade off. We suggested the concavity of the utility function and the variance of the gamble. It is clear that the individual will never take a fair bet (i.e. 50% probability of a $1 payoff and a 50% probability of a -$1 payoff). He is better off with his initial wealth.
Now let's look at the problem from a different angle. The question is: how much would an individual pay to avoid a fair bet of size plus or minus h? Think of this as an insurance problem. The amount that you are willing to pay, p, is the insurance premium. Indifference implies:
U(W-p)=.5 x U(W+h)+ .5 x U(W-h)
To solve the problem, we need to isolate p on
the left-hand side of the equation.
This is complicated by the fact that p is inside the function.
The method to do this is to take a Taylor series approximation
to both sides of the equation. This is a good time to review
Taylor series.
The general formula for a Taylor Series expansion is:
Now back to our problem. Our strategy will be to take Taylor series approximations of both sides of the equation. If the size of p is small compared to the wealth W then we can ignore the second order and higher terms in the Taylor series. Note we are just plugging into the Taylor series formula above. To follow note that f()=U(), x=W, and j=-p. So the left hand side is:
U(W-p) approx= U(W) - U'(W) x p
The right-hand side is trickier. First, we cannot as easily ignore the
higher order terms. This is because h may take on values that
are considerably different than W.
So on the right-hand side we will take
a second order Taylor series expansion:
.5U(W+h) + .5U(W-h) approx=
.5{U(W) + U'(W)h + .5U''(W)h^2}
+ .5{U(W) + U'(W)h + .5U''(W)h^2}
approx= U(W) + .5h^2U''(W)
Note in terms of our formula for Taylor series: x=W and h=j,-j. Now equating the two expansions:
U(W) - U'(W) x p = U(W) + .5h^2U''(W)
We can solve for the insurance premium, p:
p=.5h^2[-U''(W)/U'(W)]
In words, the insurance premium can be expressed:
Insurance premium = .5x[Variance] x [Risk Aversion]
We can also think of this insurance premium as the cost of risk.
The cost of risk is proportional to the variance in wealth. Note that
all the terms that we expected to be in the expression are there. The ratio
of the derivative controls the concavity. The variance of the gamble
is also there. Note also that the cost of risk is positive because the
second derivative is negative. Also note that this is only an approximation.
This is sometimes referred to as coefficient of absolute risk aversion.
We need to know the following.
The portfolio return is just the asset returns times the weights each of the assets has in the portfolio.
That is, if we have $1 million to invest and we place $100,000 in security i, then w_i=.10
The weights sum to one.
This means that all money must be allocated.
The portfolio expected return is just the expected asset returns times the weights each of the assets has in the portfolio.
where E represents the expected returns on the various assets.
The portfolio expected excess return is just the expected returns on the assets minus the risk free return (say a one month Treasury bill) times the weights each of the assets has in the portfolio.
where EX represents the expected excess returns on the various assets.
The variance of the portfolio return is just
where V is the variance-covariance matrix (variances along diagonal and covariances in off diagonal).
The covariance of two portfolio returns, each denoted by their own set of weights, say w_a, w_b is just
where V is the variance-covariance matrix (variances along diagonal and covariances in off diagonal).
Remember the formula for correlation. The correlation of portfolio return a and b is just the covariance divided by the product of the standard deviations.
Given an optimal choice for today's consumption, c_0, the goal of a portfolio is to maximize the utility (expected) of future consumption provided by wealth at t=1. This is a hard problem.
Often we need to make a major assumption to simplify the problem. We will assume that asset returns are jointly normally distributed. The normal distribution has the property that the distribution can be completely described by two parameters: the mean and variance. The multivariate normal can be completely described by the means, variances and the covariances between the different assets.
Note the variances and the covariances of the riskfree asset are zero.
A linear combination of normals is normal. Therefore, wealth at t=1 is normally distributed. The entire probability distribution of wealth is described by portfolio's mean and variance. This all implies that a sufficient set of statistics to discriminate between portfolios is the mean and variance. This greatly simplifies the portfolio selection problem.
While most of finance is set in a mean-variance framework (which lends itself to using the normal distribution), there is some new work going on which tries to capture more general distributions. Harvey and Siddique (1995) have cast the portfolio selection in terms of mean-variance-skewness. This idea originates with important work in the 1970s. Harvey and Siddque make the means, variances and skewness dynamic processes which change with economic conditions. This paper is discussed in Tactical Global Asset Allocation.
Now let's consider the effect of diversification. We will examine a portfolio of two assets. From our formula for variance, we know:
Var_p = V_p = w'Vw
For the two asset case:
V_p =w_1^2 x V_1 + w_2^2 V_2 + 2 x w_1 x w_2 x V_12
We could also write this in terms of correlation:
V_p =(w_1^2 x V_1) + (w_2^2 V_2) + (2 x w_1 x w_2 x STD_1 x STD_2 x Corr_12)
where STD denotes the standard deviation.
For simplicity, assume that the variances of the two assets are equal, or V_1=V_2=V and that the portfolio weights are identical, or w_1=w_2=.50.
The first case of interest is that of perfect positive correlation. Using the formula:
V_p=.25 x V + .25 x V + (2 x .5 x .5 x V) = V
This result demonstrates that the portfolio variance is the same as the variance for each asset. So diversification does not reduce the portfolio variance in this case.
The second case of interest is that of zero correlation. Again, plugging into the formula:
V_p=.25 x V + .25 x V + (2 x .5 x .5 x V x 0) = .5 x VThis result demonstrates that the portfolio variance is half of the variance of the individual assets. So combining stocks that have less than perfect positive correlation is a strategy that will reduce the variance of the returns on your portfolio. This is called diversification.
The following graphs tells the story. Suppose we randomly selected a stock and plotted its standard deviation. Now we randomly draw another stock and plot the standard deviation of the equally weighted portfolio. We continue the exercise. Just be randomly selecting stocks we can decrease portfolio variance.
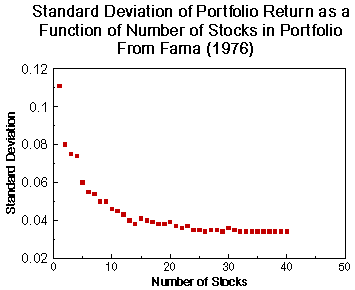
Consider forming a portfolio with three assets. The expected return vector is
(.090 .030 .007)
V = (.030 .100 -.020)
(.007 -.020 .010)
The standard deviation is calculated by taking the square root of the diagonal elements in the V matrix.
sqrt{.09}=.300
sqrt{.10}=.316
sqrt{.01}=.100
The correlation coefficient can be calculated with:
Corr_ij=V_ij/(STD_i x STD_j)The covariances can be found in the V matrix.
V_12= .030 V_13= .007 V_23=-.020
Solving for the correlation coefficients:
Corr_12 = .030/(.300 x .316) = .316 Corr_13 = .007/(.300 x .100) = .230 Corr_23 = -.020/(.316 x .100) = -.630
The variances of the portfolios are:
Var(Portfolio_1) = .028660 Var(Portfolio_2) = .034620
The covariance between portfolio 1 and 2 is:
Cov(Portfolio_1, Portfolio_2) = .029040
Previously, we made the simplifying assumption that asset returns are multivariate normally distributed. This assumption implies that individual asset returns are univariate normally distributed. We make the assumption of normality because it greatly simplifies the portfolio selection problem. The entire distribution of an individual stock's return can be described by two parameters: the mean and the variance. We can figure out a portfolio's mean and variance by examining the means, variances and covariances of the component securities. Most importantly, we can compare different portfolios on the basis of mean and variance.
Our discussion of utility functions and risk aversion provided two conclusions. First, consumers like more to less. In terms of a security or portfolio, consumers prefer more return to less return. Second, consumers like less variance to more variance. Remember that the risk averse consumer will always turn down a fair bet. In terms of a security or portfolio, the consumer will prefer a portfolio with less variance to another higher variance portfolio with an equal expected return.
These insights lead to two rules of portfolio selection.
A portfolio that satisfies these conditions is known as an efficient portfolio. A portfolio is inefficient if there exists another portfolio with:
We will now consider an example of the effects of diversification. Previously, we combined securities and looked at the effect on the portfolio variance for different correlation coefficients between the securities. We found that using equal weights in the two portfolios, a lower the correlation coefficient led to lower portfolio variance. In this example, we will look at a given correlation and vary the portfolio weights to trace the effect on the portfolio variance.
The example comes from a classic article by Bodie and Rosansky, "Risk and Return in Commodity Futures" which was published in the Financial Analysts Journal in 1980. We will trace out the return and standard deviation of a portfolio of common stocks and futures. A number of tables are presented.
Tables 2 and 3 document the cumulative wealth relatives and the year by year rates of returns of five portfolios from 1949 to 1976.
TABLE II Index of Year-End Cumulative Wealth Relatives, 1949-76
Number Long-Term U.S.
Common Commodity Of Government Treasury Consumer
Year Stocks Futures Commodities Bonds Bills Price Index
1949 1.000 1.000 - 1.000 1.000 1.000 1950 1.317 1.526 10 1.000 1.012 1.058 1951 1.633 1.934 10 0.51 1.027 1.121 1952 1.933 1.910 10 0.972 1.044 1.131 1953 1.914 1.789 10 1.007 1.063 1.137 1954 2.922 2.056 13 1.080 1.073 1.132 1955 3.844 1.957 13 1.066 1.089 1.136 1956 4.096 2.246 13 1.006 1.116 1.168 1957 3.654 2.193 13 1.081 1.151 1.204 1958 5.239 2.164 15 1.016 1.169 1.225 1959 5.863 2.176 13 0.993 1.203 1.244
Number Long-Term U.S.
Common Commodity Of Government Treasury Consumer
Year Stocks Futures Commodities Bonds Bills Price Index
1960 5.892 2.174 13 1.129 1.235 1.262 1961 7.477 Z.208 13 1.140 1.262 1.270 1962 6.824 2.227 13 1.219 1.296 1.286 1963 8.380 2.735 13 1.213 1.337 1.307 1964 9.762 3.067 14 1.277 1.383 1.322 1965 10.977 3.393 16 1.286 1.438 1.348 1966 9.872 3.890 17 1.333 1.506 1.393 1967 12.239 4.050 19 1.210 1.570 1.436 1968 13.593 4.101 19 1.207 1.651 1.503 1969 12.437 4.955 21 1.146 1.760 1.595
Number Long-Term U.S.
Common Commodity Of Government Treasury Consumer
Year Stocks Futures Commodities Bonds Bills Price Index
1970 12.935 5.550 22 1.285 1.877 1.693 1971 14.787 5.734 23 1.454 1.957 1.739 1972 17.592 7.666 23 1.537 2.032 1.799 1973 15.013 15.450 23 1.520 2.174 1.957 1974 11.037 20.389 23 1.586 2.347 2.196 1975 15.144 19.571 23 1.732 2.483 2.350 1976 18.754 22.065 23 2.022 2.609 2.463
TABLE III Year-by-Year Rates of Return, 1950-76
Long-Term U.S. Rate
Common Commodity Government Treasury Of
Year Stocks Futures Bonds Bills Inflation
1950 31.71 52.61 0.06 1.20 5.79 1951 24.02 26.71 -3.94 1.49 5.87 1952 18.37 -1.16 1.66 1.66 0.88 1953 -0.99 -6.32 3.63 1.82 0.62 1954 52.62 14.88 7.19 0.86 -0.50 1955 31.36 -4.79 -1.30 1.57 0.37 1956 6.56 14.75 -5.59 2.46 2.86 1957 -10.78 -2.34 7.45 3.14 3.02 1958 43.36 -1.33 -6.10 1.54 1.76 1959 11.95 0.54 -2.26 2.95 1.50
Long-Term U.S. Rate
Common Commodity Government Treasury Of
Year Stocks Futures Bonds Bills Inflation
1960 0.47 -0.09 13.78 2.66 1.48 1961 26.89 1.55 0.97 2.13 0.67 1962 -8.73 0.87 6.89 2.73 1.22 1963 22.80 22.84 1.21 3.12 1.65 1964 16.48 12.13 3.51 3.54 1.19 1965 12.45 10.62 0.71 3.93 1.92 1966 -10.06 14.65 3.65 4.76 3.35 1967 23.98 4.13 -9.19 4.21 3.04 1968 11.06 1.24 -0.26 5.21 4.72 1969 -8.50 20.84 -5.08 6.58 6.11
Long-Term U.S. Rate
Common Commodity Government Treasury Of
Year Stocks Futures Bonds Bills Inflation
1970 4.01 11.99 12.10 6.53 5.49 1971 14.31 3.31 13.23 4.39 3.36 1972 18.98 33.71 5.68 3.84 3.41 1973 -14.66 101.54 -1.11 6.93 8.80 1974 -26.48 31.96 4.35 8.00 12.20 1975 37.20 -4.01 9.19 5.80 7.01 1976 23.84 12.75 16.75 5.08 4.81
TABLE IV Annual Rates of Return on Alternative Investments, 1930-76
Highest Lowest
#Yrs Mean Annual Annual
Std Std Ret Annual Return Return
Series Mean Dev Err Neg Loss^a (Year) (Year)
A. Nominal Returns
(per cent per year)
Common Stocks 13.05 18.95 3.65 7 11.46 52.62 -26.48
(1954) (1974)
Commodity Futures 13.83 22.43 4.32 7 2.87 101.54 -6.32
with Treasury Bills (1973) (1953)
Long-Term Govern- 2.94 6.53 1.26 9 3.86 16.75 -9.19
ment Bonds (1976) (1967)
U.S. Treasury Bills 3.63 1.95 0.38 0 8.00 0.86
(1974) (1954)
Rate of Inflation 3.43 2.90 0.56 1 12.20 -0.50
(1974) (1954)
Highest Lowest
#Yrs Mean Annual Annual
Std Std Ret Annual Return Return
Series Mean Dev Err Neg Loss^a (Year) (Year)
B. Real Returns^b
(per cent per year)
Common Stocks 9.58 19.65 3.78 9 13.11 53.37 -34.79
(1954) (1974)
Commodity Futures 9.81 19.44 3.74 11 3.64 85.24 -10.30
with Treasury Bills (1973) (1975)
Long-Term Govern- -0.31 6.81 1.31 13 6.55 12.11 -11.90
ment Bonds (1960) (1967)
U.S. Treasury 0.22 1.80 0.35 7 2.41 2.32 -4.39
Bills (1964) (1950)
Highest Lowest
#Yrs Mean Annual Annual
Std Std Ret Annual Return Return
Series Mean Dev Err Neg Loss^a (Year) (Year)
C. Excess Returns^c
(per cent per year)
Common Stocks 9.42 20.12 3.87 9 3.21 51.76 -34.48
(1954) (1974)
Commodity Futures 9.77 21.39 4.12 13 3.91 91.59 -10.05
(1973) (1975)
Long-Term Govern. -0.79 6.43 1.24 17 4.73 11.67 -13.40
ment Bonds (1976) (1967)
^a The mean annual loss is defined as the sum of the annual losses (negative rates of return) divided by the number of years in which losses occurred. ^b The real rate of return, Rr is defined by: (1+R_n)/(1+i) -1 where Rn is the nominal rate of return and i is the rate of inflation as measured by the proportional change in the Consumer Price Index. ^c The excess return is the difference between the nominal rate of return and the Treasury bill rate.
Table 5 gives the correlation matrix for the different returns.
TABLE V Correlation Matrix of Annual Rates of Return, 1950-76
Long-Term
Govern-
Commodity ment Treasury
Futures Bonds Bills Inflation
A. Nominal Returns
Common Stocks -0.24 -0.10 -0.57 -0.43
Commodity
Futures -0.16 0.34 0.58
Long-Term Gov-
ernment Bonds 0.210 0.03
Treasury Bills 0.76
Long-Term
Govern-
Commodity ment Treasury
Futures Bonds Bills Inflation
B. Real Returns
Common Stocks -0.25 0.14 0.18 -0.54
Commodity
Futures -0.36 -0.48 0.48
Long-Term Gov-
ernment Bonds 0.46 -0.38
Treasury Bills -0.75
Long-Term
Govern-
Commodity ment Treasury
Futures Bonds Bills Inflation
C. Excess Returns
Common Stocks -0.20 0.08 -- -0.48
Commodity
Futures -0.26 -- -0.52
Long-Term Gov-
ernment Bonds -- -0.20
We will be concerned with the common stocks and the commodity futures. Note that the common stocks have a -24% correlation with the commodity futures. Previously, we showed that combining two portfolios with a zero correlation reduced the variance of the portfolio. This was referred to as diversification. The common stocks and futures have negative correlation. This suggests that holding both in a portfolio will produce a portfolio variance that is less than the variance of the individual components.
Let's calculate the portfolio means and standard deviations. The two formulas that are relevant are:
and
We are given that for asset 1, the common stocks:
Also, asset 2, the commodity futures:
We are also given the correlation coefficient and the variances can easily be calculated:
The next step is to calculate the portfolio mean and standard deviation for various weights.
The mean return is:
E_p= 1 x 13.05 + 0 x 13.83= 13.05%
The standard deviation is:
STD_p=sqrt{(1 x .0359) + (0 x .0503) + (2 x 1 x 0 x -.24 x .1895 x .2243)}
=sqrt{.0359} = .1895 = 18.95%
E_p= .8 x 13.05 + .2 x 13.83= 13.21%
The standard deviation is:
STD_p=sqrt{(.64 x .0359) + (.04 x .0503) + (2 x .8 x .2 x -.24 x .1895 x .2243)}
=sqrt{.0217} = .1474 = 14.74%
E_p= .6 x 13.05 + .4 x 13.83= 13.36%
The standard deviation is:
STD_p=sqrt{(.36 x .0359) + (.16 x .0503) + (2 x .6 x .4 x -.24 x .1895 x .2243)}
=sqrt{.0161} = .1268 = 12.68%
E_p= .4 x 13.05 + .6 x 13.83= 13.52%
The standard deviation is:
STD_p=sqrt{(.16 x .0359) + (.36 x .0503) + (2 x .4 x .6 x -.24 x .1895 x .2243)}
=sqrt{.0190} = .1377 = 13.77%
E_p= .2 x 13.05 + .8 x 13.83= 13.67%
The standard deviation is:
STD_p=sqrt{(.04 x .0359) + (.64 x .0503) + (2 x .2 x .8 x -.24 x .1895 x .2243)}
=sqrt{.0304} = .1743 = 17.43%
STD_p=sqrt{(0 x .0359) + (1 x .0503) + (2 x 0 x 1 x -.24 x .1895 x .2243)}
=sqrt{.0503} = .2243 = 22.43%
These calculations verify the numbers presented in table 7.
TABLE 7 Nominal Rates of Return on Selected Common Stock-Commodity Futures Portfolios, 1950-76
Proportion of Portfolio Invested in Stocks
Year 100% 80% 60% 40% 20% 0
1950 31.71% 35.89% 40.07% 44.25% 48.43% 52.61% 1951 24.2 24.56 25.10 25.64 26.17 26.71 1952 18.37 14.45 10.53 6.62 2.70 -1.22 1953 -0.99 -2.06 -3.12 -4.19 -5.26 -6.32 1954 52.62 45.07 37.52 29.98 22.43 14.88 1955 31.56 24.29 17.02 9.75 2.48 -4.79 1956 6.56 8.20 9.84 11.47 13.11 14.75 1957 -10.78 -9.09 -7.40 -5.72 -4.03 -2.34 1958 43.36 34.42 Z5.48 16.55 7.61 -1.33 1959 11.95 9.67 7.39 5.11 2.82 0.54
Year 100% 80% 60% 40% 20% 0
1960 0.47 0.36 0.24 0.13 0.02 -0.09 1961 26.89 21.82 16.75 11.68 6.62 1.55 1962 -8.73 -6.81 -4.89 -2.97 -1.05 0.87 1963 22.80 22.81 22.81 22.82 22.83 22.84 1964 16.48 15.61 14.75 13.87 13.00 12.13 1965 12.45 12.08 11.72 11.35 10.99 10.62 1966 -10.06 -5.12 -0.18 4.76 9.71 14.65 1967 23.98 20.01 16.04 12.07 8.10 4.13 1968 11.06 9.10 7.13 5.17 3.20 1.24 1969 -8.50 -2.63 3.24 9.11 14.98 20.84
Year 100% 80% 60% 40% 20% 0
1970 4.01 5.61 7.20 8.80 10.39 11.99 1971 14.31 17.11 9.91 7.71 5.31 3.31 1972 18.98 21.93 24.87 27.82 30.76 33.71 1973 -14.66 8.53 31.82 53.06 78.30 101.54 1974 -26.48 -14.79 -3.10 8.58 20.27 31.98 1975 37.20 28.96 20.72 12.47 4.Z3 -4.01 1976 23.84 21.62 19.40 17.18 14.96 12.75
Year 100% 80% 60% 40% 20% 0
Mean 13.05 13.21 13.36 13.52 13.67 13.83 StdDev 18.95 14.74 12.68 13.77 17.43 22.43

Note that for the negative correlation the amount invested in the component securities has a large effect on the portfolio variance.
The next item is to look at the effect of different levels of correlations on the portfolio variance. Let's develop a better grasp of where these portfolios should lie in the mean-standard deviation space. In order to do this, assume that there are only two securities, q and s. The expected return on the portfolio is:
E_p= wE_q + (1-w)E_s
The standard deviation on the portfolio is:
STD_p= sqrt{w^2 x V_q + (1-w)^2V_s + [2 x w x (1-w) x V_qs]
Write this in terms of the correlation coefficient.
STD_p= sqrt{w^2 x V_q + (1-w)^2V_s + [2 x w x (1-w) x Corr_qs x STD_q x STD_s]
So now we can start to map out the frontier.

Consider a number of simple cases. First, if the correlation between the two securities is one, then the standard deviation on the portfolio is:
STD_p= | w x STD_q + (1-w)x STD_s |This result has a simple geometric interpretation (Click here to see the graph again). If we plot the mean and standard deviation of the two securities, then a straight line between the two securities represents the set of portfolios available. The point q below represents the situation where w=1 where as the point s represents the situation where w=0. Note that diversification when the correlation between the securities is one is ineffective.
The second straightforward situation is when the correlation between the two securities is negative one. The standard deviation of the portfolio is:
STD_p= | w x STD_q - (1-w) x STD_s |
This immediately implies that we can drive the standard deviation of the portfolio to zero by choosing the right weights. Setting the left-hand side equal to zero, we can solve for w:
STD_s
w = -------------
STD_q + STD_s
This point corresponds to the point y on the diagram.
Now let's consider the weights w. There is no restriction on the sign of w. Therefore, a negative w can be considered a short sale of security q. The dotted line extension of the lines in the figure represent short sales. Note that you can change the perfect positive correlation into negative correlation with the short sale provision.
More realistically, the correlation between the securities will between positive one and negative one. The curve on the diagram plots the possible portfolios with a correlation between zero and one.
Notice that any part of the curve that has a positive slope must be concave. Consider the counter example between u and v on the diagram. With a dashed line, I have drawn a convex segment. Is this a possible frontier? It turns out that the answer is no. We can consider u and v as separate portfolios of q and s. We know that the most extreme situation (farthest to the right) would be a correlation of positive one between these two portfolios. Hence, it is impossible to have any curve to the right of the straight line extreme case. So the frontier will be concave for all positive slopes.
Now lets be more precise. We have defined the mean-variance frontier. After plotting all the portfolio combinations, the points farthest the left are minimum variance. But consumers will only care about a certain portion of the frontier -- the portion with a positive slope. The negatively sloped part of the frontier implies a lower return for greater standard deviation. Our investors will not buy that trade-off. The positively sloped portion is called the efficient frontier. Portfolios on this frontier are referred to as mean--variance efficient. These portfolios maximize the expected return on the portfolio for a given variance. So there are dual properties of efficient portfolios:
These properties are reflected in all the portfolios in the efficient frontier. On the next page the opportunity set for investors is provided. Because of our assumptions about investors, only the positively sloping portion of the minimum variance curve is held. The solid line represents the efficient frontier. Note that I have also included arrows representing the direction of the investors' preferences (more return and less risk).


We have talked about efficient portfolios being determined by the investors' preferences for more return to less return and less risk to more risk. Now let's consider individual investors. All investors are assumed to be risk averse and like more to less. On the following page the efficient frontier is drawn and a set of indifference curves for an investor. The optimal portfolio for this particular investor is at the point of tangency between the indifference curve and the efficient frontier. [Note that the indifference curves can never be tangent to the inefficient portion of the frontier].

This is the optimal portfolio for one particular individual. Another person may be less tolerant of risk or very risk averse. This person's indifference curves are drawn below. Note that the optimal portfolio for this person has the smallest possible standard deviation.

The next graphshows a set of indifference curves for a person that has high risk tolerance or low risk aversion. Note that this does not mean that the person is a risk lover. The utility function is still concave (risk aversion) but it is close to linear for very low risk aversion. The tangency point on the indifference map shows this person choosing an efficient portfolio that has a large standard deviation compared to the other portfolios but note that the expected return is also higher.

Now consider the introduction of a riskless security like a Treasury bill. Suppose we invest in a combination of a portfolio on the efficient set (derived without the riskless security) and the riskless security. We can calculate the expected return and the standard deviation on this new portfolio.
E_p = (1-w) x R_f + w x E_e
STD_p = w x STD_e
Where R_f represents the risk free security, E_e represents
the portfolio on the efficient frontier and w is the proportion
of funds invested in the risky security.
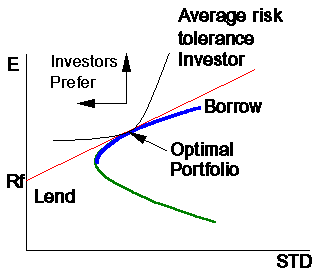
It is clear that the only portfolio on the old efficient frontier that is desirable is the tangency portfolio. If we chose another portfolio like A or B, this opportunity set is not efficient because for a given variance, you do not maximize the expected return.

Now, I mentioned the old efficient frontier and it is time to clarify what this means. By introducing a new security, the riskfree security, we have to redraw the efficient set. It turns out that the new efficient set is the straight line from the riskfree rate to the tangency portfolio and beyond. If you are on the line to the right of the tangency portfolio, you are borrowing at the riskfree rate (note we are assuming that borrowing and lending rates are the same) and investing in the tangency portfolio. If you are at the point R_f on the y-axis, this means that you have none your money (w=0) in the risky asset. If you are at the point M, then all of your money is in the portfolio of risky assets (w=1) -- which is the tangency portfolio. The line that forms this new efficient set is called the Capital Market Line.
So with a risky asset, there is only one optimal combination of risky investments for each investor. Diagrams are provided that show the optimal portfolio choice for individuals of average, low and high risk tolerance. The optimal portfolio is the tangency of the indifference curve to the efficient set.


If all investors agree upon E, V and R_f then that optimal risky asset mix is the same for all (and must be the market portfolio). This is a fundamental point and provides the basis for the asset pricing theory. The implication is that only two funds are held by every investor: a fund comprised of the riskfree instrument and a fund which is the market portfolio. We call this the 2 fund theorem. If people agree on the expected returns and variance-covariance matrix, then they will see the same efficient frontier. With the riskfree asset, there is only one portfolio of risky assets that is efficient. This does not mean that the only investment portfolio that is held is M. We know that people have differing degrees of risk aversion. What is implied that there is only one portfolio of risky assets held in conjunction with the riskfree asset. This portfolio of risky assets is the value weighted market portfolio.
Consider investment in a riskless asset with a return of R_f and standard deviation of zero and a risky asset with mean return of E and standard deviation of STD. Let the portfolio weight for the risky asset be w and the portfolio weight for the riskfree asset must be 1-w. Now let's calculate the portfolio mean and standard deviation. We know the formula for the portfolio mean for two assets is:
E_p = (1-w) x R_f + w x E
STD_p = w x STD
We can also write the expected returns equation as:
E_p = R_f + w x [E - R_f]
But we know from the standard deviation equation:
STD_p
w = -----
STD
Substitute this formula for w into the expected returns
equation.
E - R_f
E_p = R_f + (-------) STD_p
STD
The term
E - R_f
(-------)
STD
is called the Sharpe Measure [Named after William Sharpe.]
It is used to evaluate
investments. Below is a graph depicting the expected return--standard deviation
space. The Sharpe measure is the slope of the line from R_f
(rise is E-R_f over
run which is STD). The intercept is the riskfree rate, R_f.

The higher the Sharpe measure is the better the security looks. On the graph we could combine a strategy of borrowing and buying portfolio A to achieve the same expected return as portfolio B with a much smaller variance.
Let's consider a specific example. Suppose R_f=.08, E_A=.20, STD_A=.20, E_B=.25 and STD_B=.30. Just looking at portfolio A and B it is unclear which is the best investment. B has the higher return -- but it also has a higher variance. Let's first consider the Sharpe measures:
E_A - R_f .20 - .08
S_A = --------- = --------- = .60
STD_A .20
E_B - R_f .25 - .08
S_B = --------- = --------- = .56
STD_B .30
The measure suggests that portfolio B is dominated by a strategy of borrowing and holding portfolio A. Let's check this out by calculating the standard deviation of a levered portfolio of A that has exactly the same expected return as B:
.25 = w x .20 + (1-w) x .08
Solving for w weight:
w = .17/.12 = 1.4167
This suggests that a strategy of investing 141.67% of your money
in A and borrowing 41.67% at the rate of R_f=.08 will deliver
a portfolio return of 25% which is exactly the portfolio return
for B. Now lets check the standard deviation of this levered
portfolio:
STD_p = sqrt{(1.4167)^2 x (.20)^2} = 28.33%
Note that the other terms in the portfolio variance drop out because
the variance of the riskfree asset is zero. We are left with
a portfolio standard deviation of 28.33% which is lower than
the 30% for portfolio B. The levered portfolio that contains
A has the same mean as B but a lower standard deviation.
As a result, the levered portfolio with A is preferred to the investment in
B.
We can expand the analysis to include the all asset available in the market. We showed last time that only the positively sloped portion of the minimum variance frontier of risky assets satisfied our portfolio selection rules. Now let's introduce the riskfree asset into the analysis. We can use the tools that we developed above the discriminate among the portfolios on the efficient frontier of risky assets. We will search for combination of the riskfree asset and some risky portfolio that delivers the highest Sharpe measure. We know that the Sharpe measure is just the slope of the line that is drawn from the riskfree rate on the expected return axis. The portfolio with the highest Sharpe measure is the tangency portfolio.
So the best possible mean and standard deviation combinations are from the riskless and tangency portfolio. If 100% of your wealth is invested in the riskless asset, then you return is R_f and the standard deviation is zero. If 50% of your wealth is invested in the riskless asset and 50% of your wealth is in the tangency portfolio, then your portfolio lies in between R_f and M on the straight line. If 100% of your money is in the tangency portfolio, the your expected return is the expected return on the tangency portfolio and your standard deviation is the standard deviation on the tangency portfolio. Finally, if you borrow money at the riskless rate and combine your borrowing with your initial wealth to buy the tangency portfolio, then your portfolio is to the right of M on the straight line. This straight line is called the Capital Market Line.
Since total lending equals total borrowing in the economy, the tangency portfolio is the market portfolio. The market portfolio represents total invested wealth in risky assets. It is a portfolio with weights defined to be the total value of the asset divided by the total value of all risky assets. These weights are referred to as value weights.

Before we solve the planning problem, we know what the solution will look like from our geometric analysis. People will hold the riskfree assets and a portion of the market portfolio of risky assets. But this insight does not tell us much about the risk of individual securities -- it just tells us what is held in equilibrium.
First, let's consider some of the data and assumptions that we need to solve the portfolio selection problem. First, we need to collect expected returns on all assets E. Second, we need to collect the variances and covariances of all assets' returns V. With these data, we can construct the minimum variance frontier and the efficient frontier of all risky assets (positively sloped portion of the minimum variance frontier). Third, we need riskless borrowing and lending at the rate R_f. With this additional data, we can construct the capital market line. This line will describe all the efficient portfolios that are a combination of two funds: the riskless asset and the tangency portfolio. The final step has to do with individuals' beliefs about the means and standard deviations of the assets' returns. If there is complete agreement or homogeneous expectations, then all investors will agree on the means and standard deviations. This implies that they all see the same efficient frontier of risky assets and they will all see the same capital market line once the riskless asset is introduced.
A critical ingredient is that the expected returns, volatilities and covariances must be expected. When I say "collect" these variables, this is an involved process relating to forecasting. It is unlikely that historical averages will be appropriate forecasts of the future. This forecasting task is the topic of Global Tactical Asset Allocation.
The Appendix section to this lecture details the derivation of the planning problem. The results are stated in this section without proof. Before the results are stated, we have to review some definitions.

The problem is to minimize portfolio variance subject to two constraints. The first constraint sets the level of expected return. Remember part of our definition of an efficient portfolio stated that you minimized variance for a given level of expected return. The first constraint sets this "given" level of expected return. The second constraint makes sure that the sum of the portfolio weights, w, is one. When this problem is solved, the efficient frontier portfolio weights are:

where lambda_1 and lambda_2 are Lagrangian multipliers. By varying these multipliers, the entire efficient frontier of risky assets is traced out.
The optimal combination of risky assets or the tangency portfolio can be found as:

Note that the sum of the portfolio weights w'1 equals one.
The capital market line can also be derived. Define:

With this definition, the capital market line is:

That is, with various values of sigma (portfolio standard deviation), a straight line is traced in mean-standard deviation space originating at R_f. A proof is found in Ingersoll, Theory of Financial Decision Making (1987, p.89).
The quadratic programming problem is the following:

The lambda_1 and lambda_2 terms are Lagrangian multipliers. The first order necessary conditions result from differentiating with respect to the portfolio weights:

Solving for expected return:

This means that the expected return for any security is linear in its covariance with all the other securities. We can also solve the first order conditions for the optimal weights:

The next step would be to solve for the Lagrangian multipliers. This is done by considering the constraints as a set of two equations and solving for the unknown multipliers after we substitute the above expression for the optimal weights into the first order conditions.
The optimal combination of risky assets (the tangency portfolio) is

Note that the weights sum to one.
The capital market line can also be derived. Define

With this definition, the capital market line is:

That is, with the various values of the portfolio standard deviation (sigma), a straight line is traced in mean-standard deviation space originating at r_f.
Much of the material for this lecture is drawn from Douglas Breeden, "Portfolio Statistics".}