
Copyright 1995 by Campbell R. Harvey. All rights reserved. No part of this lecture may be reproduced without the permission of the author.
Revised: November 16, 1995
WWWFinance provides links to a sample contract quotation, the contract specifications and some general information about many of these contracts. When browsing through these quotations, note that the average dollar volume on the New York Stock Exchange is about $5 billion a day. In comparison, the Eurodollar contract (traded on the Chicago Mercantile Exchange) trades on average 400,000 contracts per day. Each contract represents a $1 million dollar certificate of deposit in a London bank. The dollar volume is $400 billion.
There has been remarkable growth in the futures market. Most of this growth has come from the financial futures. Note that the leading contracts are the Treasury bond futures (CBOT) and the Eurodollar futures (CME). In addition, there has been significant growth international futures markets. There are a number of reasons for this growth.
The next few sections are drawn from Douglas Breeden, "Some Common Misconceptions about Futures Trading."
One of the most common mistakes that a small investor makes in futures trading is considering the margin on the futures contract as the investment. Margin is a deposit -- usually 5--10% of the contract's value -- required by the futures exchange from both the buyer and the seller of the contract. Margin helps to ensure that both buyer and seller will perform as specified in the futures contract.
It is best to look at an example. This historical example is taken from the early 1980's - a period of unprecedented interest rate swings. In May 1981, the initial margin required by the Chicago Board of Trade from both buyers (longs) and sellers (shorts) of U.S. Treasury bond futures contracts was $4,000 per contract. A June futures contract calls for delivery of a Treasury bonds with a face value of $100,000 and a current market value of approximately $65,000. The margin required is about 6% of the value of the contract. Furthermore, the exchange stipulates that a margin balance of at least $3,000 per contract be maintained at all times.
If on the first day after a trade was made, the futures price falls from 65.00 per $100 face to 64.50, the buyer or long loses $500 ($0.50 x 1000) and the seller or short gains $500. This amount is actually transferred by the buyer's broker to the seller's broker. The seller can take the $500 out of his brokerage account and use it in other investments if he so desires. The buyer in the futures contract has his brokerage account debited for $500, leaving an account equity of $3,500. Since this is in excess of the $3,000 minimum maintenance margin required by the exchange, no additional margin need to be posted. In exchange for the $500, the futures contract that was initiated at a price of 65.00 is automatically rewritten by the exchange to specify delivery at a price of 64.50, the current market price for that contract. By this process of marking to market, all futures contracts for the same commodity and delivery date specify the same delivery price, making them identical contracts.
Now consider what happens the next day. The June Treasury bond contract falls from 64.50 to 63.50. The long has a loss that day of $1,000. which is the short's gain. After the contract is rewritten with a price of 63.50 and the $1000 is transferred from the long to the short, the long's equity drops to $2,500. As this is below the $3,000 maintenance margin required by the exchange, the long receives a margin call from his broker. The long must deposit $1,500 to raise his account balance to the initial margin level of $4,000. Thus, in this example, the buyer has had to deposit a total of $5,500 with his broker so far. Clearly, the initial amount of $4,000 is not the total at-risk investment required to take and hold a Treasury bond futures contract.
Table 1 shows the cash flows for the long position from April 1 to May 29.
| Date | June 1981 T-bond Futures Price |
Daily Gain or Loss | Account Balance | Margin Deposit | New Account Balance |
Total Deposit | Total Profit or Loss |
|---|---|---|---|---|---|---|---|
| 4/1/81 | 67.03 | - | 0 | $4,000 | $4,000 | $4,000 | 0 |
| 2 | 66.19 | -840 | $3,160 | 0 | 3,160 | 4,000 | -840 |
| 3 | 65.56 | -630 | 2,530 | 1,470 | 4,000 | 5,470 | -1,470 |
| 6 | 63.34 | -1,720 | 2,280 | 1,720 | 4,000 | 7,190 | -3,190 |
| 7 | 65.38 | +1,340 | 5,540 | 0 | 5,540 | 7,190 | -1,650 |
| 8 | 64.50 | -880 | 4,660 | 0 | 4,660 | 7,190 | -2,530 |
| 9 | 65.25 | +750 | 5,410 | 0 | 5,410 | 7,190 | -1,780 |
| 10 | 64.50 | -750 | 4,660 | 0 | 4,660 | 7,190 | -2,530 |
| 13 | 64.19 | -310 | 4,350 | 0 | 4,350 | 7,190 | -2,840 |
| 14 | 64.69 | +500 | 4,850 | 0 | 4,850 | 7,190 | -2,340 |
| 15 | 63.78 | -910 | 3,940 | 0 | 3,940 | 7,190 | -3,250 |
| 16 | 63.53 | -250 | 3,690 | 0 | 3,690 | 7,190 | -3,500 |
| 20 | 64.50 | +970 | 4,660 | 0 | 4,660 | 7,190 | -2,530 |
| 21 | 64.16 | -340 | 4,320 | 0 | 4,320 | 7,190 | -2,870 |
| 22 | 63.97 | -190 | 4,130 | 0 | 4,130 | 7,190 | -3,060 |
| 23 | 63.88 | -90 | 4,040 | 0 | 4,040 | 7,190 | -3,150 |
| 24 | 63.50 | -380 | 3,660 | 0 | 3,660 | 7,190 | -3,530 |
| 27 | 63.28 | -220 | 3,440 | 0 | 3,440 | 7,190 | -3,750 |
| 28 | 63.38 | +100 | 3,540 | 0 | 3,540 | 7,190 | -3,650 |
| 29 | 62.56 | -820 | 2,720 | 1,280 | 4,000 | 8,470 | -4,470 |
| 30 | 61.88 | -680 | 3,320 | 0 | 3,320 | 8,470 | -5,150 |
| 5/1/81 | 62.31 | +430 | 3,750 | 0 | 3,750 | 8,470 | -4,720 |
| 4 | 60.41 | -1,900 | 1,850 | 2,150 | 4,000 | 10,620 | -6,620 |
| 5 | 59.97 | -440 | 3,560 | 0 | 3,560 | 10,620 | -7,060 |
| 6 | 60.38 | +410 | 3,970 | 0 | 3,970 | 10,620 | -6,650 |
| 7 | 61.63 | +1,250 | 5,220 | 0 | 5,220 | 10,620 | -5,400 |
| 8 | 61.75 | +120 | 5,340 | 0 | 5,340 | 10,620 | -5,260 |
| 11 | 60.31 | -940 | 4,400 | 0 | 4,400 | 10,620 | -6,220 |
| 12 | 60.75 | -160 | 4,340 | 0 | 4,340 | 10,620 | -6,280 |
| 13 | 60.69 | -60 | 4,280 | 0 | 4,280 | 10,620 | -6,340 |
| 14 | 62.25 | +1,560 | 5,840 | 0 | 5,840 | 10,620 | -4,780 |
| 15 | 62.41 | +160 | 6.000 | 0 | 6,000 | 10,620 | -4,620 |
| 18 | 63.84 | +1,430 | 7,430 | 0 | 7,430 | 10,620 | -3,190 |
| 19 | 62.97 | -870 | 6,560 | 0 | 6,560 | 10,620 | -4,060 |
| 20 | 63.19 | +220 | 6,780 | 0 | 6,780 | 10,620 | -3,840 |
| 21 | 62.39 | -600 | 6,180 | 0 | 6,180 | 10,620 | -4,440 |
| 22 | 63.50 | +910 | 7,090 | 0 | 7,090 | 10,620 | -3,530 |
| 26 | 64.09 | +590 | 7,640 | 0 | 7,640 | 10,620 | -2,980 |
| 27 | 63.91 | -180 | 7,480 | 0 | 7,480 | 10,620 | -3,140 |
| 28 | 64.69 | +780 | 8,260 | 0 | 8,260 | 10,620 | -2,360 |
| 29 | 64.75 | +60 | 8,320 | 0 | 8,320 | 10,620 | -2300 |
We usually think of an investment as a negative cash flow today for some future expected return on that initial cash flow. Futures is a little complicated because the only cash flow out today is the margin. In fact, large clients are allowed to keep their margin in Treasury bills -- so it is hard to see any cash outflow today. The best way to view the investment in a futures contract is to treat the investment as if the entire value of the contract were placed in Treasury bills or a money market fund at the inception of the contract. As margin is needed, funds are simple transferred out of the money market fund and into your commodities account. Excess margin is transferred back into the money market fund to earn interest. In the Treasury bond futures example in Table 1, this would mean that the investment should be viewed on April 1 as $67,020 in June Treasury bonds. The return on this investment has two components: (1) the interest earned on funds in the money market fund at rate r, and (2) the gain or loss on the futures contract expressed as a fraction of the total investment. The portfolio returns is

Most futures traders employ leverage by not setting aside the full value of the contract in a money market fund. Define leverage to equal to the ratio of the value of assets controlled to the value of funds set aside investment. For example, if $20,000 were set aside in a money market fund for the Treasury bond contract's assets worth $67,030, the leverage ratio would be:

From this equation, it is straightforward to compute the standard deviation of your return on equity from your leverage and the standard deviation of the percentage change in the futures prices:

Based on historical relationships, an equity amount equal to 5 to 8 times the margin required by the futures exchange results in a standard deviation of return on equity that is of approximately the same as the standard deviation of a typical stock (10% monthly). Of course, this is just a rule of thumb, but it does give some guidance on the funds that should be set aside in a money market fund for a futures contract.
For more information on margins, see Example Margin Tables .
Net Revenue(bond sale plus futures) = Q[B_T + (F_T - F_0)] =QF_0 + Q[B_T - F_T]
From the above equation, the net revenue from the hedge position is composed of (1) a certain component that depends upon the futures price at the time of the hedge (F_0) and (2) an uncertain component that depends upon the difference between the price received for bonds in the spot market and the futures price at closeout (B_T-F_T). The difference between the spot and the futures price is called the basis. Thus, uncertainty about the net hedged revenue arises if there is uncertainty about the basis. To quote Holbrook Working, "hedging is speculation in the basis".
There are many reasons for the basis to be uncertain.
There is no reason that the futures should be played in a high risk manner by a large investor. Of course, if the futures investor does not have enough capital (5--8 times margin), then he is required to play with considerable leverage or not at all. Before taking great leverage, the small investor should consider looking at a smaller contract (grain on CBT is 5,000 bushels whereas Mid-America contract is 1,000 bushels).
The effect of leverage on volatility can be seen from table 1. If a small investor is foolish enough to enter the contract with equity equal to the $4,000 margin, his loss is 176.5% by May 5 (7,060/4,000); borrowing of $6,620 are needed to sustain the position with only $4,000 in equity. However, the decline in the futures price was only 10.5% (59.97/67.03 - 1). Therefore, an investor who set $67,030 aside in a money market fund would have lost only 10.5% of his capital (actually less due to the interest earned). The difference in returns is due to the leverage employed by the first, $67,030/$4,000=16.8. Indeed, the levered loss (176.5% ignoring interest) is 16.8 times the unlevered loss of 10.5%. It is the leverage employed by futures traders that makes returns more volatile than stock returns.
Below graphs of the futures and options payoffs are provided. The graphs how that options payoffs are highly nonlinear or skewed relative to the underlying asset's price, whereas the futures payoffs are linear in the underlying asset's price. Of course, this does not mean that options are better or worse than futures. They are just different financial instruments. Due to their limited liability aspect, options are naturally levered and are often 3--10 (or more) times riskier than investing an equivalent amount of money in the underlying stock. With their linear payoffs, futures contracts are much more like buying stocks or bonds (possibly on margin) than they are like options.
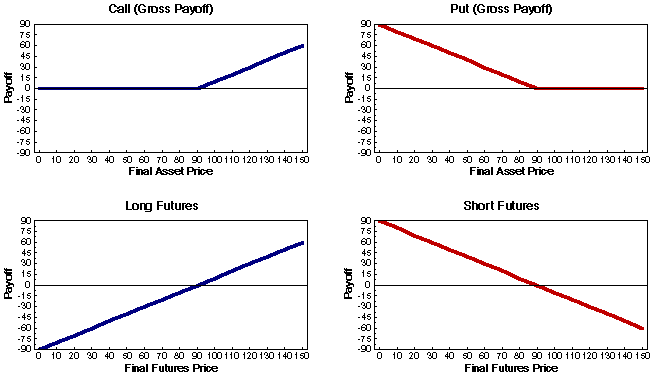
There are a number of important insights that should be reviewed. The first is that we should be careful about what we consider the investment in a futures contract. It is unlikely that the margin is the investment for most traders. It is rare that somebody plays the futures with a total equity equal to the margin. It is more common to invest some of your capital in a money market fund and draw money out of that account as you need it for margin and add to that account as you gain on the futures contract. It is also uncommon to put the full value of the underlying contract in the money market fund. It is more likely that the futures investor will put a portion of the value of the futures contract into a money market fund. The ratio of the value of the underlying contract to the equity invested in the money market fund is known as the leverage. The leverage is a key determinant of both the return on investment and on the volatility of the investment. The higher the leverage -- the more volatile are the returns on your portfolio of money market funds and futures. The most extreme leverage is to include no money in the money market fund -- only commit your margin.
The second important insight had to do with hedging with futures
contracts. The concept of basis risk was introduced. It is
extremely unlikely that you can create a perfect hedge. A perfect hedge
is when the loss on your cash position is exactly offset by the
gain in the futures position. We suggested some reasons why it is unlikely
that we can construct a perfect hedge.
Most of the applications that we will consider in finance center on the financial futures. In fact, the main focus will be on hedging with financial futures. The best way to understand hedging is to do some examples.
What exactly happened? The investment bankers were using T-Bonds and short term interest rate futures to hedge their holdings of mortgage backed securities. In the first part of 1986, interest rates dropped considerably. As interest rates drop, bond prices go up. So the firms were taking losses on their short futures position. Usually, with a hedged position, the losses on the short position are offset by gains in the financial instrument that you are holding. That is, if I was holding a corporate bond, as interest rates went down the bond price would go up and there would be gains in the cash position that offset the losses in the short position. With the mortgage backed securities, this did not occur. As rates dropped, people began to prepay their mortgages. Mortgage holders were exercising their call option with the exercise price of the par value of the mortgage plus the prepayment fee. As a result, the duration of the mortgage backed securities dropped and the price did not go up and in some cases the prices actually fell. So the investment bankers were faced with losses on the futures and losses in the cash. This is why Wall Street took such a bath in early 1986.
The purpose of the short hedge is to offset risk in a cash position. Consider the case of a bank with a $500 million holding of government securities. It is January 1, 1996. The bank investment committee expects a rise in the yield on government bonds within the next two months and a leveling off thereafter. That is, the investment committee expects a capital loss on the bank holdings of the government bonds (a rise in interest rates causes the bond prices to drop). You have recently been hired into the finance group. Your job is to set up a hedge.
To simplify this example, suppose the bank is holding 8% Treasury bonds with 20 years to maturity. The going rate in the market is 8.2%. So the bonds are worth approximately par value. The hedge will involve agreeing to sell Treasury bonds in the future. You call up your broker and sell 5000 March T-Bond contracts on the Chicago Board of Trade. The face value of the contract is
5000 x $100,000=$500,000,000.
Since the going rate in the market is close to the coupon on the underlying asset, the futures are trading close to par.
The next step is to follow the daily cash flows. If the bank's investment committee is correct and the rates go up, the value of the bonds that the bank holds will go down. At the same time on the futures side, you will be making money. As the rates go up, the settlement prices on the T-Bond futures will go down. Money will be transferred into your account. This money will help offset the losses on the cash market.
Since the investment committee believes that the rates will level off by March, you should execute a reversing trade in March -- or deliver your bonds. Since the bank wants to keep the Treasury bonds, buy 5000 March T-Bond contracts on March 1, 1996.
This was a very simple example. The hedge worked quite well because we were holding an instrument that was assumed to be the deliverable instrument. Note the T-Bond futures contract is a very good hedge against 8% 20 year bonds, it is not as good for other coupons. If the bank was holding $500 million in corporate bonds, the quality of the hedge would be determined by the correlation between changes in corporate yields and changes in the Treasury yields.
The last thing to realize is that if the rates went down, then you would make money on the cash side. Those gains, however, would be wiped out by losses on the futures side. So the hedge reduces both the downside and upside potential for your investment. Many portfolio managers do not use interest rate futures because of the limitation on the upside. Those managers that do use futures do not necessarily hedge 100% of the exposed assets like we did in this example. If you hedge 50% of your asset base, you cut the downside risk but still leave some upside potential.
The next example shows how a short hedge can be used to manage the liability side of the balance sheet. Suppose that a bank expecting to issue $100 million in one year certificates of deposits (CDs) three months from now is concerned with rising interest rates. In order to lock in today's CD rate, the bank could enter the following transactions:
Date Cash Market Futures Market
January 14 No transaction Sell 100 90-day June U.S. Tbill CD rate=9% on IMM (current settlement price = 92.00) Proceeds* = 100,000,000-(91/360x 8/100 x 100,000,000) = $97,977,778.00 April 5 Issue $100 million of Cover the short position (June Cds at 10%. Additional contract quoted at 90.00) annual interest costs = Costs = 100,000,000 -(91/360 x 10/100 x 100,000,000) = $97,472,223.00 Profit on the short position = 1/100 x 100,000,000= $97,977,778-$97,472,223 = $1,000,000 $505,555 *The funds are not actually received. In fact, the short seller would have to pay the margin requirement on the contracts. We use this concept to simplify the presentation.
This example shows why it is often difficult to learn finance from the textbook. What is wrong with this hedge? Should 200 contracts have been taken? Why?
This hedge is what I call the "naive hedge". Because $100 million in CDs are involved, the hedger elects to take a position in the futures market with underlying principal equal to $100 million. There is a major flaw in this logic. The size of the position (number of contracts taken should depend on the relative sensitivities of the cash position and the futures position to changes in interest rates. The Cds are 1 year to maturity. The hedging instrument is 3 months to maturity. A quick calculation of the modified duration shows that the CD is 4 times more interest rate sensitive than the T-bill. Actually, the correct hedge involves 400 contracts.
Date Cash Market Futures Market
January 14 No transaction. Average Buy 50 June T-bond futures contracts yield on long-term on the CBT. Settlement price = 76 bonds is 10.25% 10/32. This price is based on the delivery of an 8% coupon bond. Assuming that such a bond is available and cheapest to deliver, the cost of 50 contracts is 50x.763125x$100,000=$3,815,625 (The pension fund manager is only obli- gated to pay the margin requirement per contract and is expected to be ready to meet the margin calls.) The cost is the financial committment required if the manager takes delivery of the bonds when the futures contract matures. April 5 Invest $5 million at 9.5%. Sell 50 June T-bonds futures contracts Opporunity lost = 0.75% at 80. The proceeds are = or 0.0075x$5,000,000 = 50x$100,000x0.80=$4,000,000 $37,500 This opportunity loss will be Profits = $4,000,000 incurred over the life of the -3,815,625 investment, which can well =$184,375 exceed a year in the case of the pension fund.* *Assuming a 20 year time horizon, we can work out the present value by multiplying $37,500 times the annuity factor for 10.25% which is 8.4. Hence, the present value is $315,000.
What is wrong with this hedge? Obviously, the loss exceeds the gain on the hedge. But why? This is also another example of the naive hedge. There is no reference to interest rate sensitivity. However, there is even a more serious problem. Why hedge $5 million in bonds with $3.8 million in futures (even assuming the modified durations are identical)? This is what I call the 'double naive hedge'. The person doing the hedging has confused principal value with the market value. We always hedge using market value.