![]()
Copyright 1997 by Campbell R. Harvey and Stephen Gray. All rights reserved. No part of this lecture may be reproduced without the permission of the authors.
Latest Revision: July 2001
8.0 Overview
This class extends the diversification material in deriving the Capital Asset Pricing Model (CAPM). This model is widely used in capital budgeting exercises in practice and is one of the cornerstones of modern finance. The primary use of the CAPM is in determining the appropriate discount rate to use in computing Net Present Values (NPVs). This module, highlights the difference between systematic risk (which is priced or rewarded by investors) and diversifiable risk (which is not awarded). An intuitive proof is presented along with a formal mathematical proof.
8.1 Objectives
Show that in large diversified portfolios an individual assetís contribution to the risk of the portfolio is its covariance with the returns of the existing portfolio and that individual variances are irrelevant.
8.2 The Derivation of the CAPM
In a world with all the assumptions made so far, all individuals should hold the market portfolio levered up or down according to their degree of risk tolerance. A person with low risk tolerance (high risk aversion) will have most of her money in the riskfree security while a person with high risk tolerance (low risk aversion) will borrow to finance the purchase of the market portfolio.
For an individual at her optimum portfolio, consider a small additional borrowing to finance the purchase of asset i.
|
Portfolio |
Market |
Asset i |
Riskless |
|
Optimum |
wm = 1 |
wi = 0 |
0 |
|
Candidate |
wm = 1 |
wi = D |
-D |
Let's consider the mean and variance of the optimal portfolio.
![]()
Next consider the derivative of the portfolio variance with respect to the weight in asset i:

At the optimum, we know that wm = 1 and wi = 0. So let's evaluate this derivative at these points:

Next consider the derivative of the expected portfolio return with respect to the weight in asset i:

At the optimum, the marginal change in portfolio expected return per unit of change in the variance must be equal for all securities (and the market portfolio m). The idea is the following. The ratio of incremental return to risk must be the same across all assets. Suppose it is not, Asset A has higher expected return per unit of contribution of risk than Asset B. People will sell their B and buy A. A's price is bid up and B's price is bid down. As A's price goes up, the expected return decreases. As B's price goes down, the B's expected return increases. This is risk arbitrage. This will occur until everything is equalized. This implies:

Cross multiplying yields:
![]()
This is the Capital Asset Pricing Model (CAPM) which was developed by William Sharpe in 1964 (Click Here to go to Sharpe's home page).
Substituting beta for the ratio of the covariance to the variance, we have the familiar form:
![]()
which holds for all assets i.
In this section, we sketch an intuitive proof of the CAPM which ties together the fundamental economic ideas of utility theory and the concept of diversification using some basic statistics. The contribution of each of these building blocks is outlined in turn below.
8.4 Fundamental Economics/Utility Theory
From the fundamental economic idea of utility theory covered in the diversification lecture, we established that
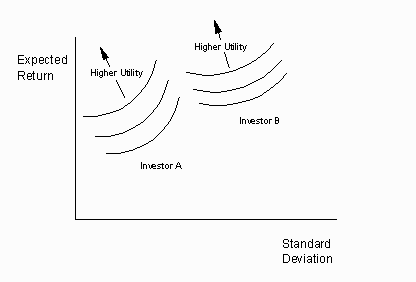
The ideas both seem quite reasonable. The figure below shows two sets of utility curves that satisfy these two requirements. Although both investors are risk averse, investor A is more tolerant of risk than is investor B.
In the diversification lecture, for simplicity, we dealt with an investor considering a single investment which either made a particular profit or a particular loss. In what follows, we generalize this argument to consider:
8.5 Diversification
We have established above that investors are risk averse and prefer high returns. Therefore, they will adopt any strategy that allows them to decrease risk without decreasing expected returns. We saw earlier that diversification is such a strategy. Therefore, we conclude that all investors will seek to hold diversified portfolios.
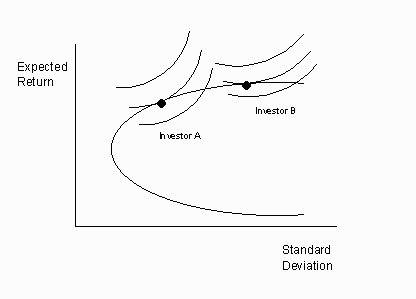
For a graphical interpretation of this argument, consider the following diagram of the investment opportunity set. This is the set that encompasses all risky assets (those that do not have a certain guaranteed return) and all portfolios of risky assets. Also marked on the graph are the portfolio choices of investors A and B from above. Note that investor B, who is more tolerant toward risk, chooses a portfolio with higher risk and higher expected return than that chose by investor A.
Next, suppose that there exists a riskless asset - one that has a certain,
guaranteed return of rf. This asset can be thought of
as a short-term Treasury bill. Also assume that investors can borrow and
lend at this riskless rate, rf.. Consider a portfolio
P consisting of a proportion in the riskless asset and (1-a) proportion
invested in a portfolio of risky assets M that has expected return E[rm]
and standard deviation ![]() . The resulting
portfolio has expected return
. The resulting
portfolio has expected return ![]()
![]()
and variance
![]()
since rf is a constant (i.e., the variance of a constant is zero and the covariance of a constant and a random variable also equals zero). Therefore, the standard deviation of the returns of portfolio P has a convenient linear form:
![]()
8.6 The Investment Opportunity Set with a Riskless Asset
Depending on the proportion invested in the riskless asset, the resulting portfolio lies somewhere on a straight line joining the two components in expected return-standard deviation space. This is illustrated in the following figure for the case where M happens to be the tangency portfolio.

Clearly, an investment in this portfolio M (the tangency portfolio) and the riskless asset is an optimal strategy for all investors. Investors will only differ in the relative proportions invested in the two components. The next figure illustrates that both investor A and investor B will prefer this strategy to an investment in risky assets alone. Investor A, who is more averse towards risk, invests a higher proportion of his wealth in the riskless asset than does investor B. From the figure, investor A invests about half his wealth in the riskless asset and half in the portfolio of risky assets M. Investor B invests all his wealth in the portfolio of risky assets M, then borrows at the riskless rate, rf, and invests this in the portfolio of risky assets as well.

The equation to this line which represents the possible sets of portfolios of the riskless asset and portfolio M is

where rf is the intercept and  is the slope of the line. We could also write
is the slope of the line. We could also write
![]()
Note, however, that for a portfolio to be on this line, it must be perfectly positively correlated with M (i.e., rho(p,m) = 1). Intuitively, this is because these portfolios are composed of the riskless asset and portfolio M, so the only source of variation in the portfolios returns is variation in the returns of portfolio M. Mathematically we can see that this is the case by definition.

Therefore, this line is only informative about assets and portfolios whose returns are perfectly positively correlated with those of portfolio M. The contrast between these assets and those that are not perfectly positively correlated with M is highlighted in Figure 5 which plots the Capital Market Line (CML).

This figure shows why assets that are not perfectly correlated with M do not fall on the CML by using an investment in IBM stock as an example. The figure shows that there are two ways to receive an expected return of E[rIBM]: simply buy shares in IBM, or buy portfolio A. For a risk averse investor (as we all are) portfolio A is preferred to an investment solely in IBM since it produces the same return with less risk. It is impossible to earn an expected return of E[rIBM] incurring less risk than that of portfolio A. The total risk of IBM can therefore be decomposed into systematic risk, the minimum risk required to earn that expected return and diversifiable risk, that portion of the risk that can be eliminated, without sacrificing any expected return , simply by diversifying. Investors are rewarded for bearing this systematic risk, but they are not rewarded for bearing diversifiable risk, because it can easily be eliminated at no cost.
8.7 Finding the Market Portfolio and Measuring Systematic Risk
Two questions remain: (1) What is this portfolio M? and (2) How do we measure this systematic risk? Each of these questions is explored below.
Since all investors will want to hold the same portfolio of risky assets (M, the tangency portfolio) and since all risky assets must be owned by investors, the conclusion is that all investors will hold the market portfolio (the portfolio of all risky assets) in some proportion. This is the key implication of the Capital Asset Pricing Model. Note that this conclusion is consistent with investors seeking to maximize the benefits of diversification by continuing to diversify until there are no assets left to diversify across. That is, they spread their wealth across all assets that are available investments so that all investors hold the market portfolio, in some proportion (Note that all of the mathematical results and the intuition also go through so long as investors hold well-diversified portfolios. That is, the model is still valid even if not all investors hold the whole market, so long as all investors are well diversified).
Now, given that investors hold diversified portfolios, how do we measure the risk and return of an investorís portfolio? For ease of exposition, suppose that an investor has formed an equally-weighted portfolio of n assets. That is, he has invested 1/n proportion of his wealth in each of n different assets. From the diversification lecture, we know that the expected return of such a portfolio is given by:
![]()
and that the variance of the returns of such a portfolio is given by:
![]()
Further, recall that for a portfolio of n assets there are:
so the equation above reduces to
![]()
Now, as n becomes large (say n goes to infinity), the
variance of the portfolio approaches the average covariance (![]() goes to Average Covariance) because the first term, 1/n,
gets close to zero and the second term n2/n2-1/n
gets close to one. That is, the variance of a large portfolio is simply
the average covariance of the individual stocks.
goes to Average Covariance) because the first term, 1/n,
gets close to zero and the second term n2/n2-1/n
gets close to one. That is, the variance of a large portfolio is simply
the average covariance of the individual stocks.
| Example 8.8
Consider again the following example from the diversification lecture. Suppose that we consider forming equally weighted portfolios from securities, all of whose expected rates of return (Ei) are 20 percent, whose standard deviations of rates of return are 20% and the correlation between the returns of any two securities (ri,j) is 0.5. The expected portfolio return and the standard deviation of the portfolio return appeared as follows as we increased the number of securities in the portfolio:
The equation above tells us how this table was created. In addition,
we now know that the variance of the portfolio is converging (as n goes
to infinity) to the average covariance between the assets. Since covariance
is given by |
8.9 Risk in a Portfolio Sense
We now consider an investor who holds a widely diversified portfolio and is considering adding a new asset to his portfolio. How will this new asset affect the risk of this portfolio? We have established above that the variance of the portfolio will be the average covariance between all of the assets in the portfolio. Therefore, the new asset will affect the risk of the portfolio through its contribution to the average covariance of the portfolio. Thus cov(ri, rp), or the covariance of the returns of the new asset with those of the existing portfolio measures the riskiness of a security when investors hold well diversified portfolios.
Next, from above we know that since all investors want to maximize the benefits of diversification, we can assume that they will all hold the market portfolio. Therefore, the riskiness of an individual asset i can be measured as cov(ri, rm).
8.10 The CAPM
Finally, we draw together all of the building blocks developed above into a final equation known as the Capital Asset Pricing Model. We begin by postulating that the expected return of any asset is given by a formula of the form:
E[ri] = rf + [Number of Units of Risk][Risk Premium per Unit]
We have established above that the appropriate measure of risk is cov(Ri, Rm) and hence, the equation can be rewritten as:
![]()
We already know the details surrounding two points on this line. The
riskless asset has expected return of rf and covariance with the market
portfolio of zero (since rf is constant). The market portfolio has expected
return E[rm] and covariance with the market of ![]() (the covariance of a variable with itself is its variance). Since these
two points must lie on the line, the equation to the line must be:
(the covariance of a variable with itself is its variance). Since these
two points must lie on the line, the equation to the line must be:
![]()
Note that for the riskless asset this becomes:
![]()
and for the market portfolio it is
![]()
It is common to standardize the units of this equation by defining ![]() and rewriting the equation as
and rewriting the equation as
![]()
It is this equation that is know as the Sharpe-Lintner CAPM. Note that the beta of the market portfolio is one:
![]()
This provides a reference point against which the risk of other assets can be measured. The average risk (or beta) of all assets is the beta of the market, which is one. Assets or portfolios that have a beta greater than one have above average risk, tending to move more than the market. For example, if the riskless rate of interest (T-bill rate) is 5% p.a. and the market rises by 10%, assets with a beta of 2 will tend to increase by 15%. If however, the market falls by 10%, assets with a beta of 2 will tend to fall by 25% on average. Conversely, assets with betas less than one are of below average risk and tend to move less than the market portfolio. Assets that have betas less than zero tend to move in the opposite direction to the market. These assets are known as hedge assets.
8.11 Security Market Line
The following figure shows the relationship between beta and expected return, which is known as the Security Market Line (SML).

The next figure contrasts the security market line with the capital market line, highlighting the difference between systematic risk (which is priced) and diversifiable risk (which is not priced).

Notice in the following figure that the systematic risk of IBM is measured by its covariance with the returns of the market. For each unit of market risk (standard deviation), IBM has cov[rIBM, rm] units of systematic risk, so that the systematic risk of IBM in the CML is
![]()
This can be obtained by using the properties of a straight line:
![]()
so that:
![]()
Using ![]() and
and ![]() yields the result.
yields the result.
The above derivation of the CAPM measure assumes that all individuals hold the same portfolio and that this portfolio must be the market portfolio. The most general version of the CAPM requires only that individuals hold mean variance efficient portfolios. In this version, each individual can hold a different portfolio of risky assets. The market portfolio, which is just a weighted sum of the individuals portfolios, will itself be on the efficient frontier and hence will be an efficient portfolio. This more general version of the CAPM also relaxes the assumption that individuals can borrow and lend at the riskless rate. In fact, it treats all assets as risky. Rather than relying on the existence of a riskless asset, all that is required is the existence of an asset whose returns are uncorrelated with those of the market portfolio (a zero-beta portfolio). The final equation for this model is:
![]()
where E[rz] is the expected return of the zero-beta portfolio and the other variables are as previously defined. This version of the CAPM is know as the Black CAPM and was derived by Fischer Black.
Click here for a mathematical derivation of CAPM (For interested students with advanced skills in mathematics).
8.13 Implementing the CAPM
In the previous section, we derived a relation between expected excess returns on an individual security and the beta of the security. We can write this as a regression equation. This is a special regression where the intercept is equal to zero.
![]()
This holds for all i. The beta is the covariance between the security i's return and the market return divided by the variance of the market return.
So the CAPM delivers an expected value for security i's excess return that is linear in the beta which is security specific. We will interpret the beta as the individual security's contribution to the variance of the entire portfolio. When we talk about the security's risk, we will be referring to its contribution to the variance of the portfolio's return -- not to the individual security's variance.
This relation holds for all securities and portfolios.
| Example 8.14
If we are given a portfolio's beta and the expected excess return on the market, we can calculate its expected return. Finally, we have a tool which we can help us evaluate the advertisement presented in the Diversification lecture. The ad that appeared in the Wall Street Journal provided data on Franklin Income Fund and some other popular portfolios. The returns over the past 15 years were:
First, let's convert these returns into average annual returns:
Note that the average annual returns are not nearly as impressive as the total return over 15 years. This is due to the compounding of the returns. In order to use the CAPM, we need some extra data. We need the expected return on the market portfolio, the security or portfolio betas and the riskfree rate. Suppose that the average return on the market portfolio is 13% and the riskfree return is 7%. Furthermore, suppose the betas of the portfolios are:
These are reasonable beta estimates. The Dow is composed of 30 blue chip securities that are generally less risky than the market. Remember that the beta of the market is 1.00. Any security that has a beta greater than 1.00 is said to have extra market risk (extra-market covariance). The long-term bond portfolio has a very low market risk. If we had a short-term bond portfolio, it would have even lower market risk (beta would probably be 0.10). I have made a conservative estimate that the beta of Franklin is equal to the beta of the market. In reality, The Franklin Growth Fund probably has a beta that is much higher because growth stocks are usually small and have higher market risk. Income stocks are usually larger and have market risk about equal to the market or lower. Now let's calculate the expected excess returns on each of these portfolios using the CAPM.
Note that the expected returns for the Dow and the Salomon Bond Index were exactly what the actual average returns were. Note also that the expected return on the Franklin Income Fund was higher than what was realized. The market expected 13% performance and the Fund delivered 12.9%. The difference between the expected performance and the actual is called the abnormal return. The abnormal return is often used in performance evaluation. So now we have a powerful tool with which to calculate expected returns for securities and portfolios. We can go beyond examination of historical returns and determine what the risk adjusted expected return for the security is. |
To get a deeper insight into risk, consider the estimation of the beta coefficient from an ordinary least squares regression:
![]()
In this regression, the beta is the ratio of the covariance to the variance of the market return. The alpha is the intercept in the regression. This is not the CAPM equation. This is a regression that allows us to estimate the stock's beta coefficient. The CAPM equation suggests that the higher the beta, the higher the expected return. Note that this is the only type of risk that is rewarded in the CAPM. The beta risk is referred to in some text books as systematic or non-diversifiable or market risk. This risk is rewarded with expected return. There is another type of risk which is called non-systematic or diversifiable, non-market or idiosyncratic risk. This type of risk is the residual term in the above time-series regression.

The asset's characteristic line is the line of the best fit for the scatter plot that represents simultaneous excess returns on the asset and on the market.

This is just the fitted values from a regression line. As mentioned above, the beta will be the regression slope and the alpha will be the intercept. The error in the regression, epsilon, is the distance from the line (predicted) to each point on the graph (actual).
The CAPM implies that the alpha is zero. So we can interpret, in the context of the CAPM, the alpha as the difference between the expected excess return on the security and the actual return. The alpha for Franklin would have been -.10 whereas the alpha for both the Dow and the Salomon Bonds were zero.
8.16 IBM's Alpha and Beta
Any security's alpha and beta can be estimated with an ordinary least squares regression. I have provided some results for IBM from 1926--1994. The returns data comes from the Center for Research in Security Prices (CRSP) and the riskfree return is the return on the one month Treasury Bill from Ibbotson Associates. This type of regression is usually estimated over 5 year sub-periods if the data is monthly. The market index used is the CRSP value weighted NYSE stock index. Value weighting means that stock i is given a weight equal to the market value of the stock of i divided by the market value of all securities on the NYSE.
Usually, this type of regression is estimated over 5 year sub-periods. I have provided estimates over the entire time period and some shorter subperiods. The results are summarized below.
|
Time |
Alpha |
T-Stat |
Beta |
T-Stat |
R2 |
|
1926-95 |
0.0076 |
4.3 |
0.79 |
25.5 |
0.48 |
|
1926-35 |
0.0148 |
2.8 |
0.79 |
14.4 |
0.64 |
|
1936-45 |
0.0058 |
1.6 |
0.49 |
8.4 |
0.37 |
|
1946-55 |
0.0080 |
1.9 |
0.83 |
7.5 |
0.33 |
|
1956-65 |
0.0091 |
2.2 |
1.39 |
11.6 |
0.53 |
|
1966-75 |
0.0040 |
0.9 |
0.89 |
10.2 |
0.47 |
|
1976-85 |
0.0017 |
0.4 |
0.82 |
9.1 |
0.41 |
|
1986-95 |
-0.0011 |
0.5 |
0.93 |
8.1 |
0.39 |
|
1971-75 |
-0.0019 |
-0.3 |
0.88 |
7.2 |
0.47 |
|
1976-80 |
-0.0043 |
-0.9 |
0.87 |
8.0 |
0.52 |
|
1981-85 |
0.0075 |
1.3 |
0.77 |
5.3 |
0.33 |
|
1986-90 |
0.0035 |
0.9 |
0.89 |
4.3 |
0.37 |
|
1991-95 |
-0.0045 |
0.8 |
0.97 |
6.3 |
0.43 |
The results indicate that the beta of IBM varied between .5 to 1.4 over the period examined. In recent years (from 1971), the beta has been around 0.9. Notice that in recent years that the alpha is indistinguishable from zero. This indicates that there has been no abnormal return from investing in IBM.
The beta of an individual asset is:

Now consider a portfolio with weights wp. The portfolio beta is:

The beta of the portfolio is the weighted average of the individual asset betas where the weights are the portfolio weights. So we can think of constructing a portfolio with whatever beta we want. All the information that we need is the betas of the underlying asset. For example, if I wanted to construct a portfolio with zero market (or systematic) risk, then I should choose an appropriate combination of securities and weights that delivers a portfolio beta of zero.
As an example of some portfolio betas, the next table includes some average beta values for industry portfolios. These betas are ranked by size. The industry with the highest beta was Air Transport and the lowest beta industry was Gold Mining.
| Industry |
Beta |
| Air transport |
1.80 |
| Real Property |
1.70 |
| Travel, outdoor rec. |
1.66 |
| Electronics |
1.60 |
| Misc. Finance |
1.60 |
| Nondurables, entertain |
1.47 |
| Consumer durables |
1.44 |
| Business machines |
1.43 |
| Retail, general |
1.43 |
| Media |
1.39 |
| Insurance |
1.34 |
| Trucking, freight |
1.31 |
| Producer goods |
1.30 |
| Aerospace |
1.30 |
| Business services |
1.28 |
| Apparel |
1.27 |
| Construction |
1.27 |
| Motor vehicles |
1.27 |
| Photographic, optical |
1.24 |
| Chemicals |
1.22 |
| Energy, raw materials |
1.22 |
| Tires, rubber goods |
1.21 |
| Railroads, shipping |
1.19 |
| Forest products, paper |
1.16 |
| Miscellaneous, conglom |
1.14 |
| Drugs Medicine |
1.14 |
| Domestic oil |
1.12 |
| Soaps, cosmetics |
1.09 |
| Steel |
1.02 |
| Containers |
1.01 |
| Nonferrous metals |
0.99 |
| Agriculture |
0.99 |
| Liquor |
0.89 |
| International oil |
0.85 |
| Banks |
0.81 |
| Tobacco |
0.80 |
| Telephone |
0.75 |
| Energy, utilities |
0.60 |
| Gold |
0.36 |
Recall that the net present value of a project (NPV) is
![]()
or
NPV = PV[Future Cash Flows] - Initial Investment Cost
where Delta(Xt) is the expected incremental net cash flow from the project in year t; n is the number of cash flows generated by the investment; I is the initial investment rp is the required return for this particular project.
In a world of uncertainty, rp, is the return required for the risk involved and is given by the CAPM. The CAPM states that the expected return on any risky asset equals the risk-free rate of interest plus a risk premium equal to the market risk premium times the assetís beta, that is,
Now, consider the marginal cost of capital for an all-equity firm (rproject). Assuming that the investment that the firm is considering is in the same risk class as the firm, the marginal cost of capital for the investment project can be computed by estimating the stockís beta, the market risk premium, and the riskless rate of interest, and substituting into the CAPM equation above.
| Example 8.19
Consider the following investment opportunity available to a firm.
This investment opportunity is in the same risk class as the other investments of the firm. The expected return on the market is 12%, the risk free rate is 8% and the firmís stock has a beta = 1.5. Should the firm undertake this investment (assume that the firm is all equity)? First, we acknowledge that this is a risky investment and calculate the required return for the risk involved. This required return is given by the CAPM as follows:
Thus the required rate of return, rp is 14%. Finally, we can calculate the NPV in the usual way using rp = 14%.
Since NPV>0 we accept this project. |
| Example 8.20
Assume now that the investment opportunity available to the firm is in a different industry to that of the firmís normal operations. This industry is 40% riskier than the firmís industry. If the cash flows are as above and the expected return on the market is 12%, the riskfree rate is 8% and the firmís beta = 1.5, should the firm undertake the investment? Again, we recognize the fact that the firm is confronted by a risky investment and calculate the return required for the risk involved. Since this investment is 40% riskier than the normal investments of the firm, the beta of the investment is given by beta = 1.4(1.5) = 2.1. Hence, the required return is given by:
Thus the required rate of return, rp, is 16.4%. Again, we calculate the NPV in the usual way using rp = 16.4%.
Since NPV<0, we reject this proposal. |
| Example 8.21
The Marlet Fishing Boat Company currently has a market value of $4 million. Its required rate of return is 18%. The company is evaluating an $88,000 investment project which is expected to generate after-tax cash flows of $176,000 a year indefinitely. The project is 40% riskier than the firmís average operations. If the riskless rate of interest is 8% should the project be accepted? Assume that the market risk premium (E[rm] - rf ) = 7.5%. First, we calculate the required return for the risk involved. We are not told the beta of the normal investments, but we do know that:
for a normal project. Since this project is 40% riskier, we know that
So the beta of the project is 1.8666 Plugging this back into the CAPM yields:
Hence, the required rate of return, rp = 22% and the NPV is given by NPV = ($176,000 / 0.22) - $800,000 = 0 Hence we are indifferent between undertaking the project or rejecting it. |
8.22 Tests of the CAPM
Let's review what we have learned so far. There is a statistical model that describes realized excess returns through time:
![]()
This type of model can be estimated with ordinary least squares regression. We assume that the expected value of the error is zero and that it is uncorrelated with the independent variable. We also took expected values of each side of this model:
![]()
which looks like the CAPM. But the asset pricing model that we developed imposes the following constraint on expected returns:

for all securities i.
The security's expected excess return is linear in the security's beta. The beta represents the risk of security i in the market portfolio -- or the contribution of security i to the variance of the market portfolio. The beta risk is the only type of risk that is rewarded or priced in equilibrium. What makes the CAPM different from the statistical model is that the CAPM imposes the constraint that the intercept or alpha is zero.
We can also write the alpha in terms of actual and predicted returns. Security i has an excess return of:
![]()
The CAPM predicted excess return is:
![]()
So the alpha is:

Thus, the alpha measure risk adjusted performance of a security.
One test of the CAPM is to test whether the alpha of any security or portfolio is statistically different from zero. The regression would be run with available stock returns data. The null hypothesis is (the CAPM holds) is that the intercept is equal to zero. Under the alternative hypothesis, the intercept or alpha is not equal to zero. The standard test is a t-test on the intercept of the regression. If the intercept is more than 2 standard errors from zero (or having a t-statistic greater than 2), then there is evidence against the null hypothesis (the CAPM).
We have already seen the alpha coefficients for the IBM regression. Now consider Erb, Harvey and Viskanta "Expected Returns and Volatility in 135 Countries" In this paper, the authors regress country index returns on the Morgan Stanley World Market Portfolio. This is a world version of the Sharpe (1964) CAPM (Click here for the table). There are, however, potential problems with these tests.
8.24 Cross-Sectional Tests of the CAPM
The Capital Asset Pricing Model implies that each security's expected return is linear in its beta. A possible strategy for testing the model is to collect securities' betas at a particular point in time and to see if these betas can explain the cross-sectional differences in average returns. Consider the cross-sectional regression:
![]()
In this regression, R represents the returns of many securities at a particular cross-section of time and beta represents the betas on many firms.
According to the CAPM, ![]() should
be equal to zero and
should
be equal to zero and ![]() should equal
the expected excess return on the market portfolio. We can test this.
should equal
the expected excess return on the market portfolio. We can test this.
The first tests of the theory were carried out by Black, Jensen and Scholes (1972) and Fama and MacBeth (1973). Both of these tests were cross sectional tests. We will examine the Black, Jensen and Scholes (1972). Portfolios of stocks are created ranging from high beta portfolios to low beta portfolios. A cross sectional regression was run to see if the betas were able to explain the differences in the returns across securities.
![]()
The results are:

The t-statistics are in parentheses.
The CAPM theory suggests that ![]() = 0. The regression evidence provides evidence against that hypothesis.
The CAPM theory also suggests that
= 0. The regression evidence provides evidence against that hypothesis.
The CAPM theory also suggests that ![]() >0 and is equal to the expected return on the market less the risk free
rate. Over the period 1931--1965, the average return on the market less
the risk free rate was 0.0142. The regression evidence suggested a coefficient
of 0.0108. The evidence suggests that there is a positive trade off between
risk and return -- but the
>0 and is equal to the expected return on the market less the risk free
rate. Over the period 1931--1965, the average return on the market less
the risk free rate was 0.0142. The regression evidence suggested a coefficient
of 0.0108. The evidence suggests that there is a positive trade off between
risk and return -- but the ![]() coefficient
is lower than expected.
coefficient
is lower than expected.
As reviewed previously, there are many possible explanations as to why the data does not exactly support the CAPM. However, the CAPM is a benchmark that is often used in risk analysis.
8.25 Conditional Asset Pricing
We have examined the following pricing relation
![]()
Where:

The pricing model implies that the market portfolio is mean-variance efficient. Note that the pricing relation is written in terms of unconditional expected returns and risk. That is, average risk is related to average expected returns.
The tests of the model that we have studied have worried about the assumption that the risk is constant through time. For example, in the tests of Fama and MacBeth, the betas were estimated over a five year period. Five years is the conventional window. It is thought that anything longer might be problematic -- because the beta may change.
The expected returns could also be changing through time. If expected returns were constant, and if we regressed an asset return at time t on a constant and a number of information variables available at time t-1, then only the intercept should be significantly different from zero. The fitted values in this regression (the expected returns) would then be a constant (the value of the intercept). However, if the information variables enter the regression with coefficients that are significantly different from zero, then the fitted values from the regression will not be constant. This implies that the expected returns are changing through time. We explore possibilities of allowing the risk and expected returns to change through time.
It is possible to write the asset pricing relation at the conditional level:

where the lower case r denotes returns in excess of a risk free return and Z denotes the information variables available to investors. The CAPM restricts the conditionally expected returns to be linearly related to conditionally expected excess returns on a market wide portfolio. The coefficient in the linear relation is the asset's beta or the ratio of the conditional covariance with the market to the conditional variance of the market.
We know that the expected returns on the asset change through time. It is likely that the conditional covariance of the asset and the market also changes through time (firm may change its business risk by investing in new projects).
Harvey "Time-Varying Conditional Covariances in Tests of Asset Pricing Models" (P3) and "The World Price of Covariance Risk" (P10) develops methodologies to implement asset pricing tests with time-varying covariances, variances and expected market premiums.
Ferson and Harvey "The Variation of Economic Risk Premiums" (P5) show that most of the predictability in portfolio returns is due to time-varying risk premiums (as opposed to the covariances and variances). These studies provide the foundation for the Global Tactical Asset Allocation course.
Tests of this formulation of the model are tests of whether the 'market' portfolio is conditionally mean-variance efficient. Think of the efficient frontier being drawn at every point in time. The model implies that the market portfolio is the tangency portfolio on every frontier through time.
The methodology presented for conditional asset pricing can easily be applied to tactical asset allocation strategies. At the conditional level, one needs conditionally expected returns, conditional covariances and conditional variances as inputs into the allocation program. The above approach can be used to do this.
8.27 Multirisk formulations
The goal of most economic models is to simplify reality so that we can gain a greater understanding of how the world works. The CAPM is an example of a simplification. A very complicated process (how prices are set in equilibrium) is reduced to a single firm-specific parameter -- the beta. The beta is multiplied by the risk premium for beta (the expected excess return on the market portfolio) to obtain the expected excess return on the security.
Obviously, the CAPM is a very simple model. As for all models, with enough data we can ``statistically" reject the model. However, this does not mean that the model is not useful. On the contrary, a rejection of the model leads us to refinement and expansion of the generality of the model. One of the most obvious sources of generalization is to add additional risk factors.
Assetpricing theory has been generalized to multiple sources of risk in important papers by Ross (1976, Journal of Economic Theory), Sharpe (1982), Merton (1973, Econometrica) and Long (Journal of Financial Economics, 1974).
The intuition of these models is that assets have exposures to various types of risk: inflation risk, business-cycle risk, interest rate risk, exchange rate risk, and default risk. It is difficult to capture all of these risk measures with the beta of the CAPM. The multirisk models have multiple betas. Instead of running a regression of the asset return at time t on the market return at time t, we run a regression of the asset return at time t on various "factors" at time t, like the change in the interest rate. The betas from this augmented regression are sometimes called factor loadings, risk sensitivities or risk exposures. The basic idea of the CAPM is maintained. The higher the exposure the greater the expected return on the asset.
Multifactor asset pricing formulations which tried to explain average returns with average risk loadings in Roll and Ross (1980, Journal of Finance) and Chen, Roll and Ross (1986, Journal of Business). However, these studies assume that risk is constant, risk premiums are constant and expected returns are constant.
Ferson and Harvey "The Variation of Economic Risk Premiums" (P5) examines a model which uses multiple factors but lets all the parameters of the model shift through time. Ferson and Harvey "The Risk and Predictability of International Asset Returns" (P21) extends the dynamic factor model to an international setting. Harvey "Predictable Risk and Returns in Emerging Markets" (P32) explores a similar formulation in emerging capital markets.
Another popular formulation is the 3-factor model of Fama and French (1993). In this model, there are three betas. The stock returns are regressed on (1) the market; (2) a High book value to market value portfolio Minus Low book value to market value portfolio (HML); and (3) a Small capitalization portfolio Minus a Big capitalization portfolio (SMB). The first beta is the standard beta from the CAPM. The second beta measures distress (high book to market ratios are indictative of firms in distress). The third beta captures the size of the firm which is often correlated with risk.
While the Fama and French (1993) work has received much attention, Ferson and Harvey ``Conditioning Variables and the Cross-Section of Stock Returns," (W32) argue that the model has some substantial short-comings. Ferson and Harvey argue that (1) the risk functions need to change through time (i.e. the betas are changing through time) and (2) the model misses an important factor related to interest rates.
While substantial advances have been made in asset pricing theory, there is still much work to be done. In addition, standard asset pricing models need to be modified to be applied to international settings. For example, Bekaert and Harvey (1995) ``Time-Varying World Market Integration,'' Journal of Finance(P33) detail the impact of capital market integration on asset pricing. Two markets are integrated when the same risk project commands the same expected returns in both markets. Regulations that prevent foreigners from transacting in the domestic market or that prevent domestic investors from diversifying their portfolios internationally lead to market segmentation.
Acknowledgement
Some of the material for this lecture is drawn from Douglas Breeden, "Capital Asset Pricing Model: Tests and Extensions".