![]()
Copyright 1997 by Campbell R. Harvey and Stephen Gray. All rights reserved. No part of this lecture may be reproduced without the permission of the authors.
Latest Revision: February 27, 1997
7.0 Overview
This class provides an overview of individual asset allocation. It is shown that an individual can reduce the risk of his portfolio without sacrificing any expected return simply by spreading his wealth over a number of assets in an appropriate way. This technique of diversification is explained in some detail in terms of a simple two-asset example in order to build intuition.
7.1 Objectives
After completing this class, you should be able to:
7.2 Introduction
So far in the course, we have not established any benchmarks to compare securities or portfolios other than expected returns. It is impossible to judge the quality of an investment be simply looking at its expected returns. For example, consider an advertisement from The Wall Street Journal which followed the following performance comparison.
|
The Franklin |
Dow Jones |
Salomon's High |
Cost of Living |
|
516% |
384% |
283% |
169% |
These average returns over the past 15 years are higher than the Dow Jones Industrial Average and Salomon's High Grade Bonds. Does this mean that we can beat the market by investing in Franklin now? The answer is no. The advertisement tells us nothing about the risk of the Franklin Fund. We will always want to consider risk as well as return. The Franklin Fund stocks may be very risky and the only way people will hold the component stocks is to have a high expected return. So we have go beyond returns and develop a model of risk that allows us to compare stocks and portfolios.
There are many models of risk and expected return. Two popular models are: the Capital Asset Pricing Model (CAPM) and the Arbitrage Pricing Theory (APT). We will spend most of our time examining the Capital Asset Pricing Model. The CAPM was the first of the pricing models [William Sharpe (1964)] and the most commonly used by practitioners.
The APT or multifactor CAPM (Stephen Ross) is examined in considerable detail in the elective courses. I will briefly introduce these models after we have finished with the CAPM.
7.3 The Planning Problem
The Capital Asset Pricing Model is an equilibrium model. The prices that exist in the economy are a result of all consumers maximizing utility and markets clearing, i.e., prices are set such that supply equals demand. Our goal is to create (model) a simple economy with these ingredients and see if the pricing function has power to predict actual prices in the economy. A simple economy involves simple assumptions. After we derive the CAPM, you will note that many assumptions have been made that are not very realistic. But caution should be taken in judging a model by its assumptions. It is often better to judge a model by its ability to predict.
The consumers in our model are rational utility maximizers. The objective
of each person is to maximize expected utility of consumption today, plus
the expected utility of wealth, E[U(W)],
(future consumption) tomorrow. Mathematically, the consumer chooses c0
consumption today. Importantly, wi are the portfolio
weights for the N assets we could invest in today.
We will also assume that
U' > 0 and U" < 0
These are conditions on the form of the utility function. The first derivative being greater than zero means that you prefer more wealth to less wealth. This is a property that is not controversial. The second derivative being negative means that you prefer more to less at a decreasing rate as wealth gets larger. So you get more utility from a $10,000 increase in your wealth if your previous wealth was $20,000 rather than $2,000,000.
The variables to be maximized are the control variables. The consumer will be choosing: consumption today, c0, and investment proportions in N assets, wi. We will assume that one of these assets, i = 0, is risk free. So the consumer will use his initial wealth for either consumption today or investment in assets that pay off in the future. A constraint is necessary:
![]()
This just says that the sum of today's consumption plus investment in the N assets with price Pi, cannot exceed initial wealth. This is often referred to as the budget constraint. Tomorrow's wealth will be determined by the payoffs on the investment strategy. Because these payoffs or returns are random (except for the risk free asset), tomorrow's wealth will also be random.
7.4 Risk Aversion
One of the foundational principles of microeconomics is that economic agents can be modeled as risk averse utility maximizers. In Finance, we continue to employ this principle in determining how investors will evaluate risky investment proposals. In particular we employ two key assumptions:
A standard utility function that exhibits these two traits is illustrated in Figure 1.

Figure 1
The fact that the utility function is upward sloping indicates that the investor prefers more to less, no matter how wealthy he might become. The fact that the utility function is concave indicates that the investor is risk averse, a principle that is illustrated further below.
The following table llustrates in more detail how a risk-averse investor who prefers more to less may evaluate an investment proposal. In particular, we can define an individual to be risk averse if he chooses not to undertake an investment that provides a 50/50 chance of an increase or decrease in wealth of $x. For example, suppose that an investor is faced with a gamble whereby he bets $100 on the toss of a coin. If it's heads he wins $200, if it's tails he gets nothing. This gamble creates a 50/50 chance of increasing or decreasing his wealth by $100, so his expected wealth is unchanged. However, if the investor is risk averse, he will actually pay to avoid being subjected to this risk.
The bet can be summarized as:
|
Outcome |
Probability |
|
$x |
50% |
|
-$x |
50% |
The investor would be pleased if the outcome turns out to be x, which is illustrated by the increase in utility on the graph U. However, the investor would be extremely displeased if the outcome turns out to be -x. The decrease in his utility D when the outcome is -x is far greater than the increase in his utility when the outcome is +x. This discussion illustrates that in general a risk averse individual will never take a fair bet.
| Example 7.5
Suppose that an investor with initial wealth W0 = 20.5 has the utility function
and is faced with the following investment proposal:
The investor's current utility is (20.5)0.5 = 4.53. If the investment succeeds, the outcome is +4.5 and the increase in the investor's utility is D = 4.53 - (20.5-4.5)0.5 = (4.53-4) = 0.53. Since each outcome occurs with 50% probability, the expected utility of the investor after undertaking the investment is:
However, the investor currently has utility of U(W0) = U(20.5) = 4.53. Hence, he is worse off if he undertakes the investment and therefore will not accept it. This is illustrated in the figure below. This example illustrates the expected utility rule: If the expected utility E[U(W)] from owning a proposed investment exceeds the current utility U(W0) without the investment, then the investment should be undertaken. That is, if E[U(W)] > U(W0) then the investor will undertake the investment.
|
| Example 7.6
What if the gamble is not fair, so that the odds are stacked in the investor's favor (i.e., xu > xd)? Whether an individual takes the gamble or not depends on his utility function, and on his initial wealth. First, suppose the individual has utility, U(W) = W0.5, initial wealth of 20, and is faced with the following investment proposal:
In this case, the investment proposal is better than a fair bet and whether an individual takes it depends on his utility function. What is the expected utility after undertaking the investment?
His current utility (without the investment) is: U(W0) = U(20) = (20)0.5 = 4.47 Therefore, since E[U(W)] > U(W0), the investor should accept the investment proposal.
|
| Example 7.7
Now suppose that the individual's utility function is logarithmic so that U(W) = ln W. What is the expected utility after undertaking the investment?
His current utility (without the investment) is: U(W0) = U(20) = ln(20) = 3.00 Therefore, since E[U(W)] < U(W0), the investor should not accept the investment proposal. Finally, suppose that the investor still has log utility, but that his initial wealth is 100 (rather than 20). In this case, the expected utility after undertaking the investment is:
The investor's current utility (without the investment) is U(W0) = ln(100) = 4.60. Therefore, since E[U(W)] > U(W0), the investor should accept the investment proposal. |
This example indicates that different investors have different attitudes toward risk, which is captured in the form of differently shaped utility functions. Moreover, a single individual, whose utility function does not change can become more tolerant toward risk as his wealth increases.
7.8 Certainty Equivalent
The certainty equivalent C is the minimum amount of cash that an investor would accept in exchange for all of his investments and his initial wealth. Having $C cash will make the investor as well off as having his initial wealth and his investment portfolio. Therefore:
E[U(W)] = U(C)
| Example 7.9
Suppose an investor, who has square root utility and initial wealth of $100,000, is deciding whether or not to buy car insurance. The outcomes and associated probabilities, based on the investor's driving record are:
First, determine the investor's expected utility if he does not buy insurance:
Next, compute the certainty equivalent so that the investor is just as happy with $C cash as with having $100,000 and taking the risk of the accident. That is, $C solves:
The investor originally had $100,000 (W0) plus the risk of an accident. If he had $97,092.07 and was indemnified against the cost of an accident, he would be just as happy. Therefore, he is prepared to pay $100,000 - 97,092.07 = $2,907.93 for car insurance. |
General forms of risk averse, risk neutral and risk loving preference functions are shown below:

Figure 4

Figure 5

figure 6
Click here for a supplementary discussion on the Cost of Risk
Portfolios of assets can be compared on the basis of their risk and return characteristics. In this section we consider tools for analyzing portfolios. We need to know how to measure the risk and return characteristics of a given portfolio of securities.
7.11 Two Asset Case
The expected return of a two asset portfolio is simply a weighted average of the expected returns of each asset in the portfolio.
E[rp] = w1 E[r1] + (1-w1) E[r2] (Eq 1)
where w1 and (1-w1) = w2 are the percentage of portfolio value invested in each asset.
From basic statistics we also know that the variance of two random variables is a function of the variance of each variable and the covariance between the variables. This relationship directly applies in calculating the variance of a two asset portfolio as follows:
![]() (Eq
2)
(Eq
2)
7.12 The N Asset Case
For an N asset portfolio, the portfolio return is just the sum of the asset returns times the weights each of the assets has in the portfolio. In matrix notation, this is just the product:
rp = w' r (Eq 3)
w is a vector containing the respective weights of the N assets. That is, if we have $1 million to invest and we place $100,000 in security i, then wi = 0.10. We define r as a vector containing the returns of the N assets. This product can be calculated in Excel using the sumproduct function.
The weights must all sum to one. This means that all money must be allocated.
The portfolio expected return is just the expected asset returns times the weights each of the assets has in the portfolio.
The portfolio expected return is just the sum of the expected asset returns times the weights each of the assets has in the portfolio. If E is a vector containing the expected returns of the assets, then the portfolio's expected return can also be defined in terms of matrix multiplication. In Excel this operation can also be performed using the sumproduct function.
Ep = w' E
Note that the above formula expands to the formula above for the two asset case.
E(rp) = w1 E(r1) + (1-w1) E(r2)
The portfolio expected excess return is just the expected returns on the assets minus the risk free return (say a one month Treasury bill) times the weights each of the assets has in the portfolio. This value can also be expressed as a product of a (1 x N) matrix of weights with a (N x 1) matrix of excess returns (or in Excel using the sumproduct function).
Xp = w'X
where X represents the expected excess returns on the various assets.
The variance of the portfolio return is a little more complicated when there are more than two assets. It will still be a function of the weights, variances and covariances, but it is harder to express as a simple formula. It can be expressed, easily, as a product of matrices:
![]() (Eq
5)
(Eq
5)
where V is the variance-covariance matrix (variances along diagonal and covariances off the diagonal). The linear algebra is shown below for the two asset case.

The matrix algebra for the N asset case can easily be implemented in Excel.
The covariance of two portfolio returns, each denoted by their own set of weights, say wa, wb can also be found using matrix algebra. It is just:
Cova,b = wa' V wb (Eq 6)
where V is the variance-covariance matrix (variances along diagonal and covariances off the diagonal).
Recall the formula for correlation. The correlation of portfolios with returns a and b is just the covariance divided by the product of the standard deviations.
Given an optimal choice for today's consumption, c0, the goal of a portfolio is to maximize the utility (expected) of future consumption provided by wealth at t = 1. This is a hard problem.
Often we need to make a major assumption to simplify the problem. We will assume that asset returns are jointly normally distributed. The normal distribution has the property that the distribution can be completely described by two parameters: the mean and variance. The multivariate normal can be completely described by the means, variances and the covariances between the different assets.
Note the variances and the covariances of the risk free asset are zero.
A linear combination of normal random variables is normal. Therefore, wealth at t = 1 is normally distributed. The entire probability distribution of wealth is described by a portfolio's mean and variance. This all implies that a sufficient set of statistics to discriminate between portfolios is the mean and variance. This greatly simplifies the portfolio selection problem.
7.14 Other Distributional Assumptions
While most of finance is set in a mean-variance framework (which lends itself to using the normal distribution), there is some new work going on which tries to capture more general distributions. Harvey and Siddique (1995) have cast the portfolio selection in terms of mean-variance-skewness. This idea originates with important work in the 1970s. Harvey and Siddique make the means, variances and skewness dynamic processes which change with economic conditions. This paper is discussed in Global Tactical Asset Allocation.
7.15 The Effect of Diversification
Now let's consider the effect of diversification. We will examine a portfolio of two assets. From our formula for variance, we know:
![]()
Where ![]() is the portfolio
variance. For the two asset case:
is the portfolio
variance. For the two asset case:
![]()
where ![]() is the covariance
between assets 1 and 2.
is the covariance
between assets 1 and 2.
We could also write this in terms of correlation:
![]() (Eq
7)
(Eq
7)
where the sigmas denotes the standard deviation of assets 1 and 2.
For simplicity, assume in the following examples, that the variances
of the two assets are equal, or ![]() and
that the portfolio weights are identical, or w1 = w2
= 0.50.
and
that the portfolio weights are identical, or w1 = w2
= 0.50.
| Example 7.16 Perfect
Positive Correlation The first case of interest is that of perfect positive correlation. Using the formula:
This result demonstrates that the portfolio variance is the same as the variance for each asset. So diversification does not reduce the portfolio variance in this case. |
| Example 7.17 No Correlation
The second case of interest is that of zero correlation. Again, plugging into the formula:
This result demonstrates that the portfolio variance is half of the variance of the individual assets. So combining stocks that have less than perfect positive correlation is a strategy that will reduce the variance of the returns on your portfolio. This is called diversification. |
| Example 7.18 Perfect Negative Correlation
If two assets could be found which have perfect negative correlation, then we combine these assets to create a risk free portfolio:
These assets create a perfect hedge. This shows that diversification can be thought of as a partial hedge of risks. |
The following graphs tells the story. Suppose we randomly selected a stock and plotted its standard deviation. Now we randomly draw another stock and plot the standard deviation of the equally weighted portfolio. We continue the exercise. Just by randomly selecting stocks we can decrease portfolio variance.

figure 7
| Example 7.19
Suppose Assets 1 and 2 have expected returns and standard deviations as follows:
Furthermore, suppose that the returns of the two securities are perfectly
negatively correlated with Here we use equation 1 to compute the expected return of the portfolio: E[rp] = w1 E[r1]+(1-w1)E[r2] and since the weight of each asset is w1 = w2 = 0.5, we find that E[rp] = 0.5 (20%) + 0.5 (10%) = 15% We use equation 7 to compute the variance of the returns of the portfolio:
Plugging in the values for our 50/50 portfolio yields (0.52)(0.202) + (0.52)(0.162) + 2 (0.5)(0.5)(0.20)(0.16)(-1) = 0.0004 in which case the standard deviation of the returns of the portfolio is 0.02 = 2%. Recall that Asset 2 has an expected return of 10% and a standard deviation of 16%. Clearly this portfolio of equal weights in Asset 1 and Asset 2 is preferred to holding Asset 2 by itself since the portfolio has an expected return of 15% and a standard deviation of 2%. |
| Example 7.20
Consider forming a portfolio with three assets. The expected returns are E' = (0.25, 0.19, 0.12) The variance-covariance matrix is V
Portfolio 1 weights are w' = (.3, .4, .3) Portfolio 2 weights are w' = (.1, .6, .3)
Recall that the diagonal elements of the Variance/Covariance matrix contains the variances. The standard deviations can be found by taking the square roots of those variances. (0.090)0.5 = 0.300
The correlation coefficient can be calculated using the following relationship:
The covariances can be found in the V matrix where the covariances between assets j and k will be in row j, column k (and also in column j, row k).
Solving for the correlation coefficients:
Solving for the portfolio variances is easy, if you know how to multiply matrices using the following formula:
While matrix multiplication is not difficult, it is also not required for this class. The two asset case can be solved without matrix multiplication using the following formula:
Matrix multiplication can be performed in Excel using the mmult command. A sample spreadsheet can be downloaded, and modified to solve this problem. The solution for the first portfolio is:
The solution for the second portfolio is:
We can use equation 7
to find the covariance between these two portfolios. We could treat each of these portfolios as a separate asset, and create a new portfolio using equal weights. The variance of the new portfolio can be found, because it is just a portfolio of our three original assets. The varainces of the two portfolios can be plugged in to the right hand side of the equation. That leaves the covariance between the two portfolios as the only unknown. Solving for that, we find that the covariance between the two portfolios is 0.029040
|
7.21 Efficient Portfolios
Previously, we made the simplifying assumption that asset returns are multivariate normally distributed. This assumption implies that individual asset returns are univariate normally distributed. We make the assumption of normality because it greatly simplifies the portfolio selection problem. The entire distribution of an individual stock's return can be described by two parameters: the mean and the variance. We can figure out a portfolio's mean and variance by examining the means, variances and covariances of the component securities. Most importantly, we can compare different portfolios on the basis of mean and variance.
Our discussion of utility functions and risk aversion provided two conclusions. First, consumers like more to less. In terms of a security or portfolio, consumers prefer more return to less return. Second, consumers prefer less variance to more variance. Remember that the risk averse consumer will always turn down a fair bet. In terms of a security or portfolio, the consumer will prefer a portfolio with less variance to another higher variance portfolio with an equal expected return.
These insights lead to two rules of portfolio selection.
A portfolio that satisfies these conditions is known as an efficient portfolio. A portfolio is inefficient if there exists another portfolio with:

7.22 The Efficient Frontier
Build a two asset efficient frontier using a Java program.
Build a multiasset efficient frontier using a Java program.
We will now consider an example of the effects of diversification. Previously, we combined securities and looked at the effect on the portfolio variance for different correlation coefficients between the securities. We found that using equal weights in the two portfolios, a lower correlation coefficient led to lower portfolio variance. In this example, we will look at a given correlation and vary the portfolio weights to trace the effect on the portfolio variance.
The example comes from a classic article by Bodie and Rosansky, "Risk and Return in Commodity Futures" which was published in the Financial Analysts Journal in 1980. We will trace out the return and standard deviation of a portfolio of common stocks and futures. A number of tables are presented.
| Example 7.23
We will be concerned with the common stocks and the commodity futures. Note that the common stocks have a -24% correlation with the commodity futures. Previously, we showed that combining two portfolios with a zero correlation reduced the variance of the portfolio. This was referred to as diversification. The common stocks and futures have negative correlation. This suggests that holding both in a portfolio will produce a portfolio variance that is less than the variance of the individual components. Let's calculate the portfolio means and standard deviations. The two formulas that are relevant are: E[rp] = w1 E[r1] + (1-w1) E[r2] and
We are given that for Asset 1, the common stocks:
Also, Asset 2, the commodity futures:
We are also given the correlation coefficient and the variances can easily be calculated:
The next step is to calculate the portfolio mean and standard deviation for various weights.
Portfolio 1 (w1 = 1 w2 = 0) The mean return is: E[rp1] = 1 (13.05) + 0 (13.83) = 13.05% The standard deviation is:
Portfolio 2 (w1 = 0.8 w2 = 0.2) The mean return is: E[rp2] = 0.8 (13.05) + 0.2 (13.83) = 13.21% The standard deviation is:
Portfolio 3 (w1 = 0.6 w2 = 0.4) The mean return is: E[rp3] = 0.6 (13.05) + 0.4 (13.83) = 13.36% The standard deviation is:
Portfolio 4 (w1 = 0.4 w2 = 0.6) The mean return is: E[rp4] = 0.4 (13.05) + 0.6 (13.83) = 13.52% The standard deviation is:
Portfolio 5 (w1 = 0.2 w2 = 0.8) The mean return is: E[rp5] = 0.2 (13.05) + 0.8 (13.83) = 13.67% The standard deviation is:
Portfolio 6 (w1 = 0 w2 = 1) The mean return is: E[rp3] = 0 (13.05) + 1 (13.83) = 13.83% The standard deviation is:
These calculations verify the numbers presented in Table 5. The following graph shows the risk and return.
Note that with the negative correlation between the assets, the amount invested in the component securities has a large effect on the portfolio variance. |
7.24 The Efficient Frontier with Different Levels of Correlation
The next item is to look at the effect of different levels of correlations on the portfolio variance. Let's develop a better grasp of where these portfolios should lie in the mean-standard deviation space. In order to do this, assume that there are only two securities, q (1) and s (2). The expected return on the portfolio is:
E[rp] = w1 E[r1] + (1-w1) E[r2]
The standard deviation on the portfolio is:
![]()
Write this in terms of the correlation coefficient.
![]()
So now we can start to map out the frontier.
7.25 Perfect Positive Correlation
![]()
Consider a number of simple cases. First, if the correlation between the two securities is one, then the standard deviation on the portfolio is:
![]() (Eq
8)
(Eq
8)
because

This result has a simple geometric interpretation. If we plot the mean and standard deviation of the two securities, then a straight line between the two securities represents the set of portfolios available. The point q below represents the situation where w = 1 where as the point s represents the situation where w = 0. Note that diversification when the correlation between the securities is one is ineffective.

Figure 9: portfolio options (correlation = 1)
7.26 Perfect Negative Correlation ![]()
The second straightforward situation is when the correlation between the two securities is negative one. The standard deviation of the portfolio is:
![]() (Eq
9)
(Eq
9)
This immediately implies that we can drive the standard deviation of the portfolio to zero by choosing the right weights. Setting the left-hand side equal to zero, we can solve for w:
![]()
This point corresponds to the point y on the diagram. The expected return of this portfolio will be:


Figure 10: portfolio options (correlation = -1)
7.27 Correlation between -1 and +1
Finally, consider the case where the returns of the two assets are neither perfectly positively nor perfectly negatively correlated. Without loss of generality, assume that Asset 2 has lower variance than Asset 1, as depicted in Figures 11 and 12. In this case, two results are possible. If
![]()
there exists some portfolio of Assets 1 and 2 that has higher expected return and lower variance than Asset 2. That is, in this case there are gains from diversification. The possible portfolios lie on a parabola that has a turning point between Assets 1 and 2, as depicted in Figure 11.

Figure 11: Portfolio options with benefits from diversification
Alternatively, if
![]()
there does not exist any portfolio of Assets 1 and 2 that has higher expected return and lower variance than Asset 2. That is, in this case there are no gains from diversification.
The possible portfolios lie on a parabola that has no turning point between Assets 1 and 2, as depicted in Figure 12.
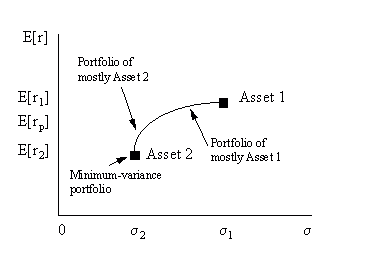
Figure 12: Portfolio options without benefits from diversification
| 7.28 Proof of claims
To prove these claims, we find the minimum variance portfolio and show that where
the minimum variance portfolio has lower variance and higher expected return than Asset 2. The minimum variance portfolio is found by solving:
which has the first order condition
Now the portfolio will have less risk than Asset 2 alone whenever : which was to be shown. |
Now let's consider the weights w. There is no restriction on the sign of w. Therefore, a negative w can be considered a short sale of security q. The dotted line extension of the lines in figure 13 represent short sales. Note that you can change the perfect positive correlation into negative correlation with the short sale provision.

Figure 13
More realistically, the correlation between the securities will between positive one and negative one. The curve on the diagram plots the possible portfolios with a correlation between zero and one.
Notice that any part of the curve that has a positive slope must be concave. Consider the counter example between u and v on the diagram. With a dashed line, I have drawn a convex segment. Is this a possible frontier? It turns out that the answer is no. We can consider u and v as separate portfolios of q and s. We know that the most extreme situation (farthest to the right) would be a correlation of positive one between these two portfolios. Hence, it is impossible to have any curve to the right of the straight line extreme case. So the frontier will be concave for all positive slopes.
Now letís be more precise. We have defined the mean-variance frontier. After plotting all the portfolio combinations, the points farthest the left are minimum variance. But consumers will only care about a certain portion of the frontier -- the portion with a positive slope. The negatively sloped part of the frontier implies a lower return for greater standard deviation. Our investors will not buy that trade-off. The positively sloped portion is called the efficient frontier. Portfolios on this frontier are referred to as mean--variance efficient. These portfolios maximize the expected return on the portfolio for a given variance. So there are dual properties of efficient portfolios:
No other portfolio with the same expected return has a lower standard deviation of return.
No other portfolio with the same standard deviation of return has a higher expected return
These properties are reflected in all the portfolios in the efficient frontier. The opportunity set for investors follows. Because of our assumptions about investors, only the positively sloping portion of the minimum variance curve is held. The solid line represents the efficient frontier. Note that I have also included arrows representing the direction of the investors' preferences (more return and less risk).

Figure 14

Figure 15
| Example 7.29
Suppose Assets 1 and 2 have expected returns and standard deviations as follows:
Also assume that the returns of the two securities are perfectly negatively
correlated Here we use the result that if
then the portfolio variance is zero. In this case, w1 = (16)/(20+16) = 0.44 which implies that 56% of the funds invested in the portfolio should be invested in Asset 2. The expected return of this portfolio is given by equation 1 E[rp] = (0.44) 20 + (0.56) 10 = 14.44% To check that the portfolio variance is indeed zero we use equation 7
|
| Example 7.30
Suppose that the correlation between the returns of the two assets from
the previous example is What is the minimum variance portfolio that can be formed from assets 1 and 2 and what is the expected return and standard deviation of the 50/50 portfolio? Finding the minimum variance portfolio is straightforward -- since the two assets are perfectly positively correlated, there are no gains from diversification and the minimum variance portfolio will be the portfolio that puts all the weight on Asset 2 (which has the lower variance) and zero weight on Asset 1. This portfolio amounts to holding Asset 2 by itself and yields an expected return of 10% and has a standard deviation of 16%. A portfolio of equal weights of Asset 1 and Asset 2 has expected return of E[rp] = (0.5) 20 + (0.5) 10 = 15% The variance of this portfolio is given by (0.5)2(20)2 + (0.5)2(16)2 + 2 (0.5)(0.5)(1)(20)(16) = 324 so the standard deviation is 18%. |
| Example 7.31
Suppose that the correlation between the returns of the two assets from
the previous example is What is the expected return and standard deviation of a portfolio with equal weights in each security? And what is the composition of the minimum variance portfolio? The expected return of the portfolio is given by: E[rp] = (0.5) 20 + (0.5) 10 = 15% The variance of the portfolio can be calculated as (0.5)2(20)2 + (0.5)2(16)2 + 2(0.5)(0.5)(0.5)(20)(16) = 244 So, the standard deviation is 15.62% Recall that Asset 2 has an expected return of 10% and a standard deviation of 16%. Clearly this portfolio of equal weights in Asset 1 and Asset 2 is preferred to holding Asset 2 by itself since the portfolio has an expected return of 15% and a standard deviation of 15.62%. One way to find the minimum variance portfolio is to allow the weight to vary between 0 and 1 (from no investment in Asset 1 to all of our wealth in Asset 1) and examine the resulting portfolio. The expected returns and standard deviation of rates of return are as follows:
From this table we conclude that the minimum variance portfolio is given by setting w1 equal to (roughly) 0.3, that is investing 30% in Asset 1 and 70% in Asset 2. An alternative way to find the minimum variance portfolio is to use the result established above. Therefore, the minimum variance portfolio in this case is
With 28.57 percent of our wealth in Asset 1 and 71.43 percent of our wealth in Asset 2, the expected portfolio return is 12.86% and the standard deviation of the portfolio return is 15.12%. |
7.32 Risk Aversion and Portfolio Choice
We have talked about efficient portfolios being determined by the investors' preferences for more return to less return and less risk to more risk. Now let's consider individual investors. All investors are assumed to be risk averse and like more to less. On the following page the efficient frontier is drawn and a set of indifference curves for an investor. The optimal portfolio for this particular investor is at the point of tangency between the indifference curve and the efficient frontier. [Note the indifference curves can never be tangent to the inefficient portion of the frontier].

Figure 16
This is the optimal portfolio for one particular individual. Another person may be less tolerant of risk or very risk averse. This person's indifference curves are drawn below. Note that the optimal portfolio for this person has the smallest possible standard deviation.

Figure 17
The next graph shows a set of indifference curves for a person that has high risk tolerance or low risk aversion. Note that this does not mean that the person is a risk lover. The utility function is still concave (risk aversion) but it is close to linear for very low risk aversion. The tangency point on the indifference map shows this person choosing an efficient portfolio that has a large standard deviation compared to the other portfolios but note that the expected return is also higher.

Figure 18
7.33 Mean-Variance Geometry with a Risk Free Security
Now consider the introduction of a riskless security like a Treasury Bill. Suppose we invest in a combination of a portfolio on the efficient set (derived without the riskless security) and the riskless security. We can calculate the expected return and the standard deviation on this new portfolio.
E[rp] = (1-w) Rf + w Ee (Eq 11)
![]() (Eq
12)
(Eq
12)
Where Rf represents the risk free security, Ee represents the expected return of the portfolio on the efficient frontier and w is the proportion of funds invested in the risky security.

Figure 19
It is clear that the only portfolio on the old efficient frontier that is desirable is the tangency portfolio. If we chose another portfolio like A or B, this opportunity set is not efficient because for a given variance, you do not maximize the expected return.

Figure 20
Now, I mentioned the old efficient frontier and it is time to clarify what this means. By introducing a new security, the riskfree security, we have to redraw the efficient set. It turns out that the new efficient set is the straight line from the riskfree rate to the tangency portfolio and beyond. If you are on the line to the right of the tangency portfolio, you are borrowing at the riskfree rate (note we are assuming that borrowing and lending rates are the same) and investing in the tangency portfolio. If you are at the point Rf on the y-axis, this means that you have none your money (w = 0) in the risky asset. If you are at the point M, then all of your money is in the portfolio of risky assets (w = 1) -- which is the tangency portfolio. The line that forms this new efficient set is called the Capital Market Line.
So with a risky asset, there is only one optimal combination of risky investments for each investor. Diagrams are provided that show the optimal portfolio choice for individuals of average, low and high risk tolerance. The optimal portfolio is the tangency of the indifference curve to the efficient set.

Figure 21

Figure 22
If all investors agree upon Ee, ![]() and Rf then that optimal risky asset mix is the same
for all (and must be the market portfolio). This is a fundamental point
and provides the basis for the asset pricing theory. The implication
is that only two funds are held by every investor: a fund comprised of
the riskfree instrument and a fund which is the market portfolio. We call
this the 2 fund theorem. If people agree on the expected returns and variance-covariance
matrix, then they will see the same efficient frontier. With the riskfree
asset, there is only one portfolio of risky assets that is efficient. This
does not mean that the only investment portfolio that is held is M. We
know that people have differing degrees of risk aversion. What is implied
that there is only one portfolio of risky assets held in conjunction with
the riskfree asset. This portfolio of risky assets is the value weighted
market portfolio.
and Rf then that optimal risky asset mix is the same
for all (and must be the market portfolio). This is a fundamental point
and provides the basis for the asset pricing theory. The implication
is that only two funds are held by every investor: a fund comprised of
the riskfree instrument and a fund which is the market portfolio. We call
this the 2 fund theorem. If people agree on the expected returns and variance-covariance
matrix, then they will see the same efficient frontier. With the riskfree
asset, there is only one portfolio of risky assets that is efficient. This
does not mean that the only investment portfolio that is held is M. We
know that people have differing degrees of risk aversion. What is implied
that there is only one portfolio of risky assets held in conjunction with
the riskfree asset. This portfolio of risky assets is the value weighted
market portfolio.
Consider investment in a riskless asset with a return of Rf
and standard deviation of zero and a risky asset with mean return
of Ee and standard deviation of ![]() .
Let the portfolio weight for the risky asset be w and the portfolio
weight for the risk free asset must be 1-w. Now let's calculate
the portfolio mean and standard deviation. We know the formulas for the
portfolio mean and standard deviation for two assets:
.
Let the portfolio weight for the risky asset be w and the portfolio
weight for the risk free asset must be 1-w. Now let's calculate
the portfolio mean and standard deviation. We know the formulas for the
portfolio mean and standard deviation for two assets:
E[rp] = (1-w) Rf + w Ee
![]()
We can also write the expected returns equation as:
E[rp] = Rf + w (Ee - Rf )
But we know from the standard deviation equation:
![]()
Substitute this formula for w into the expected returns equation.
![]()
The term
![]()
is called the Sharpe Measure [Named after [William Sharpe] It is used to evaluate investments. Below is a graph depicting the expected return--standard deviation space. The Sharpe measure is the slope of the line from Rf (rise is (E-Rf) over run which is STD). The intercept is the riskfree rate, Rf.

Figure 23
The higher the Sharpe measure is the better the security looks. On the graph we could combine a strategy of borrowing and buying portfolio A to achieve the same expected return as portfolio B with a much smaller variance.
Let's consider a specific example. Suppose:

Just looking at portfolio A and B it is unclear which is the best investment. B has the higher return -- but it also has a higher variance. Let's first consider the Sharpe measures:

The measure suggests that portfolio B is dominated by a strategy of borrowing and holding portfolio A. Let's check this out by calculating the standard deviation of a levered portfolio of A that has exactly the same expected return as B:
0.25 = w (0.20) + (1-w) 0.08
Solving for weight w:
w = 0.17/0.12 = 1.4167
This suggests that a strategy of investing 141.67% of your money in A and borrowing 41.67% at the rate of Rf = 8% will deliver a portfolio return of 25% which is exactly the portfolio return for B. Now lets check the standard deviation of this levered portfolio:
![]()
Note that the other terms in the portfolio variance drop out because the variance of the riskfree asset is zero. We are left with a portfolio standard deviation of 28.33% which is lower than the 30% for portfolio B. The levered portfolio that contains A has the same mean as B but a lower standard deviation. As a result, the levered portfolio with A is preferred to the investment in B.
We can expand the analysis to include the all asset available in the market. We showed last time that only the positively sloped portion of the minimum variance frontier of risky assets satisfied our portfolio selection rules. Now let's introduce the riskfree asset into the analysis. We can use the tools that we developed above the discriminate among the portfolios on the efficient frontier of risky assets. We will search for combination of the riskfree asset and some risky portfolio that delivers the highest Sharpe measure. We know that the Sharpe measure is just the slope of the line that is drawn from the riskfree rate on the expected return axis. The portfolio with the highest Sharpe measure is the tangency portfolio.
So the best possible mean and standard deviation combinations are from the riskless and tangency portfolio. If 100% of your wealth is invested in the riskless asset, then your return is Rf and the standard deviation is zero. If 50% of your wealth is invested in the riskless asset and 50% of your wealth is in the tangency portfolio, then your portfolio lies in between R_f and M on the straight line. If 100% of your money is in the tangency portfolio, the your expected return is the expected return on the tangency portfolio and your standard deviation is the standard deviation on the tangency portfolio. Finally, if you borrow money at the riskless rate and combine your borrowing with your initial wealth to buy the tangency portfolio, then your portfolio is to the right of M on the straight line. This straight line is called the Capital Market Line.
Since total lending equals total borrowing in the economy, the tangency portfolio is the market portfolio. The market portfolio represents total invested wealth in risky assets. It is a portfolio with weights defined to be the total value of the asset divided by the total value of all risky assets. These weights are referred to as value weights.

Figure 24
Click here for a supplemental discussion and mathematical derivation of optimal portfolio choice.
7.35 Common Sense Diversification
Whereas the benefits of diversification can be achieved through random selection of a number of stocks, a number of common sense procedures can be usefully employed to construct a diversified portfolio. For example: