In [1]:

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import scipy.linalg as la

In [2]:

np.set_printoptions(formatter={'float': '{: 0.1f}'.format})

In [3]:

np.random.seed(123)

In [4]:

%load_ext rpy2.ipython

In [5]:

import pandas as pd

Applications of SVD

Reconstruction

In [6]:

iris = %R iris

In [7]:

X  = iris.iloc[:, :-1].values

In [8]:

X[:5]

Out[8]:

array([[ 5.1,  3.5,  1.4,  0.2],
       [ 4.9,  3.0,  1.4,  0.2],
       [ 4.7,  3.2,  1.3,  0.2],
       [ 4.6,  3.1,  1.5,  0.2],
       [ 5.0,  3.6,  1.4,  0.2]])

In [9]:

U, s, Vt = la.svd(X, full_matrices=False)

In [10]:

U.shape, s.shape, Vt.shape

Out[10]:

((150, 4), (4,), (4, 4))

In [11]:

(U @ np.diag(s) @ Vt)[:5]

Out[11]:

array([[ 5.1,  3.5,  1.4,  0.2],
       [ 4.9,  3.0,  1.4,  0.2],
       [ 4.7,  3.2,  1.3,  0.2],
       [ 4.6,  3.1,  1.5,  0.2],
       [ 5.0,  3.6,  1.4,  0.2]])

PCA

Center the data

In [12]:

Xc = X - X.mean(0)

In [13]:

Xc[:5]

Out[13]:

array([[-0.7,  0.4, -2.4, -1.0],
       [-0.9, -0.1, -2.4, -1.0],
       [-1.1,  0.1, -2.5, -1.0],
       [-1.2,  0.0, -2.3, -1.0],
       [-0.8,  0.5, -2.4, -1.0]])

Find SVD

In [14]:

U, s, Vt = la.svd(Xc, full_matrices=False)

PCA is \(U \Sigma\)

In [15]:

Y = U[:, :2] @ np.diag(s[:2])

In [16]:

plt.scatter(Y[:, 0], Y[:, 1],
            c=iris['Species'].astype('category').cat.codes)
plt.xlabel('PC1')
plt.ylabel('PC2')
pass
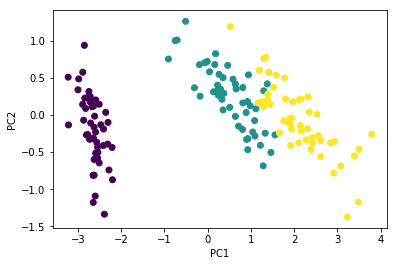
_images/S12B_SVD_Applications_21_0.png

PCA is also \(XV\)

In [17]:

Z = X @ Vt.T[:, :2]

In [18]:

plt.scatter(Z[:, 0], Z[:, 1],
            c=iris['Species'].astype('category').cat.codes)
plt.xlabel('PC1')
plt.ylabel('PC2')
pass
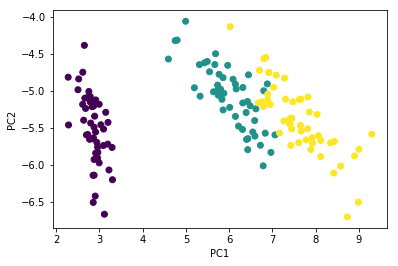
_images/S12B_SVD_Applications_24_0.png

Check with PCA routine. It should be the same (eigenvectors may flip)

In [19]:

from sklearn.decomposition import PCA

In [20]:

pca = PCA(n_components=2)

In [21]:

Y1 = pca.fit_transform(Xc)

In [22]:

plt.scatter(Y1[:, 0], Y1[:, 1],
            c=iris['Species'].astype('category').cat.codes)
plt.xlabel('PC1')
plt.ylabel('PC2')
pass
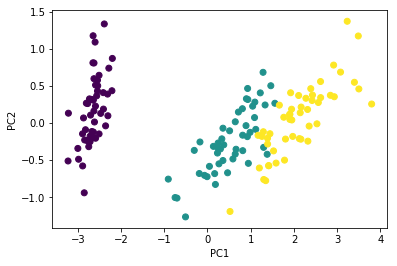
_images/S12B_SVD_Applications_29_0.png

Flip directions for the second eigenvector

In [60]:

plt.scatter(Y1[:, 0], -Y1[:, 1],
            c=iris['Species'].astype('category').cat.codes)
plt.xlabel('PC1')
plt.ylabel('PC2')
pass
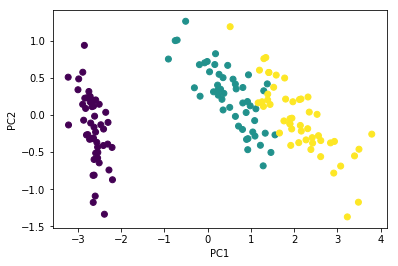
_images/S12B_SVD_Applications_31_0.png

Data compression (Low rank approximations)

In [23]:

X = np.ones((25, 15))
X[5:-5, 2:-2] = 0
X[8:-8, 6:-6] = 1

In [24]:

plt.imshow(X, cmap='gray')
pass
_images/S12B_SVD_Applications_34_0.png 
In [25]:

U, s, Vt = la.svd(X, full_matrices=False)

Note that tehre are only 3 types of columns, and so 3 singular values suffice to capture all the information.

In [26]:

np.cumsum(s)/s.sum()

Out[26]:

array([ 0.6,  0.9,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,
        1.0,  1.0,  1.0,  1.0])

In [27]:

X1 = U[:, :3] @ np.diag(s[:3]) @ Vt[:3, :]

In [28]:

plt.imshow(X, cmap='gray')
pass
_images/S12B_SVD_Applications_39_0.png

Using MNIST example

In [29]:

mnist = pd.read_csv('https://pjreddie.com/media/files/mnist_test.csv')

In [30]:

mnist.shape

Out[30]:

(9999, 785)

In [31]:

img = mnist.iloc[0, :-1].values.reshape((28,28))

In [32]:

plt.imshow(img, cmap='gray')
pass
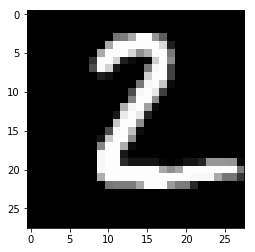
_images/S12B_SVD_Applications_44_0.png 
In [33]:

U, s, Vt = la.svd(img, full_matrices=False)

In [34]:

img1 = U[:, :1] @ np.diag(s[:1]) @ Vt[:1, :]

In [35]:

plt.imshow(img1, cmap='gray')
pass
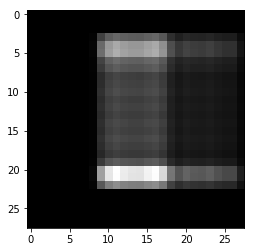
_images/S12B_SVD_Applications_47_0.png 
In [36]:

np.cumsum(s)/s.sum()

Out[36]:

array([ 0.3,  0.5,  0.6,  0.7,  0.8,  0.9,  0.9,  0.9,  0.9,  0.9,  1.0,
        1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,
        1.0,  1.0,  1.0,  1.0,  1.0,  1.0])

In [37]:

k = 6
imgk = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]

In [38]:

plt.imshow(imgk, cmap='gray')
pass
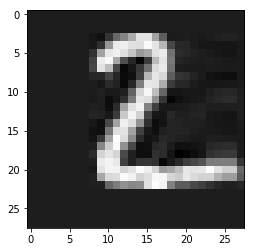
_images/S12B_SVD_Applications_50_0.png

We get slightly more than 50% compression with \(k=6\). Note that there are better methods for image compression.

In [39]:

sizes = (U[:, :k].size, s[:k].size, Vt[:k, :].size)

In [40]:

sizes

Out[40]:

(168, 6, 168)

In [41]:

img.size

Out[41]:

784

In [42]:

sum(sizes)

Out[42]:

342

Denoising

SVD by itself can do some denoising, but effective use requires more sophisticated algorithms such as k-SVD

In [43]:

img_noise = np.clip(img + np.random.normal(0, 30, img.shape), 0, 255)

In [44]:

plt.imshow(img_noise, cmap='gray')
pass
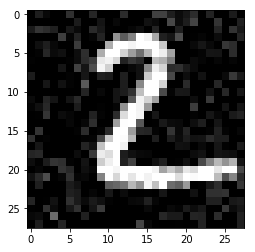
_images/S12B_SVD_Applications_58_0.png 
In [45]:

U, s, Vt = la.svd(img_noise, full_matrices=False)

In [46]:

np.cumsum(s)/s.sum()

Out[46]:

array([ 0.3,  0.4,  0.5,  0.6,  0.7,  0.7,  0.7,  0.8,  0.8,  0.8,  0.8,
        0.9,  0.9,  0.9,  0.9,  0.9,  0.9,  0.9,  1.0,  1.0,  1.0,  1.0,
        1.0,  1.0,  1.0,  1.0,  1.0,  1.0])

In [47]:

k = 6
imgk_noise = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]

In [48]:

plt.imshow(imgk_noise, cmap='gray')
pass
_images/S12B_SVD_Applications_62_0.png

Recommender system

Based on toy example from this blog post

In [49]:

from collections import OrderedDict

We have a database of movies and user ratings, but since most users watch and rate only a small subset of all possible movies, there is a lot of missing data. Our job is to predict what other movies a user might like, based on the movies that the user has rated.

Recall that SVD gives the optimal (in terms of Frobenius norm) low rank reconstruction for a matrix. This is true even for sparse matrices, and we make use of this to make predictions about user movie preferences.

Note: Real world recommender systems based on SVD calculate an approximate SVD using iterative methods for computational efficiency, but the idea is the same - we assume that the data can be modeled by \(k\) latent factors, then reconstruct the rank-\(k\) matrix. You’d also normalize the data in a real-use case.

In [50]:

ratings = pd.SparseDataFrame.from_dict(OrderedDict(
    A = [2,None,2,4,5,None],
    B = [5,None,4,None,None,1],
    C = [None,None,5,None,2,None],
    D = [None,1,None,5,None,4],
    E = [None,None,4,None,None,2,],
    F = [4,5,None,1,None,None]), orient='index'
)
ratings.columns = ['The Avengers', 'Sherlock', 'Transformers', 'Matrix', 'Titanic', 'Me Before You']

In [51]:

ratings

Out[51]:
The Avengers Sherlock Transformers Matrix Titanic Me Before You
A 2.0 NaN 2.0 4.0 5.0 NaN
B 5.0 NaN 4.0 NaN NaN 1.0
C NaN NaN 5.0 NaN 2.0 NaN
D NaN 1.0 NaN 5.0 NaN 4.0
E NaN NaN 4.0 NaN NaN 2.0
F 4.0 5.0 NaN 1.0 NaN NaN

We need to deal with the sparsity.

In [52]:

from scipy.sparse.linalg import svds

In [53]:

X = ratings.to_coo()

In [54]:

print(X)

  (0, 0)        2.0
  (1, 0)        5.0
  (5, 0)        4.0
  (3, 1)        1.0
  (5, 1)        5.0
  (0, 2)        2.0
  (1, 2)        4.0
  (2, 2)        5.0
  (4, 2)        4.0
  (0, 3)        4.0
  (3, 3)        5.0
  (5, 3)        1.0
  (0, 4)        5.0
  (2, 4)        2.0
  (1, 5)        1.0
  (3, 5)        4.0
  (4, 5)        2.0

In [55]:

U, s, Vt = svds(X, k=min(ratings.shape)-1)

In [56]:

s

Out[56]:

array([ 3.0,  4.9,  6.4,  6.9,  10.1])

svds gives singular values in ascending order, so we need to perform a permutation to get it in the fmiliar form.

In [57]:

perm = np.arange(len(s))[::-1]
U = U[:, perm]
s = s[perm]
Vt = Vt[perm, :]

In [58]:

k = 3
Y = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]
Y

Out[58]:

array([[ 1.4,  0.4,  2.9,  4.0,  2.7,  2.1],
       [ 4.0,  1.5,  4.2, -0.2,  1.0,  0.2],
       [ 0.9, -1.1,  4.6,  0.0,  1.8,  0.4],
       [ 0.3,  1.0, -0.6,  5.0,  1.9,  2.3],
       [ 0.7, -0.7,  3.3,  0.2,  1.4,  0.4],
       [ 4.7,  4.0, -0.2,  1.1, -0.5,  0.4]])

In [59]:

user = 'E'
pd.DataFrame(OrderedDict(
    Observed = ratings.loc[user].to_dense(),
    Predicted = Y[ratings.index.tolist().index(user)]))

Out[59]:
Observed Predicted
The Avengers NaN 0.749016
Sherlock NaN -0.688250
Transformers 4.0 3.292351
Matrix NaN 0.243724
Titanic NaN 1.360181
Me Before You 2.0 0.379015