Time Series Analysis 1

In the first lecture, we are mainly concerned with how to manipulate and smooth time series data.

In [1]:

%matplotlib inline
import matplotlib.pyplot as plt

In [2]:

import os
import time

In [3]:

import numpy as np
import pandas as pd

In [4]:

import gmaps
import gmaps.datasets

Dates and times

Timestamps

In [5]:

now = pd.to_datetime('now')

In [6]:

now

Out[6]:

Timestamp('2018-11-04 17:15:19.437536')

In [7]:

now.year, now.month, now.week, now.day, now.hour, now.minute, now.second, now.microsecond

Out[7]:

(2018, 11, 44, 4, 17, 15, 19, 437536)

In [8]:

now.month_name(), now.day_name()

Out[8]:

('November', 'Sunday')

Formatting timestamps

See format codes

In [9]:

now.strftime('%I:%m%p %d-%b-%Y')

Out[9]:

'05:11PM 04-Nov-2018'

Parsing time strings

pandas can handle standard formats

In [10]:

ts = pd.to_datetime('6-Dec-2018 4:45 PM')

In [11]:

ts

Out[11]:

Timestamp('2018-12-06 16:45:00')

For unusual formats, use strptime

In [12]:

ts = pd.datetime.strptime('10:11PM 02-Nov-2018', '%I:%m%p %d-%b-%Y')

In [13]:

ts

Out[13]:

datetime.datetime(2018, 11, 2, 22, 0)

Intervals

In [14]:

then = pd.to_datetime('now')
time.sleep(5)
now = pd.to_datetime('now')

In [15]:

now - then

Out[15]:

Timedelta('0 days 00:00:05.004077')

Date ranges

A date range is just a collection of time stamps.

In [16]:

dates = pd.date_range(then, now, freq='s')

In [17]:

dates

Out[17]:

DatetimeIndex(['2018-11-04 17:15:19.500621', '2018-11-04 17:15:20.500621',
               '2018-11-04 17:15:21.500621', '2018-11-04 17:15:22.500621',
               '2018-11-04 17:15:23.500621', '2018-11-04 17:15:24.500621'],
              dtype='datetime64[ns]', freq='S')

In [18]:

(then - pd.to_timedelta('1.5s')) in dates

Out[18]:

False

Periods

Periods are intervals, not a collection of timestamps.

In [19]:

span = dates.to_period()

In [20]:

span

Out[20]:

PeriodIndex(['2018-11-04 17:15:19', '2018-11-04 17:15:20',
             '2018-11-04 17:15:21', '2018-11-04 17:15:22',
             '2018-11-04 17:15:23', '2018-11-04 17:15:24'],
            dtype='period[S]', freq='S')

In [21]:

(then + pd.to_timedelta('1.5s')) in span

Out[21]:

True

Lag and lead with shift

We will use a periodic time series as an example. Periodicity is important because many biological phenomena are linked to natural periods (seasons, diurnal, menstrual cycle) or are intrinsically periodic (e.g. EEG, EKG measurements).

In [22]:

index = pd.date_range('1-1-2018', '31-1-2018', freq='12h')

You can shift by periods or by frequency. Shifting by frequency maintains boundary data.

In [23]:

wave = pd.Series(np.sin(np.arange(len(index))), index=index)

In [24]:

wave.shift(periods=1).head(3)

Out[24]:

2018-01-01 00:00:00         NaN
2018-01-01 12:00:00    0.000000
2018-01-02 00:00:00    0.841471
Freq: 12H, dtype: float64

In [25]:

wave.shift(periods=1).tail(3)

Out[25]:

2018-01-30 00:00:00    0.436165
2018-01-30 12:00:00    0.992873
2018-01-31 00:00:00    0.636738
Freq: 12H, dtype: float64

In [26]:

wave.shift(freq=1).head(3)

Out[26]:

2018-01-01 12:00:00    0.000000
2018-01-02 00:00:00    0.841471
2018-01-02 12:00:00    0.909297
Freq: 12H, dtype: float64

In [27]:

wave.shift(freq=1).tail(3)

Out[27]:

2018-01-30 12:00:00    0.992873
2018-01-31 00:00:00    0.636738
2018-01-31 12:00:00   -0.304811
Freq: 12H, dtype: float64

In [28]:

wave.plot()
pass
_images/S18A_Time_Series_Manipulation_Smoothing_40_0.png 
In [29]:

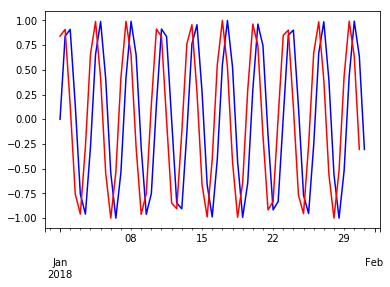
wave.plot(c='blue')
wave.shift(-1).plot(c='red')
pass
_images/S18A_Time_Series_Manipulation_Smoothing_41_0.png 
In [30]:

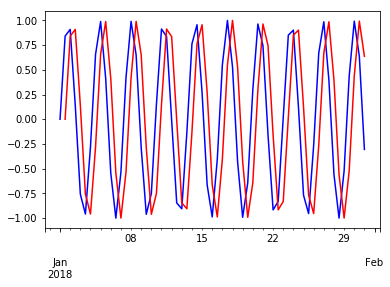
wave.plot(c='blue')
wave.shift(1).plot(c='red')
pass
_images/S18A_Time_Series_Manipulation_Smoothing_42_0.png 
In [31]:

(wave - wave.shift(-6)).plot(c='blue')
(wave - wave.shift(-3)).plot(c='red')
pass
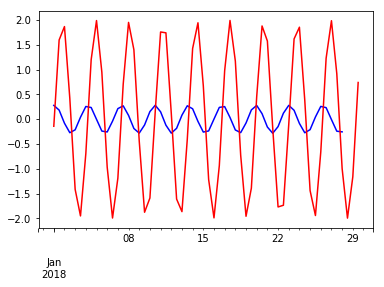
_images/S18A_Time_Series_Manipulation_Smoothing_43_0.png

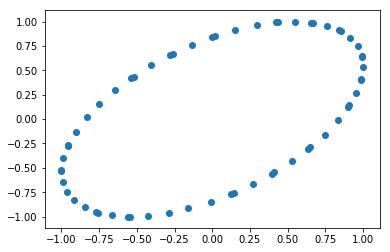
Embedding the time series with its lagged version reveals its periodic nature.

In [32]:

plt.scatter(wave, wave.shift(-1))
pass
_images/S18A_Time_Series_Manipulation_Smoothing_45_0.png

Find percent change from previous period

In [33]:

wave.pct_change().head()

Out[33]:

2018-01-01 00:00:00         NaN
2018-01-01 12:00:00         inf
2018-01-02 00:00:00    0.080605
2018-01-02 12:00:00   -0.844803
2018-01-03 00:00:00   -6.362829
Freq: 12H, dtype: float64

pct_change is just a convenience wrapper around the use of shift

In [34]:

((wave - wave.shift(-1, freq='12h'))/wave).head()

Out[34]:

2017-12-31 12:00:00         NaN
2018-01-01 00:00:00        -inf
2018-01-01 12:00:00   -0.080605
2018-01-02 00:00:00    0.844803
2018-01-02 12:00:00    6.362829
Freq: 12H, dtype: float64

Resampling and window functions

The resample and window method have the same syntax as groupby, in that you can apply an aggregate function to the new intervals.

Resampling

Sometimes there is a need to generate new time intervals, for example, to regularize irregularly timed observations.

Down-sampling

In [35]:

index = pd.date_range(pd.to_datetime('1-1-2018'), periods=365, freq='d')

In [36]:

series = pd.Series(np.arange(len(index)), index=index)

In [37]:

series.head()

Out[37]:

2018-01-01    0
2018-01-02    1
2018-01-03    2
2018-01-04    3
2018-01-05    4
Freq: D, dtype: int64

In [38]:

sereis_weekly_average = series.resample('w').mean()
sereis_weekly_average.head()

Out[38]:

2018-01-07     3
2018-01-14    10
2018-01-21    17
2018-01-28    24
2018-02-04    31
Freq: W-SUN, dtype: int64

In [39]:

sereis_monthly_sum = series.resample('m').sum()
sereis_monthly_sum.head()

Out[39]:

2018-01-31     465
2018-02-28    1246
2018-03-31    2294
2018-04-30    3135
2018-05-31    4185
Freq: M, dtype: int64

In [40]:

sereis_10day_median = series.resample('10d').median()
sereis_10day_median.head()

Out[40]:

2018-01-01     4.5
2018-01-11    14.5
2018-01-21    24.5
2018-01-31    34.5
2018-02-10    44.5
dtype: float64

Up-sampling

For up-sampling, we need to figure out what we want to do with the missing values. The usual choices are forward fill, backward fill, or interpolation using one of many built-in methods.

In [41]:

upsampled = series.resample('12h')

In [42]:

upsampled.asfreq()[:5]

Out[42]:

2018-01-01 00:00:00    0.0
2018-01-01 12:00:00    NaN
2018-01-02 00:00:00    1.0
2018-01-02 12:00:00    NaN
2018-01-03 00:00:00    2.0
Freq: 12H, dtype: float64

In [43]:

upsampled.ffill().head()

Out[43]:

2018-01-01 00:00:00    0
2018-01-01 12:00:00    0
2018-01-02 00:00:00    1
2018-01-02 12:00:00    1
2018-01-03 00:00:00    2
Freq: 12H, dtype: int64

In [44]:

upsampled.bfill().head()

Out[44]:

2018-01-01 00:00:00    0
2018-01-01 12:00:00    1
2018-01-02 00:00:00    1
2018-01-02 12:00:00    2
2018-01-03 00:00:00    2
Freq: 12H, dtype: int64

In [45]:

upsampled.interpolate('linear').head()

Out[45]:

2018-01-01 00:00:00    0.0
2018-01-01 12:00:00    0.5
2018-01-02 00:00:00    1.0
2018-01-02 12:00:00    1.5
2018-01-03 00:00:00    2.0
Freq: 12H, dtype: float64

Window functions

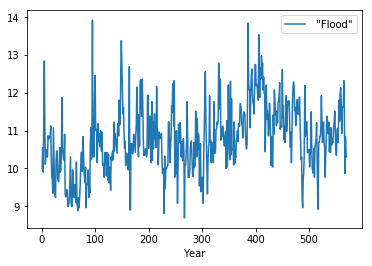
Window functions are typically used to smooth time series data. There are 3 variants - rolling, expanding and exponentially weighted. We use the Nile flooding data for these examples.

In [46]:

df = pd.read_csv('data/nile.csv', index_col=0)

In [47]:

df.head()

Out[47]:
"Flood"
Year
1 9.9974
2 10.5556
3 9.9014
4 11.4800
5 12.8460 
In [48]:

df.plot()
pass
_images/S18A_Time_Series_Manipulation_Smoothing_68_0.png

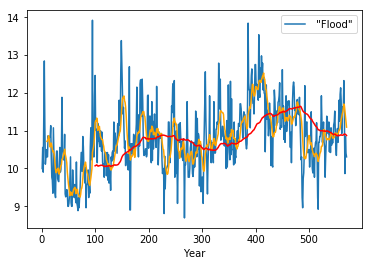
Rolling windows generate windows of a specified width

In [49]:

ts = pd.DataFrame(dict(ts=np.arange(5)))
ts['rolling'] = ts.rolling(window=3).sum()
ts

Out[49]:
ts rolling
0 0 NaN
1 1 NaN
2 2 3.0
3 3 6.0
4 4 9.0 
In [50]:

rolling10 = df.rolling(window=10)
rolling100 = df.rolling(window=100)

In [51]:

df.plot()
plt.plot(rolling10.mean(), c='orange')
plt.plot(rolling100.mean(), c='red')
pass
_images/S18A_Time_Series_Manipulation_Smoothing_72_0.png

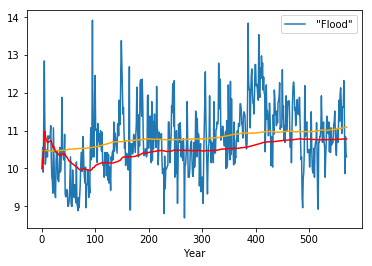
Expanding windows grow as the time series progresses

In [52]:

ts['expanding'] =  ts.ts.expanding().sum()
ts

Out[52]:
ts rolling expanding
0 0 NaN 0.0
1 1 NaN 1.0
2 2 3.0 3.0
3 3 6.0 6.0
4 4 9.0 10.0 
In [53]:

df.plot()
plt.plot(df.expanding(center=True).mean(), c='orange')
plt.plot(df.expanding().mean(), c='red')
pass
_images/S18A_Time_Series_Manipulation_Smoothing_75_0.png

Exponentially weighted windows place more weight on center of mass

In [54]:

n = 10
xs = np.arange(n, dtype='float')[::-1]
xs

Out[54]:

array([9., 8., 7., 6., 5., 4., 3., 2., 1., 0.])

Exponentially weighted windows without adjustment.

In [55]:

pd.Series(xs).ewm(alpha=0.8, adjust=False).mean()

Out[55]:

0    9.000000
1    8.200000
2    7.240000
3    6.248000
4    5.249600
5    4.249920
6    3.249984
7    2.249997
8    1.249999
9    0.250000
dtype: float64

Re-implementation for insight.

In [56]:

α = 0.8
ys = np.zeros_like(xs)
ys[0] = xs[0]
for i in range(1, len(xs)):
    ys[i] = (1-α)*ys[i-1] + α*xs[i]
ys

Out[56]:

array([9.        , 8.2       , 7.24      , 6.248     , 5.2496    ,
       4.24992   , 3.249984  , 2.2499968 , 1.24999936, 0.24999987])

Exponentially weighted windows with adjustment (default)

In [57]:

pd.Series(xs).ewm(alpha=0.8, adjust=True).mean()

Out[57]:

0    9.000000
1    8.166667
2    7.225806
3    6.243590
4    5.248399
5    4.249616
6    3.249910
7    2.249980
8    1.249995
9    0.249999
dtype: float64

Re-implementation for insight.

In [58]:

α = 0.8
ys = np.zeros_like(xs)
ys[0] = xs[0]
for i in range(1, len(xs)):
    ws = np.array([(1-α)**(i-t) for t in range(i+1)])
    ys[i] = (ws * xs[:len(ws)]).sum()/ws.sum()
ys

Out[58]:

array([9.        , 8.16666667, 7.22580645, 6.24358974, 5.24839949,
       4.24961598, 3.2499104 , 2.24997952, 1.24999539, 0.24999898])

In [59]:

df.plot()
plt.plot(df.ewm(alpha=0.8).mean(), c='orange')
plt.plot(df.ewm(alpha=0.2).mean(), c='red')
pass
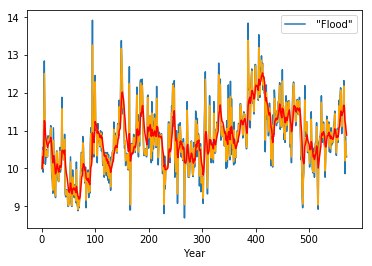
_images/S18A_Time_Series_Manipulation_Smoothing_86_0.png

Alternatives to \(\alpha\)

Using span

\[\alpha = \frac{2}{\text{span} + 1}\]

Using halflife

\[\alpha = 1 - e^\frac{-\log{2}}{t_{1/2}}\]

Using com

\[\alpha = \frac{1}{1 + \text{com}}\]
In [60]:

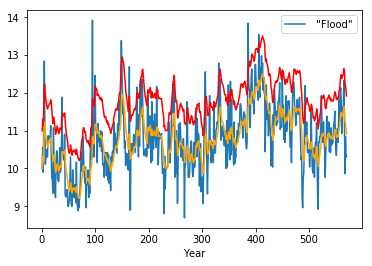
df.plot()
plt.plot(df.ewm(span=10).mean(), c='orange')
plt.plot(1+ df.ewm(alpha=2/11).mean(), c='red') # offfset for visibility
pass
_images/S18A_Time_Series_Manipulation_Smoothing_89_0.png

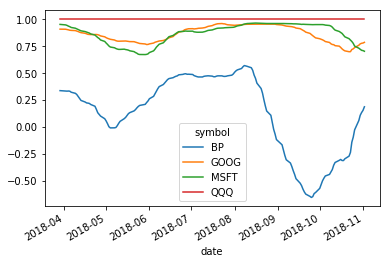
Correlation between time series

Suppose we had a reference time series. It is often of interest to know how any particular time series is correlated with the reference. Often the reference might be a population average, and we want to see where a particular time series deviates in behavior.

In [61]:

import pandas_datareader.data as web

We will look at the correlation of some stocks.

QQQ tracks Nasdaq
MSFT is Microsoft
GOOG is Gogole
BP is British Petroleum

We expect that the technology stocks should be correlated with Nasdaq, but maybe not BP.

In [62]:

df = web.DataReader(['QQQ', 'MSFT','GOOG', 'BP'], 'robinhood')

In [63]:

df = df[['close_price']]

In [64]:

df = df.unstack(level=0)

In [65]:

df.columns = df.columns.get_level_values(1)

In [66]:

df.index.name = 'date'

In [67]:

df.index = pd.to_datetime(df.index)

In [68]:

df.head()

Out[68]:
symbol BP GOOG MSFT QQQ
date
2017-11-03 38.839900 1032.480000 82.643000 152.102400
2017-11-06 39.653900 1025.900000 82.967200 152.618500
2017-11-07 39.720900 1033.330000 82.770700 152.707800
2017-11-08 39.644300 1039.850000 83.055600 153.323100
2017-11-09 39.582200 1031.260000 82.593900 152.519200 
In [69]:

df.rolling(100).corr(df.QQQ).plot()
pass
_images/S18A_Time_Series_Manipulation_Smoothing_100_0.png

Visualizing space and time data

Being able to visualize events in space and time can be impressive. With Python, often you need a trivial amount of code to produce an impressive visualization.

For example, lets generate a heatmap of crimes in Sacramento in 2006, and highlight the crimes committed 10 seconds before midnight.

See the gmaps package for more information.

In [70]:

sacramento_crime = pd.read_csv('data/SacramentocrimeJanuary2006.csv', index_col=0)

In [71]:

sacramento_crime.index = pd.to_datetime(sacramento_crime.index)

In [72]:

sacramento_crime.head()

Out[72]:
address district beat grid crimedescr ucr_ncic_code latitude longitude
cdatetime
2006-01-01 3108 OCCIDENTAL DR 3 3C 1115 10851(A)VC TAKE VEH W/O OWNER 2404 38.550420 -121.391416
2006-01-01 2082 EXPEDITION WAY 5 5A 1512 459 PC BURGLARY RESIDENCE 2204 38.473501 -121.490186
2006-01-01 4 PALEN CT 2 2A 212 10851(A)VC TAKE VEH W/O OWNER 2404 38.657846 -121.462101
2006-01-01 22 BECKFORD CT 6 6C 1443 476 PC PASS FICTICIOUS CHECK 2501 38.506774 -121.426951
2006-01-01 3421 AUBURN BLVD 2 2A 508 459 PC BURGLARY-UNSPECIFIED 2299 38.637448 -121.384613 
In [73]:

gmaps.configure(api_key=os.environ["GOOGLE_API_KEY"])

In [74]:

locations = sacramento_crime[['latitude', 'longitude']]

In [75]:

late_locations = sacramento_crime.between_time('23:59', '23:59:59')[['latitude', 'longitude']]

In [76]:

fig = gmaps.figure()
fig.add_layer(gmaps.heatmap_layer(locations))
markers = gmaps.marker_layer(late_locations)
fig.add_layer(markers)
fig