Functions¶
In [1]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Waht’s wrong with this code?¶
In [2]:
max_iter = 100
h, w = 400, 400
img = np.zeros((h, w)).astype('int')
for i, real in enumerate(np.linspace(-1.5, 0.5, w)):
for j, imag in enumerate(np.linspace(-1, 1, h)):
c = complex(real, imag)
z = 0 + 0j
for k in range(max_iter):
z = z*z + c
if abs(z) > 2:
break
img[j, i] = k
plt.grid(False)
plt.imshow(img, cmap=plt.cm.jet)
pass
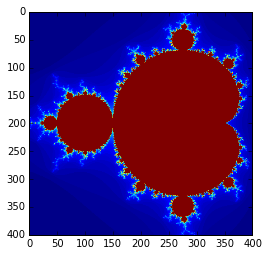
- hard to udnerstand
- uses global variabels
- not re-usable except by copy and paste
Refactoring to use functions¶
In [3]:
def mandel(c, z=0, max_iter=100):
for k in range(max_iter):
z = z*z + c
if abs(z) > 2:
return k
return k
In [4]:
def mandelbrot(w, h, xl=-1.5, xu=0.5, yl=-1, yu=1):
img = np.zeros((h, w)).astype('int')
for i, real in enumerate(np.linspace(xl, xu, w)):
for j, imag in enumerate(np.linspace(yl, yu, h)):
c = complex(real, imag)
img[j, i] = mandel(c)
return img
In [5]:
img = mandelbrot(w=400, h=400)
plt.grid(False)
plt.imshow(img, cmap=plt.cm.jet)
pass
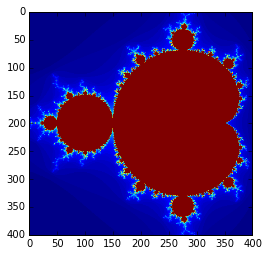
Function is re-usable¶
In [6]:
img = mandelbrot(w=400, h=400, xl=-0.75, xu=-0.73, yl=0.1, yu=0.12)
plt.grid(False)
plt.imshow(img, cmap=plt.cm.jet)
pass
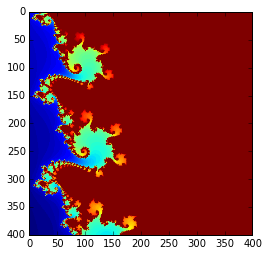
Anonlymous functions (lamabdas)¶
In [7]:
def square(x):
return x*x
In [8]:
square(3)
Out[8]:
9
In [9]:
square2 = lambda x: x*x
In [10]:
square2(3)
Out[10]:
9
First class functions¶
In [11]:
# functions can be traated the same way as (say) an integer
Fnctions can be passed in as arguments¶
In [12]:
def grad(x, f, h=0.01):
return (f(x+h) - f(x-h))/(2*h)
In [13]:
def f(x):
return 3*x**2 + 5*x + 3
In [14]:
grad(0, f)
Out[14]:
5.000000000000004
Funcitons can also be returned by functions¶
In [15]:
import time
def timer(f):
def g(*args, **kwargs):
start = time.clock()
result = f(*args, **kwargs)
elapsed = time.clock() - start
return result, elapsed
return g
In [16]:
def f(n=1000000):
s = sum([x*x for x in range(n)])
return s
timed_func = timer(f)
In [17]:
timed_func()
Out[17]:
(333332833333500000, 0.22118899999999897)
Decorators¶
In [18]:
@timer
def g(n=1000000):
s = sum([x*x for x in range(n)])
return s
In [19]:
g()
Out[19]:
(333332833333500000, 0.2040980000000001)
Map, filter, reduce¶
In [20]:
map(lambda x: x*x, [1,2,3,4])
Out[20]:
<map at 0x109246a90>
In [21]:
list(map(lambda x: x*x, [1,2,3,4]))
Out[21]:
[1, 4, 9, 16]
In [22]:
list(filter(lambda x: x%2==0, [1,2,3,4]))
Out[22]:
[2, 4]
In [23]:
from functools import reduce
In [24]:
reduce(lambda x, y: x*y, [1,2,3,4], 10)
Out[24]:
240
List comprehenision¶
In [25]:
[x*x for x in [1,2,3,4]]
Out[25]:
[1, 4, 9, 16]
In [26]:
[x for x in [1,2,3,4] if x%2 == 0]
Out[26]:
[2, 4]
Set and dictionary comprehension¶
In [27]:
{i%3 for i in range(10)}
Out[27]:
{0, 1, 2}
In [28]:
{i: i%3 for i in range(10)}
Out[28]:
{0: 0, 1: 1, 2: 2, 3: 0, 4: 1, 5: 2, 6: 0, 7: 1, 8: 2, 9: 0}
Generator expressions¶
In [29]:
(i**2 for i in range(10,15))
Out[29]:
<generator object <genexpr> at 0x1094cb938>
In [30]:
for x in (i**2 for i in range(10,15)):
print(x)
100
121
144
169
196
Generator expressions¶
Generator expressions return a potentially infinite stream, but one at a time thus sparing memory. They are ubiquitous in Python 3, allowing us to handle arbitrarily large data sets.
In [31]:
def count(i=0):
while True:
yield i
i += 1
In [32]:
c = count()
next(c)
Out[32]:
0
In [33]:
next(c)
Out[33]:
1
In [34]:
next(c)
Out[34]:
2
In [35]:
list(zip('abcde', count(10)))
Out[35]:
[('a', 10), ('b', 11), ('c', 12), ('d', 13), ('e', 14)]
Itertools¶
In [36]:
import itertools as it
In [37]:
for i in it.islice(count(), 5, 10):
print(i)
5
6
7
8
9
In [38]:
for i in it.takewhile(lambda i: i< 5, count()):
print(i)
0
1
2
3
4
In [39]:
import operator as op
[i for i in it.starmap(op.add, [(1,2), (2,3), (3,4)])]
Out[39]:
[3, 5, 7]
In [40]:
fruits = ['appple', 'banana', 'cherry', 'durain', 'eggplant', 'fig']
for k, group in it.groupby(sorted(fruits, key=len), len):
print(k, list(group))
3 ['fig']
6 ['appple', 'banana', 'cherry', 'durain']
8 ['eggplant']
Functools¶
In [41]:
import functools as fn
In [42]:
rng1 = fn.partial(np.random.normal, 2, .3)
rng2 = fn.partial(np.random.normal, 10, 1)
In [43]:
rng1(10)
Out[43]:
array([ 1.74912105, 1.98518135, 2.10565975, 1.74981538, 1.57383371,
2.17027087, 2.66615411, 2.17479635, 1.65850304, 2.18972124])
In [44]:
rng2(10)
Out[44]:
array([ 7.47878506, 11.1307094 , 9.95800128, 9.91753149,
8.93918569, 9.46457246, 11.96952595, 10.76935203,
11.74376052, 8.77382197])
In [45]:
fn.reduce(op.add, rng2(10))
Out[45]:
95.891256272508414
Modules¶
In [46]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
In [47]:
from pandas import DataFrame, Series
import scipy.stats as ss
In [48]:
DataFrame(ss.beta(2,5).rvs((3,4)), columns=['a', 'b', 'c', 'd'])
Out[48]:
| a | b | c | d | |
|---|---|---|---|---|
| 0 | 0.546453 | 0.066061 | 0.274397 | 0.062071 |
| 1 | 0.190301 | 0.126242 | 0.185920 | 0.591911 |
| 2 | 0.136587 | 0.190615 | 0.016919 | 0.157208 |
Where does Python search for modules?¶
In [49]:
import sys
sys.path
Out[49]:
['',
'/Users/cliburn/anaconda/envs/py35/lib/python35.zip',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/plat-darwin',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/lib-dynload',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/site-packages/Sphinx-1.3.1-py3.5.egg',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/site-packages/setuptools-19.1.1-py3.5.egg',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/site-packages',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/site-packages/aeosa',
'/Users/cliburn/anaconda/envs/py35/lib/python3.5/site-packages/IPython/extensions',
'/Users/cliburn/.ipython']
Creating your own module¶
In [50]:
%%file my_module.py
PI = 3.14
def my_f(x):
return PI*x
Overwriting my_module.py
In [51]:
import my_module as mm
mm.PI
Out[51]:
3.14
In [52]:
mm.my_f(2)
Out[52]:
6.28
In [53]:
from my_module import PI
In [54]:
PI * 2 * 2
Out[54]:
12.56
Note: Modules can also be nested within each other - e.g.
numpy.random to creaate a package. We will explore how to create
packages in a later session.