Scalars¶

In [1]:

%matplotlib inline

In [2]:

import numpy as np
import matplotlib.pyplot as plt

Integers¶

Binary representation of integers¶

In [3]:

format(16, '032b')

Out[3]:

'00000000000000000000000000010000'

Bit shifting¶

In [4]:

format(16 >> 2, '032b')

Out[4]:

'00000000000000000000000000000100'

In [5]:

16 >> 2

Out[5]:

In [6]:

format(16 << 2, '032b')

Out[6]:

'00000000000000000000000001000000'

In [7]:

16 << 2

Out[7]:

Overflow¶

In general, the computer representation of integers has a limited range, and may overflow. The range depends on whether the integer is signed or unsigned.

For example, with 8 bits, we can represent at most \(2^8 = 256\) integers.

0 to 255 unsigned
-128 ti 127 signed

Signed integers

In [8]:

np.arange(130, dtype=np.int8)[-5:]

Out[8]:

array([ 125,  126,  127, -128, -127], dtype=int8)

Unsigned integers

In [9]:

np.arange(130, dtype=np.uint8)[-5:]

Out[9]:

array([125, 126, 127, 128, 129], dtype=uint8)

In [10]:

np.arange(260, dtype=np.uint8)[-5:]

Out[10]:

array([255,   0,   1,   2,   3], dtype=uint8)

Integer division¶

In Python 2 or other languages such as C/C++, be very careful when dividing as the division operator / performs integer division when both numerator and denominator are integers. This is rarely what you want. In Python 3 the / always performs floating point division, and you use // for integer division, removing a common source of bugs in numerical calculations.

In [11]:

%%python2

import numpy as np

x = np.arange(10)
print(x/10)

[0 0 0 0 0 0 0 0 0 0]

Python 3 does the “right” thing.

In [12]:

x = np.arange(10)
x/10

Out[12]:

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

Real numbers¶

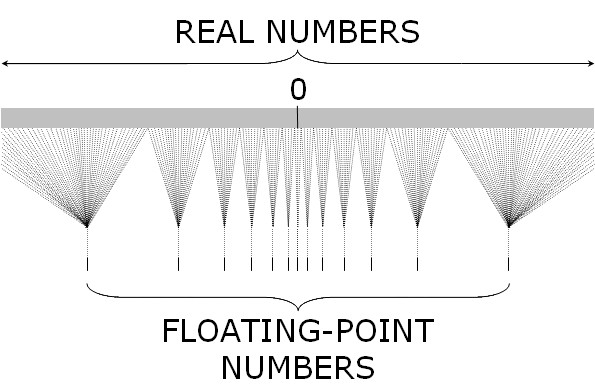
Real numbers are represented as floating point numbers. A floating point number is stored in 3 pieces (sign bit, exponent, mantissa) so that every float is represetned as get +/- mantissa ^ exponent. Because of this, the interval between consecutive numbers is smallest (high precison) for numebrs close to 0 and largest for numbers close to the lower and upper bounds.

Because exponents have to be singed to represent both small and large numbers, but it is more convenint to use unsigned numbers here, the exponnent has an offset (also knwnn as the exponentn bias). For example, if the expoennt is an unsigned 8-bit number, it can rerpesent the range (0, 255). By using an offset of 128, it will now represent the range (-127, 128).

float1¶

Note: Intervals between consecutive floating point numbers are not constant. In particular, the precision for small numbers is much larger than for large numbers. In fact, approximately half of all floating point numbers lie between -1 and 1 when using the double type in C/C++ (also the default for numpy).

float2¶

Because of this, if you are adding many numbers, it is more accurate to first add the small numbers before the large numbers.

img¶

See Wikipedia for how this binary number is evaluated to 0.15625.

In [13]:

from ctypes import c_int, c_float

In [14]:

s = c_int.from_buffer(c_float(0.15625)).value

In [15]:

s = format(s, '032b')
s

Out[15]:

'00111110001000000000000000000000'

In [16]:

rep = {
    'sign': s[:1],
    'exponent' : s[1:9:],
    'fraction' : s[9:]
}
rep

Out[16]:

{'sign': '0', 'exponent': '01111100', 'fraction': '01000000000000000000000'}

Most base 10 real numbers are approximations¶

This is simply because numbers are stored in finite-precision binary format.

In [17]:

'%.20f' % (0.1 * 0.1 * 100)

Out[17]:

'1.00000000000000022204'

Never check for equality of floating point numbers¶

In [18]:

i = 0
loops = 0
while i != 1:
    i += 0.1 * 0.1
    loops += 1
    if loops == 1000000:
        break
i

Out[18]:

10000.000000171856

In [19]:

i = 0
loops = 0
while np.abs(1 - i) > 1e-6:
    i += 0.1 * 0.1
    loops += 1
    if loops == 1000000:
        break
i

Out[19]:

1.0000000000000007

Associative law does not necessarily hold¶

In [20]:

6.022e23 - 6.022e23 + 1

Out[20]:

1.0

In [21]:

1 + 6.022e23 - 6.022e23

Out[21]:

0.0

Distributive law does not hold¶

In [22]:

a = np.exp(1)
b = np.pi
c = np.sin(1)

In [23]:

a*(b+c)

Out[23]:

10.82708950985241

In [24]:

a*b + a*c

Out[24]:

10.827089509852408

Catastrophic cancellation¶

Consider calculating sample variance

\[s^2= \frac{1}{n(n-1)}\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i)^2\]

Be careful whenever you calculate the difference of potentially big numbers.

In [25]:

def var(x):
    """Returns variance of sample data using sum of squares formula."""

    n = len(x)
    return (1.0/(n*(n-1))*(n*np.sum(x**2) - (np.sum(x))**2))

Underflow¶

In [26]:

np.warnings.filterwarnings('ignore')

In [27]:

np.random.seed(4)
xs = np.random.random(1000)
ys = np.random.random(1000)
np.prod(xs)/np.prod(ys)

Out[27]:

nan

Prevent underflow by staying in log space¶

In [28]:

x = np.sum(np.log(xs))
y = np.sum(np.log(ys))
np.exp(x - y)

Out[28]:

696432868222.2549

Overflow¶

In [29]:

np.exp(1000)

Out[29]:

inf

Numerically stable algorithms¶

What is the sample variance for numbers from a normal distribution with variance 1?¶

In [30]:

np.random.seed(15)
x_ = np.random.normal(0, 1, int(1e6))
x = 1e12 + x_
var(x)

Out[30]:

-1328166901.4739892

Use functions from numerical libraries where available¶

In [31]:

np.var(x)

Out[31]:

1.001345504504934

There is also a variance function in the standard library, but it is slower for large arrays.

In [32]:

import statistics

statistics.variance(x)

Out[32]:

1.0013464175061981

Note that numpy uses does not use the asymptotically unbiased estimator by default. If you want the unbiased variance, set ddof to 1.

In [33]:

np.var([1,2,3,4], ddof=1)

Out[33]:

1.6666666666666667

In [34]:

statistics.variance([1,2,3,4])

Out[34]:

1.6666666666666667

Useful numerically stable functions¶

Let’s calculate

\[\log(e^{1000} + e^{1000})\]

Using basic algebra, we get the solution \(\log(2) + 1000\).

\begin{align} \log(e^{1000} + e^{1000}) &= \log(e^{0}e^{1000} + e^{0}e^{1000}) \\ &= \log(e^{100}(e^{0} + e^{0})) \\ &= \log(e^{1000}) + \log(e^{0} + e^{0}) \\ &= 1000 + \log(2) \end{align}

logaddexp

In [35]:

x = np.array([1000, 1000])
np.log(np.sum(np.exp(x)))

Out[35]:

inf

In [36]:

np.logaddexp(*x)

Out[36]:

1000.6931471805599

logsumexp

This function generalizes logaddexp to an arbitrary number of addends and is useful in a variety of statistical contexts.

Suppose we need to calculate a probability distribution \(\pi\) parameterized by a vector \(x\)

\[\pi_i = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}\]

Taking logs, we get

\[\log(\pi_i) = x_i - \log{\sum_{j=1}^n e^{x_j}}\]

In [37]:

x = 1e6*np.random.random(100)

In [38]:

np.log(np.sum(np.exp(x)))

Out[38]:

inf

In [39]:

from scipy.special import logsumexp

In [40]:

logsumexp(x)

Out[40]:

984755.5793729819

logp1 and expm1

In [41]:

np.exp(np.log(1 + 1e-6)) - 1

Out[41]:

9.999999999177334e-07

In [42]:

np.expm1(np.log1p(1e-6))

Out[42]:

1e-06

sinc

In [43]:

x = 1

In [44]:

np.sin(x)/x

Out[44]:

0.8414709848078965

In [45]:

np.sinc(x)

Out[45]:

3.8981718325193755e-17

In [46]:

x = np.linspace(0.01, 2*np.pi, 100)

In [47]:

plt.plot(x, np.sinc(x), label='Library function')
plt.plot(x, np.sin(x)/x, label='DIY function')
plt.legend()
pass

notebook/../../build/doctrees/nbsphinx/notebook_S03A_Scalars_Annotated_78_0.png

Scalars¶

Integers¶

Binary representation of integers¶

Bit shifting¶

Overflow¶

Integer division¶

Real numbers¶

Most base 10 real numbers are approximations¶

Never check for equality of floating point numbers¶

Associative law does not necessarily hold¶

Distributive law does not hold¶

Catastrophic cancellation¶

Underflow¶

Prevent underflow by staying in log space¶

Overflow¶

Numerically stable algorithms¶

What is the sample variance for numbers from a normal distribution with variance 1?¶

Use functions from numerical libraries where available¶

Useful numerically stable functions¶

Page contents

Previous page

Next page

This Page