In [1]:
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
In [2]:
import numpy as np
import numpy.linalg as la
Dimension Reduction¶
In [3]:
np.random.seed(123)
np.set_printoptions(3)
Projection when you have an orthogonal basis¶
Note that projection onto a subset of basis vectors for an orthogonal basis just means dropping unwanted directions. The projection matrix is
and
projects onto the space spanned by \(y\)-axis.
PCA from scratch¶
Principal Components Analysis (PCA) basically means to find and rank all the eigenvalues and eigenvectors of a covariance matrix. This is useful because high-dimensional data (with \(p\) features) may have nearly all their variation in a small number of dimensions \(k\), i.e. in the subspace spanned by the eigenvectors of the covariance matrix that have the \(k\) largest eigenvalues. If we project the original data into this subspace, we can have a dimension reduction (from \(p\) to \(k\)) with hopefully little loss of information.
For zero-centered vectors,
and so the covariance matrix for a data set X that has zero mean in each feature vector is just \(XX^T/(n-1)\).
In other words, we can also get the eigendecomposition of the covariance matrix from the positive semi-definite matrix \(XX^T\).
We will take advantage of this when we cover the SVD later in the course.
Note: Here we are using a matrix of row vectors
In [4]:
n = 100
x1, x2, x3 = np.random.normal(0, 10, (3, n))
x4 = x1 + np.random.normal(size=x1.shape)
x5 = (x1 + x2)/2 + np.random.normal(size=x1.shape)
x6 = (x1 + x2 + x3)/3 + np.random.normal(size=x1.shape)
For PCA calculations, each column is an observation¶
In [5]:
xs = np.c_[x1, x2, x3, x4, x5, x6].T
In [6]:
xs[:, :10]
Out[6]:
array([[-10.856, 9.973, 2.83 , -15.063, -5.786, 16.514, -24.267,
-4.289, 12.659, -8.667],
[ 6.421, -19.779, 7.123, 25.983, -0.246, 0.341, 1.795,
-18.62 , 4.261, -16.054],
[ 7.033, -5.981, 22.007, 6.883, -0.063, -2.067, -0.865,
-9.153, -0.952, 2.787],
[-10.091, 9.144, 2.171, -14.452, -5.93 , 17.831, -24.971,
-3.539, 13.002, -8.794],
[ -0.684, -5.433, 4.485, 4.151, -3.025, 9.405, -12.987,
-12.12 , 8.496, -11.511],
[ 1.618, -5.193, 10.388, 6.864, -0.771, 6.267, -8.769,
-11.222, 3.621, -7.55 ]])
Center each observation¶
In [7]:
xc = xs - np.mean(xs, 1)[:, np.newaxis]
In [8]:
xc[:, :10]
Out[8]:
array([[-1.113e+01, 9.702e+00, 2.559e+00, -1.533e+01, -6.057e+00,
1.624e+01, -2.454e+01, -4.560e+00, 1.239e+01, -8.938e+00],
[ 6.616e+00, -1.958e+01, 7.318e+00, 2.618e+01, -5.090e-02,
5.368e-01, 1.991e+00, -1.842e+01, 4.457e+00, -1.586e+01],
[ 7.984e+00, -5.030e+00, 2.296e+01, 7.834e+00, 8.882e-01,
-1.115e+00, 8.609e-02, -8.202e+00, -7.123e-04, 3.738e+00],
[-1.023e+01, 9.007e+00, 2.033e+00, -1.459e+01, -6.068e+00,
1.769e+01, -2.511e+01, -3.676e+00, 1.286e+01, -8.931e+00],
[-7.496e-01, -5.498e+00, 4.419e+00, 4.085e+00, -3.091e+00,
9.339e+00, -1.305e+01, -1.219e+01, 8.431e+00, -1.158e+01],
[ 1.801e+00, -5.009e+00, 1.057e+01, 7.048e+00, -5.873e-01,
6.451e+00, -8.585e+00, -1.104e+01, 3.805e+00, -7.366e+00]])
Covariance¶
Remember the formula for covariance
where \(\text{Cov}(X, X)\) is the sample variance of \(X\).
In [9]:
cov = (xc @ xc.T)/(n-1)
In [10]:
cov
Out[10]:
array([[128.578, -2.133, -6.661, 127.395, 63.27 , 42.369],
[ -2.133, 95.051, 2.269, -1.349, 44.885, 31.637],
[ -6.661, 2.269, 94.934, -5.048, -1.141, 30.275],
[127.395, -1.349, -5.048, 126.993, 63.196, 42.723],
[ 63.27 , 44.885, -1.141, 63.196, 54.408, 36.838],
[ 42.369, 31.637, 30.275, 42.723, 36.838, 36.563]])
Check¶
In [11]:
np.cov(xs)
Out[11]:
array([[128.578, -2.133, -6.661, 127.395, 63.27 , 42.369],
[ -2.133, 95.051, 2.269, -1.349, 44.885, 31.637],
[ -6.661, 2.269, 94.934, -5.048, -1.141, 30.275],
[127.395, -1.349, -5.048, 126.993, 63.196, 42.723],
[ 63.27 , 44.885, -1.141, 63.196, 54.408, 36.838],
[ 42.369, 31.637, 30.275, 42.723, 36.838, 36.563]])
Eigendecomposition¶
In [12]:
e, v = la.eigh(cov)
In [13]:
idx = np.argsort(e)[::-1]
In [14]:
e = e[idx]
v = v[:, idx]
Explain the magnitude of the eigenvalues¶
Note that \(x4, x5, x6\) are linear combinations of \(x1, x2, x3\) with some added noise, and hence the last 3 eigenvalues are small.
In [15]:
plt.stem(e)
pass

The eigenvalues and eigenvectors give a factorization of the covariance matrix¶
In [16]:
v @ np.diag(e) @ v.T
Out[16]:
array([[128.578, -2.133, -6.661, 127.395, 63.27 , 42.369],
[ -2.133, 95.051, 2.269, -1.349, 44.885, 31.637],
[ -6.661, 2.269, 94.934, -5.048, -1.141, 30.275],
[127.395, -1.349, -5.048, 126.993, 63.196, 42.723],
[ 63.27 , 44.885, -1.141, 63.196, 54.408, 36.838],
[ 42.369, 31.637, 30.275, 42.723, 36.838, 36.563]])
Algebra of PCA¶
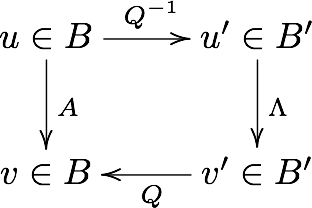
Commuative diagram¶
Note that \(Q^T X\) results in a new data set that is uncorrelated.
In [17]:
m = np.zeros(2)
s = np.array([[1, 0.8], [0.8, 1]])
x = np.random.multivariate_normal(m, s, n).T
In [18]:
x.shape
Out[18]:
(2, 100)
Calculate covariance matrix from centered observations¶
In [19]:
xc = (x - x.mean(1)[:, np.newaxis])
In [20]:
cov = (xc @ xc.T)/(n-1)
In [21]:
cov
Out[21]:
array([[1.014, 0.881],
[0.881, 1.163]])
Find eigendecoposition¶
In [22]:
e, v = la.eigh(cov)
idx = np.argsort(e)[::-1]
e = e[idx]
v = v[:, idx]
In original coordinates¶
In [23]:
plt.scatter(x[0], x[1], alpha=0.5)
for e_, v_ in zip(e, v.T):
plt.plot([0, e_*v_[0]], [0, e_*v_[1]], 'r-', lw=2)
plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.axis('square')
plt.axis([-3,3,-3,3])
pass

After change of basis¶
In [24]:
yc = v.T @ xc
In [25]:
plt.scatter(yc[0,:], yc[1,:], alpha=0.5)
for e_, v_ in zip(e, np.eye(2)):
plt.plot([0, e_*v_[0]], [0, e_*v_[1]], 'r-', lw=2)
plt.xlabel('PC1', fontsize=14)
plt.ylabel('PC2', fontsize=14)
plt.axis('square')
plt.axis([-3,3,-3,3])
pass

Explained variance¶
This is just a consequence of the invariance of the trace under change of basis. Since the original diagnonal entries in the covariance matrix are the variances of the featrues, the sum of the eigenvalues must also be the sum of the orignal varainces. In other words, the cumulateive proportion of the top \(n\) eigenvaluee is the “explained variance” of the first \(n\) principal components.
In [26]:
e/e.sum()
Out[26]:
array([0.906, 0.094])
Note that the PCA from scikit-learn works with feature vectors, not observation vectors¶
In [29]:
z = pca.fit_transform(x.T)
In [30]:
pca.explained_variance_ratio_
Out[30]:
array([0.906, 0.094])
The principal components are identical to our home-brew version, up to a flip in direction of eigenvectors¶
In [31]:
plt.scatter(z[:, 0], z[:, 1], alpha=0.5)
for e_, v_ in zip(e, np.eye(2)):
plt.plot([0, e_*v_[0]], [0, e_*v_[1]], 'r-', lw=2)
plt.xlabel('PC1', fontsize=14)
plt.ylabel('PC2', fontsize=14)
plt.axis('square')
plt.axis([-3,3,-3,3])
pass

In [32]:
plt.subplot(121)
plt.scatter(-z[:, 0], -z[:, 1], alpha=0.5)
for e_, v_ in zip(e, np.eye(2)):
plt.plot([0, e_*v_[0]], [0, e_*v_[1]], 'r-', lw=2)
plt.xlabel('PC1', fontsize=14)
plt.ylabel('PC2', fontsize=14)
plt.axis('square')
plt.axis([-3,3,-3,3])
plt.title('Scikit-learn PCA (flipped)')
plt.subplot(122)
plt.scatter(yc[0,:], yc[1,:], alpha=0.5)
for e_, v_ in zip(e, np.eye(2)):
plt.plot([0, e_*v_[0]], [0, e_*v_[1]], 'r-', lw=2)
plt.xlabel('PC1', fontsize=14)
plt.ylabel('PC2', fontsize=14)
plt.axis('square')
plt.axis([-3,3,-3,3])
plt.title('Homebrew PCA')
plt.tight_layout()
pass

PCA and SVD¶
Geometry of SVD¶
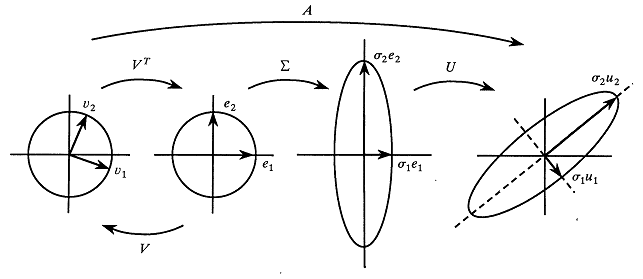
Geometry of SVD¶
If we assume that the columns of a mean centered matrix \(X\) are observations, then PCA (up to a scaling factor) is
\(XX^T = Q \Lambda Q^T\)
With SVD, we have
\(X = U \Sigma V^T\)
and
\(X^T = V \Sigma U^T\)
and hence
\(XX^T = U \Sigma^2 U^T\)
So
\(U\) and \(Q\) are equivalent and \(\Sigma^2 \propto \Lambda\)
In [ ]:

