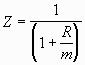
Copyright 1995 by Campbell R. Harvey and Stephen Gray. All rights reserved. No part of this lecture may be reproduced without the permission of the author.
Latest Revision: July 1996.
Consider an annuity of $1 payments, n times per year for m periods at a nominal rate of R.
We could find the present value of each of these individual cash flows. The present value of the first cash flow is simply Z.
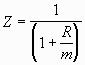
The present value of the second cash flow is the value of $1 discounted back two periods. This is equal to Z2.

In general, the present value of the kth cash flow will be Zk.
If we add all of these cash flows together, we get the value of the annuity:
An = Z + Z2 + Z3+ . . . + Zn
or:
![]()
You may recognize this, from Calculus classes, as a finite geometric series. The formula for the sum of such a series is:
![]()
To prove this, a trick is used. Starting with our original equation:
An = Z + Z2 + Z3+ . . . + Zn
we can multiply both sides of the equation by Z to get another equation:
ZAn = Z2 + Z3 + Z4+ . . . + Zn+1
If we subtract the second equation from the first, several of the terms cancel out. We are left with:
An-ZAn = Z-Zn+1 = Z(1-Zn)
Divide both sides of the equation by (1-Z) and we get:
![]()
If the annuity is a dollars per period rather than $1 per period, we could use the same logic to discover that the value of the annuity is:
![]()