10. “Optimal” Scoring Model

Description:

Utilizing particular quintiles from the single-variable models and a mean-variance optimizer, we were able to determine the “optimal” weights, or scores, for each quintile. Each quintile is essentially a single portfolio, with a related expected return (mean), standard deviation, and covariance with the other quintile portfolios.

We selected six quintile portfolios, and utilized our in-sample data (1988-1998) to generate the “optimal” weights. Our only constraint was that the standard deviation of the monthly returns of the portfolio of quintile portfolios would equal that of the market (S&P 500). The quintile portfolios and related weights (scores) are listed below. Note that the weights (scores) were generated from the mean-variance optimizer, using the equal-weighted quintile portfolio monthly returns as the data set.

Factor	Quintile #	Score
FY1 Yield	1	3.42
FY1 Yield	2	0.64
FY1 Yield	5	-1.20
FY1 Rev Ratio	1	0.04
Div. Yield	1	0.92
LTM EPS Yield	1	-2.83

Utilizing the above weights, or scores, the in-sample time period would have produced a monthly return of 3.74%, with a standard deviation of 3.78%. This represents a monthly excess return of 2.21%.

The real test, however, comes when testing the scoring model for the out of sample time period (1999-2003).

Analysis

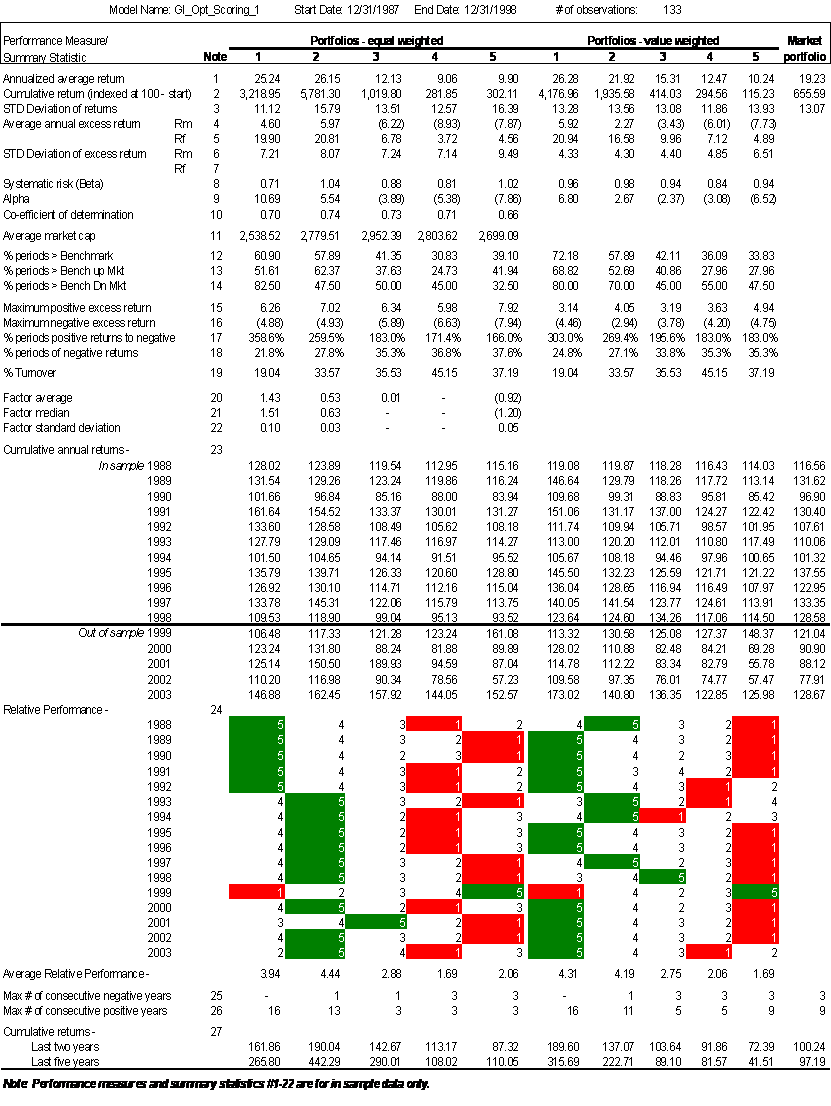
Equal Weighted: Particularly noteworthy is that during the in-sample time period quintiles 1 and 2 have essentially the same annualized average return (25.24% and 26.15% respectively), but quintile 1 has significantly lower volatility (11.1% versus 15.8% respectively). Furthermore, quintile 2 has a turnover ratio more than 1.5 times that of quintile 1.

With regards to relative performance, quintile 1 performs best (i.e., higher return) through 1992, but performs worse than quintile 2 thereafter. A long/short strategy of long quintile 2 and short quintile 5 during would have outperformed the market by a significantly. Note the five-year cumulative return data in the table below.

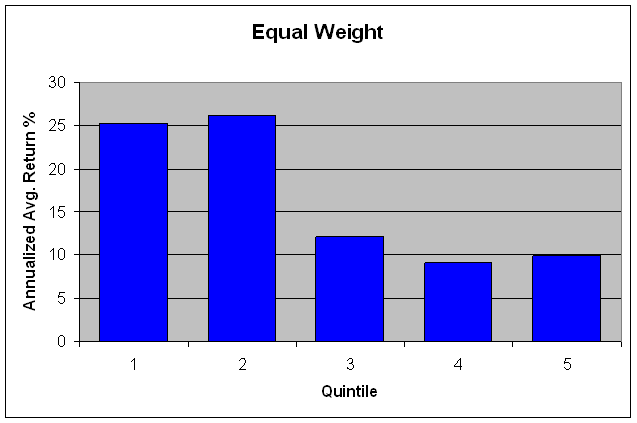
Value Weighted: The value-weighted portfolios offer some interesting data. Quintile 5 has been the worst performer in seven of the past nine years. In 2003 quintile 5 was the second-to-worst performing of the value-weighted portfolios. A long/short strategy (long quintile 1 and short portfolio 5) would have performed very well in the out of sample time period. The strategy would have produced excess returns in all but one of the years. In 1999 the strategy would have returned a loss of 34%, while the market generated a positive return of 21%. The underperformance of this strategy in 1999, however, would have been erased by the large out performance in the subsequent years.

Of some concern is the turnover ratio of quintile 5. Although we have not quantified the trading costs and their effects on returns, a 45% turnover ratio appears high and may minimize the potential for realizing the returns of a long/short strategy.

Conclusion:

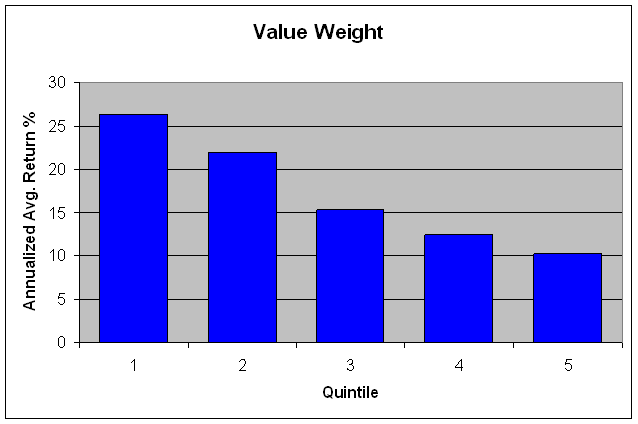
This “optimal” scoring model generates very attractive returns in the out of sample time period. Despite a significant loss in 1999, the loss turns into a significant profit in the subsequent years. These profits in 2000 through 2003 are largely attributable to the ability of the scoring model to identify the “losers” (quintile 5). If one had implemented this strategy in the beginning of 1999, patience and commitment to the model would have been critical in realizing the profits generated in the subsequent time periods. Furthermore, it is possible that trading costs would have severely reduced the returns represented by this model.