
Copyright 1995 by Campbell R. Harvey. All rights reserved. No part of this lecture may be reproduced without the permission of the author.
Latest Revision: October 26, 1995.
The term structure of interest rates or the yield curve is the relation between yields observed today on bonds of different maturity. The yield curve is upward sloping if longer term bonds have higher yields than shorter term bonds or Treasury bills. The curve is flat if all the yields are approximately the same. The structure is inverted if yields on short term bills are higher than long term bonds.
There have been many theories proposed to explain the term structure of interest rates. As the graph below shows, it is quite variable. The three main theories that you probably studied in your macro course are: expectations, liquidity preference and preferred habitat. The expectations theory just says that a positively sloped yield curve means that investors expect rates to go up. Liquidity preference suggests that a rate premium is attached to longer term bonds because they are more volatile. The preferred habitat says that different rates across different maturities are due to differential demand by investors for particular maturities.
There are problems with all of these theories. Consider an alternative story. The yield curve tells us about future economic prospects. If the yield curve is inverted, it is because people are giving up their short term investments and locking in longer term investments to weather a potential recession. This is just hedging. In the good state of the economy, you give up some wealth to hedge against a potential recession. You prefer smooth consumption expenditures to volatile ones. This theory is presented in my thesis paper Harvey (1988, Journal of Financial Economics) [P1] and applied in many other papers such as Harvey (1991, Journal of Fixed Income [P6].
I find that an inverted yield curve has preceeded every recession in the last 25 years. Consider the most recent business cycle (which is an out-of-sample test of my theory). The yield curve inverted in the summer of 1989. The inversion was mild (less than one percent) and lasted three quarters. The official peak of the business cycle was July 1990 and the trough March 1991. The yield curve predicted the timing, duration and magnitude of the recession.
See The Term Structure of Interest Rates.
We have calculated what happens to bond price when there is an interest rate change. Consider the same an example that we previously pursued:
Example
Cash (12% Interest) (13% Interest) (14% Interest) Year Flow Zeros PV Zeros PV Zeros PV
1 12 .893 10.71 .885 10.62 .877 10.53 2 12 .797 9.57 .783 9.40 .769 9.23 3 12 .712 8.54 .693 8.32 .675 8.10 4 12 .636 7.63 .613 7.36 .592 7.10 5 112 .567 63.55 .543 60.82 .519 58.17 Bond Price 100.00 96.52 93.13
As the interest rate goes up, the price of the bond decreases. At a 12% interest rate, the bond is valued exactly at par -- but if the rate increases to 13%, the coupon stream and the final payment of the principal becomes less valuable to the investor and hence the price decreases. The decline is even more severe when the rate jumps to 14%. The holding period return also decreases. If this was a six year bond bought at par and held for one year, then the return on holding the bond is 8.52% if the rates go to 13% and 5.13% if the rates go to 14%. You can imagine that bigger swings in the rates could cause negative holding period returns. In this case, the capital loss exceeds the gain from collecting the coupon. The longer the maturity of the bond the more severe the price changes when the yield changes.
A measure of the volatility of the bond price movement is valuable. We will consider two measures: duration and elasticity. Both of these measures will give us local approximations, i.e., they will be accurate for only small movements in the rates.
First, let's review the formula for bond price.

where B represents the price of the bond. Note that the cash flows can represent coupon payments and principal. The logical way to measure the sensitivity of the bond price to changes in the interest rate is to take the first derivative of B with respect to r. We can write the bond price formula:

If we adjust this measure by dividing by the bond price and multiplying by one plus the market yield, we get a measure of duration first introduced by Macaulay in 1938.

Duration was invented as alternate measure of the timing of the cash flows from bonds. The pitfall in using the maturity of a bond as a measure of timing is that it only takes into consideration the final payment of the principal -- not the coupon payments. Macaulay suggested using the duration as an alternative measure that could account for all of the expected cash flows. Duration is a weighted average term to maturity where the cash flows are in terms of their present value. We can rewrite the above equation in a simpler format:
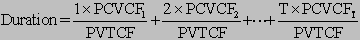
where $PVCF_1$ measures the present value of the cash flow in period one and $PVTCF$ measures the present value of all the cash flows or the bond price.
Now lets consider examples of duration calculations. We will calculate the duration of Bond A and Bond B. The market interest rate is assumed to be 8%. Both bonds have a maturity of 10 years. Bond A has a coupon of 4% and Bond B has a coupon of 8%. Before we calculate the duration measure, we know that Bond B will have a shorter duration. The cash flows from 1--9 years are larger yet the principal is identical. Now lets work it out.
As expected, the bond with the higher coupon rate has a shorter duration. This example illustrates two important properties of duration. First, the duration of a bond is less than its time to maturity (except for zero coupons). Second, the duration of the bond decreases the greater the coupon rate. This can be graphically illustrated:

Notice that the duration and maturity are identical for the zero coupon and the duration decreases with higher coupon rates. This is because more weight (Present Value Weight) is being given to the coupon payments.
The final property is that, as market yields increase, the duration of the bond decreases. This should be intuitively obvious because when we are discounting cash flows a higher discount rate means a lower weight on cash flows in the far future. Hence, the weighing of the cash flows will be more heavily placed on the early cash flows -- decreasing the duration.
The link between duration and volatility is clear because of the first derivative that we used in obtaining the duration formula. There are two alternative measures that are worth investigating. The first is called modified duration. This is derived by dividing the duration measure by one plus the current market yield.

There is also a measure known as elasticity. This is calculated as:

The elasticity measure will be very close in practice to the modified duration measure. The closeness is dependent upon the size of the movement in interest rates. Hence, we see the link between duration, modified duration, and elasticity. Now lets consider another example. We will look at bonds of different maturity. Bond A has a 10 year maturity with a 12% coupon and Bond B has a 5 year maturity with a 12% coupon. Suppose that the market discount rate is 13%.
Rate 10 Year Bond 5 Year Bond Year 13% Cash PV PV/Tot Cash PV PV/Tot
1 .885 12 10.62 .11 12 10.62 .11 2 .783 12 9.40 .10 12 9.40 .10 3 .693 12 8.32 .09 12 8.32 .09 4 .613 12 7.36 .08 12 7.36 .07 5 .543 12 6.52 .07 112 60.82 .63 6 .481 12 5.77 .06 7 .425 12 5.10 .05 8 .376 12 4.51 .05 9 .333 12 4.00 .04 10 .294 112 32.93 .35
94.53 1.00 96.52 1.00
Duration= 6.22 years 4.02 years Modified Duration = 6.22/1.13 = 5.50 4.02/ 1.13 = 3.56 Elasticity=[(100-94.53)/100]/1.00=5.47% [(100-96.52)/100]/1.00=3.48%
Note that the price elasticity measure is very close to the modified duration measure. Note also that the closeness of this measure depends upon the size of the interest rate move. If we go back and calculate the elasticity for our previous example of a bond with a 4% coupon and the relevant discount rate is 8% -- the denominator is now 4% and the approximation will be less accurate.
See Bond price dynamics.
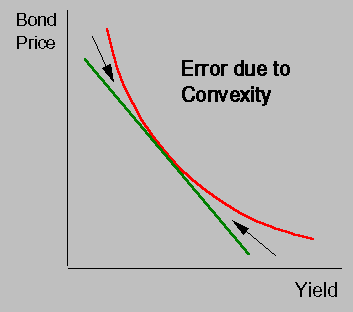
We would like to use the modified duration to approximate bond price movements for a given change in interest rates. The approximation will only be accurate for small changes in the interest rate. For large changes, such as 5%, the approximation deteriorates. This is because the bond price is convex in the yields. We have seen this convexity when we looked at the plot of the bond price against various yields to maturity. Below is a figure that illustrates the error.
Also, if stated interest rates are compounded semi-annually, then the same procedure is used to calculate duration in half years. The duration in half years is converted to years (by dividing by 2) and then transformed into modified duration by divided by the (effective periodic semi-annual rate).
One might wonder why we divide by the semi-annual rate rather than (1) the annual percentage rate or (2) the true annualized rate. The answer, unfortunately, has to do with convention. Most top investment houses calculate the modified duration by dividing by the semi-annual rate - (even if there is quarterly or monthly compounding). In most of my examples, I have annual compounding so I don't have to worry about this convention.
Below is a numerical example using annual rates. Suppose we have two bonds with identical coupon rates of 10%. Bond A has a maturity of 5 years and Bond B has a maturity of 10 years. Let's estimate the error of the duration approximation for price change for a 5% increase in the discount rate. \vfill \eject
Example
Bond A Bond B
Bond Maturity 5 years 10 years Coupon Rate 10% 10% Modified Duration 3.79 6.14 (at par 10%) Predicted Bond Price Move -18.95% -30.72% Actual Bond Price Move -16.76% -25.09% Error of Duration Approx 2.19% 5.63%
The reason for this error is the bond price convexity. In large interest rate moves, this convexity is increasingly important. Convexity is measure of the way the slope of the bond price -- yield curve is changing. Duration gives us a linear approximation. But if the curve is convex this linear approximation may not be very high quality.
To get convexity, expand the bond price formula:
The general formula for a Taylor Series expansion is:

If this is not familiar, you can review your undergraduate calculus text. It should have a section on Taylor series. Take f(x) to be the pricing function for the bond. The price is a function of the yield (x). Consider the change in the yield to be the hvariable. I cut off the approximation after the second term. The first order part, f'(x), is associated with the duration of the bond and the second order part f''(x) with the convexity of the bond. There will also be a residual part because the Taylor series is only an approximation. He provides tables in which he measures how well each of these parts accounts for price changes for bonds of various maturities. Note that the duration measure that he uses is modified duration.
Suppose, for investment purposes, you own $10 million in 8% 30-year Treasuries. The modified duration is 12. The market value is exactly at par, $10 million. However, you believe rates will move up over the next year. If you do nothing and rates move up from 8% to 9%, you stand to lose $1.1 million in market value on your investment. You don't want to sell the bonds - but you would like to protect yourself from this potential loss over the next year. This where we would hedge.
Suppose you plan to buy a house in the next two years. You know that mortgage rates are at 15 year lows and you want to lock in a rate. If you do nothing and rates move up, you will be faced with much more expensive financing. You would like to protect yourself against this potentially higher cost. By hedging, we can lock the mortgage rate in today.
The goal of hedging is to provide a positive cash flow in the bad state. In the first example, our hedge will deliver a payoff that offsets the $1.1 million loss after one year. In the second example, the hedge will deliver a payoff if mortgage rates go up. Even though you finance your mortgage at the higher rate, you are compensated by a positive payoff from the hedge.
We usually use futures or options to execute our hedges. In our first example, there is a 20-year bond
contract trading on the
because the market value of the CBOT contract is $100,000. A=150. Of course, if the rates move
the other way, the gain on what we hold is wiped out by the loss in the futures. We have effectively locked
in the 8% rate.
This is our first example of hedging. In actual practice, investors care about matching convexity (and
sometimes skewness and kurtosis).
My BA453 Tactical Global Asset
Allocation provides an indepth analysis of hedging techniques.
Additional information is available in Value and Risk Management Through Derivatives.
Much of the materials for this lecture are from Douglas Breeden, "Interest Rate Mathematics", Robert
Whaley, "Derivation and Use of Interest Formulas" and Campbell R. Harvey and Guofu Zhou, "The Time
Value of Money".
BA 350
Index Page
Acknowledgement
Campbell Harvey's Home Page