CELLULAR
AUTOMATA |
|
One
dimensional cellular automata

The pigment cells on the growing edge of the tent shell communicate with one another according to noisy one-dimensional two-state cellular automata rules.
|
|
|
A 1-dimensional 2-state Cellular Automaton
A 1d CA is among the simplest
cellular automata. Beginning with a random row of 1s and 0s (yellow and
black), progressively new rows of 1s and 0s are added underneath depending
upon the following general rule. Count the number of living cells (yellow)
in the 3-cell neighborhood in the parent row. If that count is equal to
any of the user-selected values (in the white ComboBoxes) a new cell is
born (yellow) in the child row. Each new generation is shown graphically
below its parent. There are 14 possible birth rules, each yielding a different
pattern, any of which may be selected. Note that some of the triangular
patterns closely mimic those found in nature on so-called "tent"
shells. The resulting patterns are shown on the following webpage.
|
|
|
A 1-dimensional Cellular Automaton
with 3-states
This 1-dimensional cellular
automaton has 3-states, compared to the 2-states in the application above.
I have not exhaustively searched the possible rules, so after a number
of experiments, I settled on 13 which the user can select in the ComboBox.
All the rules, except for one, search a 3-cell neighborhood and parents
give birth to children depending upon the number of individuals in that
neighborhood. Sometimes a random element is added. The exception is the
option called "sex." Dave suggested that in a 3-state CA, two
of the states could be considered members of the opposite sex. In such
a world, a child would be born if, and only if, at least one couple could
be found in the 3-cell neighborhood. I found that 3-cells was not a large
enough neighborhood, so I extended it to 5-cells in this example. There
are hundreds of possible rules. See what others produce interesting patterns.
|
|
|
Dave's 1-dimensional Cellular
Automaton with 3-states
Dave's CA is based upon
pattern matching rather than the total number of occupied neighboring
cells. As a result you are able to create asymmetrical patterns and distinguish
between 101, 110 and 011 whereas in a totalizing CA these would all be
summed to 2. A third state may be randomly generated by entering a 2.
The image at the left is produced by entering the values 11002011.
|
|
|
One Dimensional CA - Midi Sampler
This is a sonified version of the one dimensional,
two state cellular automaton developed earlier. The "world"
is 47 cells across, each cell corresponding to a Midi note. With "Sampling
Interval" set at "1" all "living" cells play
their respective chromatic scale notes. However, the interval can be increased
to play fewer notes. The entire CA is shown. The cells that are sampled
are colored in yellow and black. The cells that are ignored are colored
in light and dark gray. In the image to the left the sampling rate was
increased as the CA ran.
|
|
A two
dimensional cellular automata image processor |

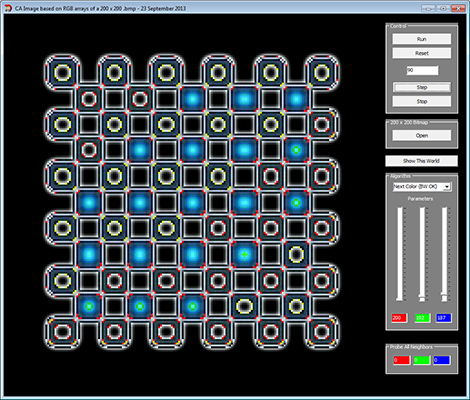
CA Image Version 25 (full-screenCellular Automata Working on 200 x 200 .bmp Images.
Full-screen, autorun version working on a collection of twenty 200x200 bitmaps.
A pop-up menu will enable you to hide the controls.
1 November 2013
|
You may "Open" a single image by using the "Open" button, in which case all controls will work manually.
Pressing the "Auto" button will run the rules up to 250 iterations on each of twenty 200x200 bitmaps which must be in the same folder as the executable. Once the twenty bitmaps have been run, the TrackBars change and the sequence of .bmps is run again. This continues for six different settings of the TrackBar
You may "Open" a single image by using the "Open" button, in which case all controls will work manually.
Pressing the "Auto" button will run the rules up to 250 iterations on each of twenty 200x200 bitmaps which must be in the same folder as the executable. Once the twenty bitmaps have been run, the TrackBars change and the sequence of .bmps is run again. This continues for six different settings of the TrackBars.
|
The following 200 by 200 bitmap (.bmp) images may be imported into the application above or to the right.
Some of the algorithms (rules) will only work on colored images, even if the color is barely discernable.
Some of the images below are true black or white, with RGB values of 0, 0, 0 or 255, 255, 255.
For an image to be colored, one needs only one pixel that does not have equal values of red, green and blue.
The cyan, magenta and yellow checkerboard resulted in the large image of the application on the right.
Note: The images below are .jpg images with links to the .bmp images. Click on an image to see the .bmp target or right-click on an image and "Save Target As" to your dekstop.
 x x  x x  x x  x x   x x  x x  x x  x x 
 x x  x x  x x  x x   x x
 x x x x  x x 
|
Cellular Automata Working on an Image (200 x 200 .bmp)
A proof-of-concept. 22 September 2013.
Based upon Conway's Game of Life, FAST version 23, the world has been expanded to 200 by 200 cells.
Each cell is painted four times its size, in a PaintBox of 800 by 800 squares.
There are three thisWorlds and three nextWorlds, one pair for each of the red, green and blue pixel values.
The red, green and blue dimensions of a pixel each range from 0 (black) to 255 (full saturation).
Several simple algorithms (rules) explore the possibilities...
|
INCREDIBLE - Conway's game of life running on Conway's game of life |
|

OTCA Official Website
LifeWiki: the OTCA MetaPixel |

ZOOM - LIFE ON LIFE
The Game-of-Life programmed to run the Game-of-Life.
Note that the size of the metapixel is 2048x2048. It is thus 2,000 times larger than a pixel and occupies 4 million times as many cells. A single iteration of a metapixel will probably take about 10,000 iterations. The smallest GOL creatures require at least a 5 x 5 pixel world. Thus the smallest meta GOL creatures would require about a 10,000 x 10,000 pixel world. |
Alan Hensel's "Digital Counter" running on Conway's Game of Life:
Alan Hensel's "counter" resembles a Jacquard loom or a computer that "prints" decimal digits
from data stored on four "tapes."
Each "tape" consists of a loop of diagonal "gliders" which is threaded around four "pulleys" or reflected from four "mirrors."
Four "copiers" at the top make duplicate "gliders" and send them to a central "printer" which creates an upward stream of "creatures" appearing as dots of a 4x5 dot-matrix numerals. |
|
Game of Life "Digital Counter" by Alan Hensel 1994
Modifications by Nick Gessler 13 February 2013
Black cells are alive. Brown and white cells are dead. "Repaint" renders all dead cells brown. Newly dead cells are rendered white. As a result, the user can distinguish active from inactive areas. Given enough space, the numerals will
be generated forever. To save space in this version, the numerals
wrap around the bottom and are destroyed when they hit
the red bar. The red bar simply deletes all living cells that touch it.
Four "tapes" provide data for the counter. More may be added. The tapes may be lengthened and their data modified. Right-click to zoom in. Left-click to zoom out.
Two accelerations have been added:
1) Renderings are made to a TBitmap and the TBitmap is drawn to the PaintBox at each iteration.
2) After 1000 iterations the unused space (the brown cells) are not interrogated.
Executable
Unit1
Source Code
Unit2
Source Code
Project
Files Zipped
Data
File "GOL counter data.txt" Right-click and "Save As." |
Just Conway's Game of Life
A 2-state, 2-dimensional cellular automata.
In a cellular (gride-like) world, every cell is either dead (red) or alive (green).
At every iteration, each cell is asked what it will be in the next iteration, but no one gets to change until they all do, simultaneously.
If a cell is dead and has exactly three (3) living neighbors, it will become alive. Otherwise it will stay dead.
If a cell is alive and has either two (2) or (3) living neighbors, it will stay alive. Otherwise it will die. |
Two Dimensional
Cellular Automata including Conway's
Game of Life
Paul Callahan's Website:
|
Mirek Wojtowicz's Website:
|
|

A rare large oscillator:
|
What is the species diversity of Conway's world? For example what is the percentage of creatures of each type resulting from a 50% random initial setting. Here's a start...
hotdog 65% +
bar 20% +
widefish 8% +
box 4% +
longfish 2% =
TOTAL 100%
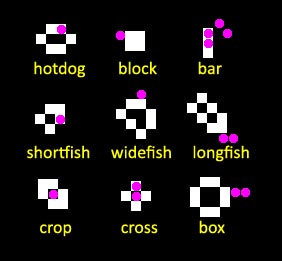
What are the creature's responses to environmental factors? For example, here are nine creatures showing their "kill spots" in magenta (places where a living cell will make them dissapear. Other spots may transform them into yet more configurations. |
SLOW Conway's Game of Life - Version 23 - 19 September 2012
Drawing directly to the PaintBox.
This version makes all its calls to the graphics card and the display using PaintBox->Canvas. It makes hundreds or thousands of calls each iteration, slowing down the application when the world is crowded.
This is a basic, stripped-down and straight-forward application which can be written in one or two sessions.
It is a good place to begin.
It has been written as a coordinated system of relatively short functions, commented and neatly formatted.
An independent function enables wrap-arounds in the toroidal world.
|
FAST Conway's Game of Life - Version 23 - 19 September 2012
Drawing directly to a TBitmap.
This version makes most of its calls to TBitmap->Canvas and only calls the PaintBox->Canvas once per iteration using: Form1->PaintBox1->Canvas->Draw(0, 0, worldBMP). The speed-up is particularly noticeable when the world is crowded.
This is a basic, stripped-down and straight-forward application which can be written in one or two sessions.
It is a good place to begin.
It has been written as a coordinated system of relatively short functions, commented and neatly formatted. An independent function enables wrap-arounds in the toroidal world.
|
|
Conway's Game of Life - Three Worlds in Parallel - September 2011
In our own world beginning with the Big Bang, evolution has created an infinite variety of complex forms.
If cellular automata in some ways mimic that bottom-up process of emergence,
Is there any way to breathe evolution into Conway's world?
How can we add complexity to its behavior while keeping its physics relatively simple?
In this version, three GOL worlds (red, green, blue) run independently on top of one another.
The rendering combines the three additive primary colors into a fourth world represented on the screen with the additional colors of cyan, magenta and yellow. Can this fourth world on the screen be further modified to produce yet more complex behavior?
|
|
Game Of Life & High Life - Version 22b: AUTORUN & FULLSCREEN
22 September 2013
Right-Click on the screen for a PopUp Menu which allows you to hide or restore the controls.
This version has been modified to run automatically as a full screen display. It should run 24/7 on any size display.
A single timer manages the reset(), run() and placeCreature() functions.
The timer interval is reset depending on the random distribution of the creatures introduced.
Resizing the display to full screen is explained in the beginning of the source code.
Horizontal, vertical and crossed line patterns have been added.
Based upon the following speed test, the FAST version runs at three times the rate of the SLOW version.
The test: Set the tail length to maximum. Kill the world and place a space-filler on the world. Run for 30 seconds and record the number of iterations computed and displayed. .
Slow Version 22
All rendering to TPaintBox. |
3 x Faster Version 22b
All rendering to a TBitmap during each iteration.
TBitmap drawn to TPaintBox only once per iteration. |
|
|
|
|
Conway's Game of Life - Version 21 - CREATURES, FADERS & HILIFE - 2009
Derived from the version directly below, this version includs all the features below pluse several enhancements:
A "makeValid" (mv()) function has been added to insure that array indices wrap around the world with no problems.
Consequently creatures may be added anywhere and they will be automatically wrapped around the world.
"High Life" rules have been implemented allowing a person to run the only known replicator in the Game of Life.
|
|
Conway's Game of Life - Version 20 - CREATURES & FADERS - 2009
Derived from the version directly below, this version allows many of the creatures on Paul Callahan's Website to be placed in the world with a right-click of the mouse. Paul's patterns, coded as periods and asterisks "...**..*", can be easily pasted into new creature array declarations and definitions and changed to 1s and 0s with trailing commas "0,0,0,1,1,0,0,1," in Borlans's own source code editor. Code has been added to prevent creatures from being added outside the world array. The "current world" is the world that is currently displayed. The "beginning world" was the world at iteration zero "0" just before "Run" was pressed.
|
|
Conway's Game of Life - Version 19 - FADERS - 2009
Derived from the version directly below, this application shows the living cells as WHITE but allows the dead cells to decay with colors ranging from HOT to COLD. . As far as the rules go, there are no changes, recently dead and long dead are considered "dead" for the count of living neighbors. But for the graphic visualization, the recently dead cells decay from white through magenta and down to blue and black. The visualization makes the recent "history" of the simulation more apparent. A TrackBar is included to vary the "tail length" of the decay, ranging from 0 to 100 but defaulting to 50. More
creatures are here: Conway's
GOL Glossary:
|
|
|
Conway's Game of Life - 2008
With memory, save and open functionality.
Derived from the "Short
Version" directly below, this version remembers every starting configuration
after a reset or after a file has been opened. The remembered configuration
may be recalled and/or saved. A left-click will change the status of a
single cell on the PaintBox.
If one of the two creatures are selected (the background will turn yellow)
a right-click will then place that corresponding creature on the PaintBox.
The images consist of an TImage
object with a transparent bitmap as their Picture
properties. Each TImage
is placed on top of a TPanel
whose color is changed to to indicate which creature was chosen. More
creatures are here: Conway's
GOL Glossary:
|
|
Conway's Game of Life - Immortality Tweak - 10 February 2010
A tweak of the Spring 2010 version built in class. What can be done to Conway's Game of Life to promote more emergences? The only way to push the GOL towards more complexity is to enrich the rules, the environment, or both. The creatures (objects) that emerge from the GOL are so fragile that a simple glider can destroy them. Is there a way to insure longevity? In this experiment, cells that live for more than a certain number of iterations become immortal. Immortal cells are colored clGreen instead of clLime. For experiments, the number of iterations for a run may be selected as can the age of immortality. A MouseOver will probe any cell for its current age. From a random beginning, maze-like patterns slowly grow. From a simple glider, a number of patterns emerge with immortalities of 1, 2, 3 and 4 (see illustrations).
Paul Callahan's Conway's
GOL Glossary: |
|
Conway's Game of Life - Spring - 2010
As far as we got building the GOL together during this semester.
A "makeValid" (mv()) function has been added to insure that array indices wrap around the world with no problems.
Consequently creatures may be added anywhere and they will be automatically wrapped around the world.
Creatures may be cut and pasted into creature array declarations and definitions from Paul's GOL Glossary and converted into valid code using Borland's source code editor.
Rendering has been speeded up using a showChanges function.
Computing may be slowed using the trackbar.
Paul Callahan's Conway's
GOL Glossary: |
|
Conway's Game of Life - Short
Version
A relatively efficient
coding of Conway's Game of Life. It is fast and lets the user build shapes
by clicking on the screen. It could easily be improved, but I will leave
that to you...
Conway's
GOL Glossary: |
|
|
Conway's Game of Life - Deaths
Colored
The world grid has been
changed from a Boolean to an Integer array so that the iteration (deathday)
on which a cell dies is captured and painted as a color gradient. The
display will repaint itself. Just for fun, when the simulation is reset,
it shakes, as if to rid itself of unwanted lifeforms. The Re-Color button
sets the range for coloring to the current iterations. For birthdays instead
of deathdays, see below:
|
|
|
Conway's GOL - Transparent &
Births Colored
Instead of rendering on
a PaintBox, we render on an Image component. We create to TImages: ImageBackground
and ImageGOL. Both are transparent, the same size and lay on top of one
another. Both contain an extra line of pixels at the bottom. In ImageBackground
that line is clRed. The ->Picture property of ImageGOL is copied from
the ->Picture property of ImageBackground when the Form is created.
When we render "dead" cells to ImageGOL->Canvas we do so
in the transparent color clRed. It would be better to choose a transparent
color that is NOT on the edges of the color cube... Also set:
Form1->DoubleBuffered
= true;
|
|
|
Conway's Game of Life - Births
Colored
The world grid has been
changed from a Boolean to an Integer array so that the iteration (birthday)
on which a cell is born is captured and painted as a color gradient. The
display will repaint itself. Just for fun, when the simulation is reset,
it shakes, as if to rid itself of unwanted lifeforms. The Re-Color button
sets the range for coloring to the current iterations. For deathdays instead
of birthdays, see above:
|
|
|
Visualization and Creature Sampler
A simplified example of
how to enlarge the visualization of an array from single pixels to larger
shapes (rectangles, ellipses and text). Also includes an example of how
to reduce the pixel X and Y values of a mouse-down event to
array indeces. Finally it shows how you can introduce "creatures"
(patterns) to the array and visualize them. Conway's rules are NOT
encoded which is why there is no RUN button.
|
|
|
Simone's "Life"
A variation on Conway's "Game of Life" which
includes the ability to "add a creature" to the simulation during
a run.
Executable |
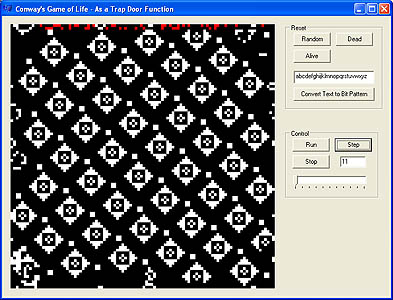
These text strings will produce
some interesting patterns:
"abcdefghijklmnopqrstuvwxyz" (step 11), "U", "*",
"U*", "ab", "p", "submit", "d"
ends with a large 3-cycle oscillator.
Metaphorical madness: try "oscillator",
"Oscillators", "hotdog", "georgebush",
"iraq", "iran", and "usa". Are there hidden
messages here? (Just kidding...)
|
Conway's Game of Life - Trap Door
How can you recognize a password as valid without
keeping a file of valid passwords on hand, which someone might steal?
One answer is a "trap-door" or "one-way" function,
which converts the password into a unique pattern. You can then keep that
file of patterns on hand, and even if it is stolen, the passwords will
be safe. The reason is this: while it is relatively easy to go from the
password to the pattern, it is nearly impossible to reconstruct the password
from the pattern. Here we have applied that idea to Conway's Game of Life.
Enter any text (the password) and the software will convert it to a string
of bits (displayed in color), and then repeat that string to fill the
world (in black-and-white). We run the world through a fixed number of
frames, and take the resulting pattern as validation for the password.
We keep a file of resulting patterns on hand; we don't keep the password
around to be stolen. There
are 210,000 or 1.99 x 103010 different starting
patterns.
|
|
|
Conway's Game of Life - GOL Multiruns Version B - September 2013
Detecting a stable world and counting creatures
This begs the question, "What does it mean to be 'stable?'" In this version, we make the tentative simplifying assumption that the world is "stable" when its population remains unchanged. We monitor the population as the
game progresses. with a choice of one of three displays. The population
vs. iteration display plots in black unless the population remains the
same, at which time it ticks the plot in color, the color representing the number of frames of the world which have remained at the same population level. When the population repeats
six times, the ticks turn white and the simulation slows. The new population
vs. old population display produces a scatter plot. The new change in
population vs. old change in population display also produces a scatterplot.
Data points and cells in the game are colored along a spectrum representing
the iteration at which that item was rendered. Some runs end with oscillators,
so they do not terminate in white. Here
are some screen shots of unusual runs.
|
Hexagonal Cellular Automata |
|
XE6 CA Hexagonal - Preliminary Considerations
It is relatively easy to use a 2d square array to represent an hexagonal grid. The array should have an even number of rows and columns. Imagine that every other row is shifted to the right one-half of a cell width, and instead of drawing squares, draw circles (ellipses). The 6-cell neighborhood can be calculated quite easily once one understands the relationship between the shifted rows and the original square grid. This application is a preliminary experiment in writing an algorithm to display the hexagonal cells, respond to mouseDowns properly, and find the 6-cell neighbors of a given cell. It contains no code for CA rules...
The "Show Rectangle" button displays the square grid. Clicking on any square displays the square and hexagonal coordinates but changes the display to the hexagonal grid.
The "Show Circle" button displays the shifted hexagonal grid. A shifted mouseDown on any circle displays its column (x) and row (y) coordinates and also colors its neighbors gray. The algorithm incorporates wrap around.
|
Other
Two-Dimensional Cellular Automata |
|
|
A Generalized 2d 2-state CA
By default, Conway's "Game
of Life" rules are checked, but you may change the rules at any time,
even during a run.
There are 2^9 possible rules governing a dead cell and another 2^9 possible rules governing a living cell.
In short, there are 2^18 (or 262,144) possible different rules. Not all of them are interesting...
- A dead cell will be BORN if it
has (the checked) living neighbors. Otherwise it will stay dead.
- A live cell will stay LIVE if
it has (the checked) living neighbors. Otherwise it will die.
You can click on a cell to change its state. Clearing the screen sets all cells to BLACK. Subsequent live cells are colored RED and dead cells are colored GREEN. In the image to the left the BLACK cells are those that have neither been born nor have died. In other words, BLACK cells represent cells dead and unchanged since the last RESET.
|
|
Dave Niebuhr's Implementation of Langton's Ant
Version
3
|
|
|
Garret's Langton's Loops
Self-reproducing cellular automata originated by Chris
Langton. This
version will not work without Borland installed!
|
|
|
A CA with Pattern Matching
A pattern matching rule
set has been implemented and the window has been designed to shake when
cleared. The particular rule set which has been begun is "Sand"
but it has not been finished. I will leave that to you...
|
|
|
Dave's Color Chase
Cells are filled with
a random selection of colors with the three sliders. Dark colors are disallowed
because of poor visibility. Colors tend to migrate towards like colors.
This is a variation on the class of segragation problems.
|
|
|
Planet Wator - A Cellular Automata
Implementation
A simulation of a simulation.
Sharks feed on smaller fish in this virtual ecosystem. Each cell has three
states: shark, minnow and empty ocean. Each cell state is a function of
its neighboring cells. Gestation and stomach size have not been implemented.
Inspired by alife.fusebox.com Planet
Wator simulation. |
|
|
Dave's Improved Planet Wator
A simulation of a simulation.
Sharks feed on smaller fish in this virtual ecosystem.
Inspired by alife.fusebox.com Planet
Wator simulation. |
Three
-Dimensional Cellular Automata |
|
|
Dan's 3d Cellular Automaton
Written in Microsoft Visual
C++.
|
|
Probably
Destined for the Trash Heap |
| |
|
