| |
SUDOKU: How to create a
seemingly random yet valid beginning board:
Go through the following shuffling procedures and then erase any number of cells... |
(Note that starting with a random set of cells in 1 is equivalent switching
any numbers in 4.)
There would appear to be 9! x (3! x 3! x 3!) x (3!
x 3! x 3!) = 16,930,529,280 different valid boards. |

1. Copy an orderd set downwards by shifting the cells one to the right
and to the right by shifting the cells one down. |
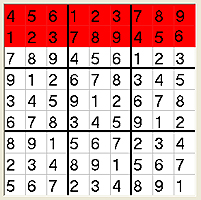
2. You can switch any row with any other as long as they are in the same
square of rows. You can do this as often as you like. |

3. You can switch any column with any other as long as they are in the same
square of columns.xYou
can do this as often as you like. |
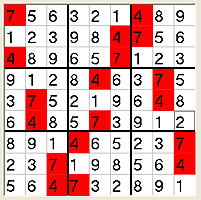
4. You can switch any number with any other anywhere on the board. You can
do this as often as you like. |
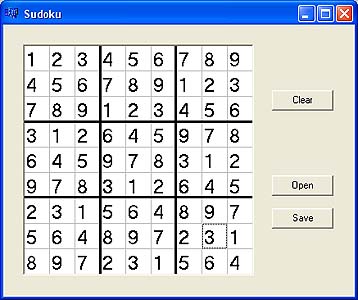
A Sudoku Shell
This application uses the TStringGrid component over
which lines are redrawn to divide the board into nine blocks. It allows
only single digit entries and will flash red and erase a digit which
is duplicated in a column, row or block.
|
Is an exhaustive search practical?
There are 1.97 x 1077
(981) ways to fill the Sudoku board. Only a fraction of these
boards are valid. At 1 billion tries per second it would take 1.38 x 1051
times the age of the Earth to run through all the possibilities. However,
we might get lucky...
There are 362,880 (9!) ways to validly
fill a block. Consequently there are 1.09 x 1050 (9!9)
possible combinations of valid blocks. More of these boards will be valid.
At the same solution rate it would take 7.68 x 1023 times the
age of the Earth to run through all the possibilities. This is an improvement...
Is
an evolutionary search practical?
Evolution procedes through
hill-climbing. Is a board that contains a 5 invalid cells closer to a
valid solution than one that contains 10? If so, then evolution might
work. But it might be the case that a board with 5 invalid cells is along
the path to a dead end and is further from a valid solution than one that
contains 10. Then evolution might well fail. For comparison, a good cryptographic
key exhibits no signs of closeness. Either you have the correct solution
or you don't. There is no hill-climbing, no hint that you are on the right
path.
You may download and
open the configuration you see above:
sudoku-permutations.txt |
|
|
Minesweeper
The classic game playable at three levels. The functionality
is the same as the Microsoft version except that the timer and mines remaining
counts have not been implemented. Unlike the image at the left, the Window
is the size of the "expert" board.
|
|
|
UCLA - opoly
A local variation of the popular board game Monopoly.
This simulation determines one measure of the "value" of game
squares on the board by the number of times each is landed upoon. The
present implementation simulates rolling two dice and the forced moves
resulting from landing on "Go Home" and drawing certain "Contingency"
and "Campus Mail" cards. The cost and rental amount of each
square could be added to the simulation to give a better approximation
of "value."
|
|
|
Snake with Head
In this version, four bitmap images have been imported
representing the four different directions in which the head may be pointing.
A tail and body details could be added in the same manner. There
are some complications regarding the Focus of objects.
|
|
|
Snake with Arrow Keys
A modification of the popular game available on cell
phones. You must guide the snake to eat blue food squares and avoid magenta
poison squares. The snake grows one segment for each blue food square
it eats. It will die if it eats a magenta poison square or if it crosses
itself. The object is to grow the snake as long as possible. You can guide
the snake either by using the arrow keys. The internal representation
in the program consists of a 25-by-25 cell world array and the position
of each segment of the snake in a snake array. There are some complications
regarding the Focus of objects.
|
|
|
Chess
This is an unfinished application with only the visual
representation of the graphics
user interface (GUI) in place. There is no internal representation of
the chess pieces or the chess board at the present time. Two arrays need
to be built, one for the current world [8][8] and one for the next world
[8][8]. Then the pieces need to be represented as coded integers in those
array. I would be pleased if someone would then code the possible moves
of a given piece, marking them with the magenta square. I would be extremely
pleased if all the possible moves of one side could then be evaluated
by the territory under their control. I would be elated if then one side
would automatically move and capture simply to maximize its territory,
the user playing the other side. Note: The EditBoxes need to be disabled
in order for the FormKeyPress event-handler to work.
|
|
|
Chess 2
Some enhancements have been added although
not all the routines worked out by Chris have been implemented. Pieces
can now be moved by clicking to pick them up and clicking again to drop
them. Two end games have been set up.
|
|
|
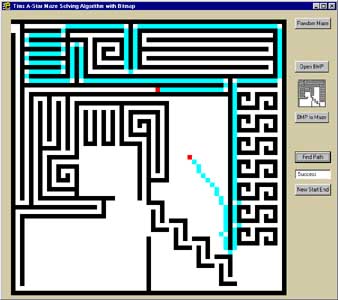
Tim's A* Maze Solving Algorithm
The "A-Star" search algorithm finds the
shortest path between source and target cells (red) in a maze. The path
is traced in cyan, if a path is possible at all.
To do:
- Selected beginning and end points
- Construction and demolition of
walls
- Display of several paths
|
|
|
Tim's A* Maze with Bitmap
Instead of creating random mazes, this version allows
you to import a 61 by 61 cell bitmap image drawn in black-and-white. Two
such images are included. Pictorial images may be reduced in PhotoShop
for different effects.
Two bitmaps:
|
|
Throw Dice by Christina Robinette
A solution utilizing two functions,
one to roll the dice and another to display the result. The display function
is a bit verbose, but it works and adds a novel user prompt.
|
|
Throw Dice by Kathryn Papadopoulos
A straightforward solution that met
all the requirements: function call, icon, title and correct operation
with some elaboration of the fonts.
|
|
Throw Dice by Jack Rosner
One of the more elaborate solutions
to the in-class exam which asked participants to write an application
that rolled two dice, displayed the sum of their faces, and also displayed
the text "Box-Cars" and "Snake-Eyes" if they rolled
a 12 or a 2 respectively. Jack also created a frequency graph to display
the results of numerous throws. Notice that a throw of 7 is the most frequent
(there are many ways to get a 7) whereas throws of 2 and 12 are relatively
rare (there is only one way to get each of these). The call of the random() function is verbose, but it works.
|
|
Multistage Game Logic (a foundation)
This is a model of the program logic which can be used to create a multi-level or multi-stage game. Essentially, a new game is introduced at each stage, and to progress from one stage to another we enlist an event to create a password which will release us from one point in the program and take us to the next.
A work in process... |
Embarcadero C++ Builder - Assorted Games