




Cryptology
Visit our simulations on cryptology
for more information.
SOME AUTHORITATIVE REFERENCES:
SOME WEB RESOURCES:
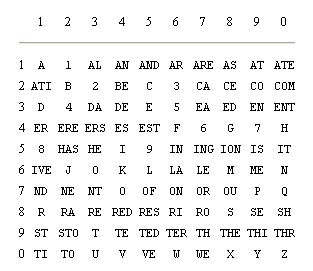
REPRESENTING TEXT
All of these methods are probably still in use today
ABSOLUTE SECURITY with a TRULY RANDOM KEY
One-Time-Systems (Pads, Silk, Tape or Disk) The
Vernam Cipher
A system in which a different scrambled alphabet is used for each character in a message. The set of references to the scrambled alphabets used in a message is referred to as its key and is supplied to the sender and recipient on pads of paper, silk, tape or disk. Typically, the cleartext is added to the keytext to produce a cryptotext. If one knows the key to the ciphertext the cleartext may be recovered by subtracting the keytext from the cryptotext. (All addition and subtraction is done modulo 26; the alphabet wraps around.) The key could be the text from a page of a widely published novel, lead article in an international newspaper or the headline story on cnn.com. This method is unbreakable if, and only if:
The problem with the one-time-pad is that both the sender and recipient have to have copies of a number of keys. The keys must be delivered by courier and every precaution must be made to insure that the keys are not intercepted and copied.
Some One-Time-Systems:
|
Second World War
|
Second World War
|
East German
|
Russian
|
Russian
|
 |
 |
 |
 |
 |
|
A Windows application
for PCs.
|
A numeric representation
of text.
|
|||
 |
||||
PRETTY GOOD SECURITY with a PSEUDO-RANDOM
KEY
Early Beginnings
Below is illustrated one excessively complex device for generating pseudo-random keys by hand. From a few initial settings it was possible to generate a long string of seemingly random numbers. The device was too complicated for use in the field and tended to fall apart if not assembled on a desk. It was abandoned soon after it was introduced to the West German Army during the cold war.
Most of the cipher equipment developed during the Second World War and the Cold War relied on mechanical and electromechanical methods of generating a long pseudo-random number key from a much shorter list of settings. These were mechanical and electromechanical dedicated computers, precursors of today's silicon based machines. The settings, which could change by the hour, the day, the week or month, would be distributed to the sender and receiver long before they were needed. Once the settings were input into the machine, the machine would generate a long key which was otherwise extremely difficult to predict by an outside party. Perusing the various Web links listed above will show you examples of many such devices, the best known being the German Enigma machine.
Another way to look at pretty good security is to say it's not secure enough. If it's not totally secure, then the codes (the ciphers) can be cracked. And so the cryptanalysts set out to search for solutions using guesses (cribs) and advanced statistical methods, frequently aided by cryptographer's mistakes. Inspired by the work of the Poles in early successes in breaking the German Enigma codes, the British and the Americans built huge electromechanical devices dedicated to narrowing the search for plaintexts. These were early computers, programmed in hardware to solve a narrow range of critically important problems. It was during this period of intense research and development that Alan Turing, and others, devised the general architecture of the modern computer.
SOME EXCELLENT VIDEO RESOURCES ON CRACKING
THE ENIGMA
Kept secret for half a century.