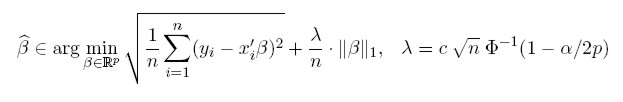The following code files (usually in C++ or MATLAB) have been developed during the past few years as a by-product of research.

• The code used in the "L1-Penalized Quantile Regression in High-Dimensional Sparse Models", with Victor Chernozhukov: R code for Monte Carlo, simple MatLab implementation that requires SDPT3.
  
  
• The code used in "High-Dimensional Sparse Econometric Models, an Introduction", with Victor Chernozhukov:Matlab Code.
  
  
• The code used in the Supplementary Material of "Least Squares After Model Selection in High-dimensional Sparse Models," with Victor Chernozhukov: files (simulation for known standard deviation of the noise)
  
  
• The code used in "Linear and Conic Programming Approaches to High-Dimensional Errors-in-variables Models," with M. Rosenbaum and A. Tsybakov: files (simulation for known standard deviation of the noise)
  
  
• Square-root LASSO is a variant of LASSO that does not rely on estimates of the standard deviation of the noise:
  
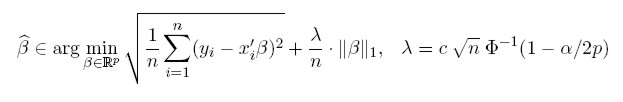
  Available MATLAB code:
  • coordinatewise method (file)
    
  • interior point methods calling SDPT3 (file)
    
  • first order methods calling TFOCS package:
    opts = tfocs_SCD;
    [ beta, out ] = tfocs_SCD( prox_l1(lambda/n), { X, -Y }, proj_l2(1/sqrt(n)), 1e-6 );
    
  • recommended choice of penalty level lambda:
    c = 1.1; ALPHA = 0.05;
    lambda = c*sqrt(n)*norminv(1 - ( ALPHA/(2*p) ), 0,1);
    
  • for other choices of penalty level and discussions click here.
  
  
• Behrens-Fisher Problem: Given two independent random samples {X_i : i=1,...,N_1} and {Y_i: i=1,...,N_2} test whether their respective means coincide in the case where their covariances are unknown and potentially different. We consider the Gaussian case.
  The Gaussian Maximum Likelihood Behrens–Fisher problem is given by the following non-convex problem:
  
  
  
  Available MATLAB code:
  • cutting line method (two versions, with and without the use of a spectral decomposition, files)
    
  • Newton method combined with non-convex line search (file)
    
  • Iterative method (file)
    
  • The cutting line method is guaranteed to converge to a global solution while the iterative method can converge to a local solution.
  
  
• Efficient Projection onto a Second Order Cone:
  
  Available MATLAB code:
  • specialized efficient projection (files)
    
  • interior point method based on SeDuMi (file)
    
  
  

My CV is here