Solving Optimization Problems Computationally¶
In [1]:
%matplotlib inline
%load_ext rpy2.ipython
import os
import glob
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('notebook', font_scale=1.5)
In [2]:
import scipy.linalg as la
import scipy.optimize as opt
1. Curve fitting¶
Actual data from an ELISA experiment. The first column is log concentration, the second is the measured value from the ELISA assay at that concentration. Our task is to fit a 4 parameter logistic function to the observed data.
The 4 parameter logistic has the following form
where \(A\), \(B\), \(C\) and \(D\) are parameters to be determined.
Inspect data¶
In [3]:
data = np.array(
[[ 1. , 3.802],
[ 2. , 3.802],
[ 3. , 3.778],
[ 4. , 3.718],
[ 5. , 3.696],
[ 6. , 3.181],
[ 7. , 1.731],
[ 8. , 0.744],
[ 9. , 0.29 ],
[10. , 0.124],
[11. , 0.064],
[12. , 0.05 ]]
)
In [4]:
x = data[:, 0]
y = data[:, 1]
In [5]:
plt.scatter(x, y, c='red')
pass

Define 4 parameter logistic¶
In [6]:
def f(x, A, B, C, D):
return (A - D)/(1 + (x/C)**B) + D
Find reasonable values for initial parameters¶
In [7]:
A0 = y.max()
D0 = y.min()
C0 = x.mean()
B0 = 1
p0 = [A0, B0, C0, D0]
Using minimize with conjugate-gradient¶
Define the loss function¶
In [8]:
def loss(p, y, x):
A, B, C, D = p
return np.sum((y - f(x, A, B, C, D))**2)
Minimize¶
In [9]:
r = opt.minimize(loss, p0, args=(y, x), method='CG')
In [10]:
r.x
Out[10]:
array([ 3.78699634, 10.87666589, 6.91225087, 0.06131771])
Plot the fit¶
In [11]:
xp = np.linspace(x.min(), x.max(), 100)
plt.plot(xp, f(xp, *r.x))
plt.scatter(x, y, c='red')
pass

Using nonlinear least squares¶
Define least squares residues¶
In [12]:
def res(p, y, x):
A, B, C, D = p
return (y - f(x, A, B, C, D))**2
Minimize¶
In [13]:
r = opt.least_squares(res, p0, args=(y, x))
In [14]:
r.x
Out[14]:
array([ 3.7756568 , 11.02097427, 6.90573049, 0.07695251])
Plot¶
In [15]:
xp = np.linspace(x.min(), x.max(), 100)
plt.plot(xp, f(xp, *r.x))
plt.scatter(x, y, c='red')
pass

Using curve_fit¶
This is the most convenient as you can work with the function directly. It uses the Levenberg-Marquadt algorithm.
Minimize¶
In [16]:
p, pcov = opt.curve_fit(f, x, y, p0)
In [17]:
p
Out[17]:
array([ 3.78699349, 10.87690577, 6.91224723, 0.06132645])
Plot¶
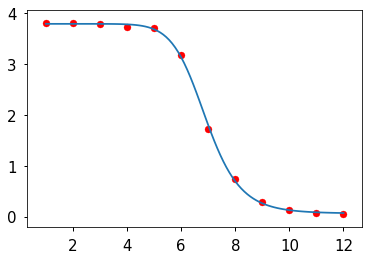
In [18]:
xp = np.linspace(x.min(), x.max(), 100)
plt.plot(xp, f(xp, *p))
plt.scatter(x, y, c='red')
pass
2. Constrained optimization¶
A. Using scipy.optimize, find the values of \(x\) and
\(y\) that minimize \(e^{x^2 + y^2}\) in the unconstrained case
and in the presence of the constraint that \(x + y = 3\). Use (1,1)
as a starting guess.
In [19]:
opt.minimize(lambda x: np.exp(x[0]**2 + x[1]**2),
np.ones(2))
Out[19]:
fun: 1.0000000000000002
hess_inv: array([[ 0.74999784, -0.25000216],
[-0.25000216, 0.74999784]])
jac: array([0., 0.])
message: 'Optimization terminated successfully.'
nfev: 32
nit: 7
njev: 8
status: 0
success: True
x: array([-8.0369005e-09, -8.0369005e-09])
In [20]:
opt.minimize(lambda x: np.exp(x[0]**2 + x[1]**2),
np.ones(2),
constraints=dict(type='eq', fun=lambda x: x[0] + x[1] - 3))
Out[20]:
fun: 90.01713130056051
jac: array([270.05131435, 270.05148602])
message: 'Optimization terminated successfully.'
nfev: 44
nit: 9
njev: 9
status: 0
success: True
x: array([1.49999954, 1.50000046])
B. A milkmaid is at point A and needs to get to point B. However, she also needs to fill a pail of water from the river en route from A to B. The equation of the river’s path is shown in the figure below. What is the minimum distance she has to travel to do this?

Milkmaid problem
In [21]:
def f(x, A, B):
return la.norm(x-A) + la.norm(x-B)
In [22]:
def g(x):
return x[1] - 10.0/(1 + x[0])
The solution is sensitive to the starting conditions.
In [23]:
x0 = np.array([4, 2])
A = np.array([2,8])
B = np.array([8,4])
cons = {'type': 'eq', 'fun': g}
res = opt.minimize(f, x0, args=(A, B), constraints=cons)
res.x, res.fun
Out[23]:
(array([4.39881339, 1.85225887]), 10.792179122216428)
In [24]:
xp = np.linspace(0, 10, 100)
plt.scatter([A[0], B[0]], [A[1], B[1]])
plt.plot(xp, 10.0/(1 + xp), c='blue')
plt.plot([A[0], res.x[0], B[0]], [A[1], res.x[1], B[1]], c='red')
pass

We know that solutions must be along the river, so start with equally spaced points (in the x-direction) along the river.
In [25]:
x0s = [(x, 10/(1+x)) for x in range(11)]
In [26]:
best_x = None
best_fun = np.infty
A = np.array([2,8])
B = np.array([8,4])
cons = {'type': 'eq', 'fun': g}
for x0 in x0s:
res = opt.minimize(f, x0, args=(A, B), constraints=cons)
x, fun = res.x, res.fun
if fun < best_fun:
best_fun = fun
best_x = x
In [27]:
best_x, best_fun
Out[27]:
(array([0.53225961, 6.52630922]), 9.96339829956226)
In [28]:
xp = np.linspace(0, 10, 100)
plt.scatter([A[0], B[0]], [A[1], B[1]])
plt.plot(xp, 10.0/(1 + xp), c='blue')
plt.plot([A[0], best_x[0], B[0]], [A[1], best_x[1], B[1]], c='red')
pass

C. Find the minimum of the following quadratic function on \(\mathbb{R}^2\)
Under the constraints:
- Use a matrix decomposition method to find the minimum of the
unconstrained problem without using
scipy.optimize(Use library functions - no need to code your own). Note: for full credit you should exploit matrix structure. (3 points) - Find the solution using constrained optimization with the
scipy.optimizepackage. (3 points) - Use Lagrange multipliers and solving the resulting set of equations
directly without using
scipy.optimize. (4 points)
In [29]:
A = np.array([[13,5],[5,7]])
b = np.array([1.0,1.0]).T
c = 2
la.cho_solve(la.cho_factor(A), -b/2)
Out[29]:
array([-0.01515152, -0.06060606])
In [30]:
def f(x, A, b, c):
return x.T.dot(A).dot(x) + b.T.dot(x) + c
# check unconstrained solution
usol = opt.minimize(f, [0,0], args=(A, b, c))
usol.x
Out[30]:
array([-0.01515152, -0.06060606])
In [31]:
cons = ({'type': 'eq', 'fun': lambda x: 2*x[0] - 5*x[1] - 2},
{'type': 'eq', 'fun': lambda x: x[0] + x[1] - 1})
opt.minimize(f, [0,0], constraints=cons, args=(A, b, c))
Out[31]:
fun: 15.999999999999996
jac: array([26.99999976, 11.00000024])
message: 'Optimization terminated successfully.'
nfev: 14
nit: 3
njev: 3
status: 0
success: True
x: array([1.00000000e+00, 3.41607086e-16])
In [32]:
M = np.array([
[26, 10, 2, 1],
[10, 14, -5, 1],
[2, -5, 0, 0],
[1, 1, 0, 0]
])
y = np.array([-1, -1, 2, 1]).T
la.solve(M, y)
Out[32]:
array([ 1.00000000e+00, -4.37360585e-17, -2.28571429e+00, -2.24285714e+01])
3. Gradient descent¶
We observe some data points \((x_i, y_i)\), and believe that an appropriate model for the data is that
with some added noise. Find optimal values of the parameters \(\beta = (a, b, c)\) that minimize \(\Vert y - f(x) \Vert^2\)
- using
scipy.linalg.lstsq(10 points) - solving the normal equations \(X^TX \beta = X^Ty\) (10 points)
- using
scipy.linalg.svd(10 points) - using gradient descent with RMSProp (no bias correction) and starting with an initial value of \(\beta = \begin{bmatrix}1 & 1 & 1\end{bmatrix}\). Use a learning rate of 0.01 and 10,000 iterations. This should take a few seconds to complete. (25 points)
In each case, plot the data and fitted curve using matplotlib.
Data
x = array([ 3.4027718 , 4.29209002, 5.88176277, 6.3465969 , 7.21397852,
8.26972154, 10.27244608, 10.44703778, 10.79203455, 14.71146298])
y = array([ 25.54026428, 29.4558919 , 58.50315846, 70.24957254,
90.55155435, 100.56372833, 91.83189927, 90.41536733,
90.43103028, 23.0719842 ])
In [33]:
x = np.array([ 3.4027718 , 4.29209002, 5.88176277, 6.3465969 , 7.21397852,
8.26972154, 10.27244608, 10.44703778, 10.79203455, 14.71146298])
y = np.array([ 25.54026428, 29.4558919 , 58.50315846, 70.24957254,
90.55155435, 100.56372833, 91.83189927, 90.41536733,
90.43103028, 23.0719842 ])
In [34]:
def f(beta, x):
"""Model function."""
return beta[0]*x**2 + beta[1]*x**3 + beta[2]*np.sin(x)
In [35]:
X = np.c_[x**2, x**3, np.sin(x)]
Least squares solution¶
In [36]:
beta = np.linalg.lstsq(X, y, rcond=None)[0]
In [37]:
beta
Out[37]:
array([ 2.99259014, -0.19883227, 10.20024689])
In [38]:
plt.plot(x, y, 'o')
xp = np.linspace(0, 15, 100)
plt.plot(xp, f(beta, xp))
pass

Normal equations solution¶
In [39]:
beta = np.linalg.solve(X.T @ X, X.T @ y)
beta
Out[39]:
array([ 2.99259014, -0.19883227, 10.20024689])
In [40]:
plt.plot(x, y, 'o')
xp = np.linspace(0, 15, 100)
plt.plot(xp, f(beta, xp))
pass

SVD solution¶
In [41]:
U, s, Vt = np.linalg.svd(X)
beta = Vt.T @ np.diag(1/s) @ U[:, :len(s)].T @ y.reshape(-1,1)
beta
Out[41]:
array([[ 2.99259014],
[-0.19883227],
[10.20024689]])
In [42]:
plt.plot(x, y, 'o')
xp = np.linspace(0, 15, 100)
plt.plot(xp, f(beta, xp))
pass

Gradient descent solution (with ADAM)¶
In [43]:
def res(beta, x, y):
"""Resdiual funciton."""
return f(beta, x) - y
Scalar form for gradient¶
In [44]:
def grad(beta, x, y):
"""Gradient of function."""
return np.array([
np.sum(x**2 * res(beta, x, y)),
np.sum(x**3 * res(beta, x, y)),
np.sum(np.sin(x) * res(beta, x, y))
])
In [45]:
def gd(beta, x, y, f, grad, alpha=0.01, beta1=0.9, beta2=0.999, eps=1e-8):
"""Gradient descent."""
m = 0
v = 0
for i in range(10000):
m = beta1*m + (1-beta1)*grad(beta, x, y)
v = beta2*v + (1-beta2)*grad(beta, x, y)**2
mc = m/(1+beta1**(i+1))
vc = v/(1+beta2**(i+1))
beta = beta - alpha * m / (eps + np.sqrt(vc))
return beta
In [46]:
beta = gd(np.array([1,1,1]), x, y, f, grad)
beta
Out[46]:
array([ 2.99259014, -0.19883227, 10.20024689])
In [47]:
plt.plot(x, y, 'o')
xp = np.linspace(0, 15, 100)
plt.plot(xp, f(beta, xp))
pass

Matrix form for gradient¶
In [48]:
def grad_m(X, y, b):
return X.T@X@b - X.T@y
Check that both gradient functions give the same solution
In [49]:
grad(np.zeros(3), x, y)
Out[49]:
array([-5.23658157e+04, -5.13828104e+05, 1.02460119e+02])
In [50]:
X = np.c_[x**2, x**3, np.sin(x)]
grad_m(X, y, np.zeros(3))
Out[50]:
array([-5.23658157e+04, -5.13828104e+05, 1.02460119e+02])
In [51]:
def gd_m(beta, x, y, f, grad, alpha=0.01, beta1=0.9, beta2=0.999, eps=1e-8):
"""Gradient descent."""
m = 0
v = 0
X = np.c_[x**2, x**3, np.sin(x)]
for i in range(10000):
m = beta1*m + (1-beta1)*grad_m(X, y, beta)
v = beta2*v + (1-beta2)*grad_m(X, y, beta)**2
mc = m/(1+beta1**(i+1))
vc = v/(1+beta2**(i+1))
beta = beta - alpha * m / (eps + np.sqrt(vc))
return beta
In [52]:
beta = gd(np.array([1,1,1]), x, y, f, grad)
beta
Out[52]:
array([ 2.99259014, -0.19883227, 10.20024689])
In [53]:
plt.plot(x, y, 'o')
xp = np.linspace(0, 15, 100)
plt.plot(xp, f(beta, xp))
pass

In [ ]: