Statistics review 1: Presenting and summarising data

R code to accompany paper

Key learning points

• The first step in any analysis is to describe and summarize the data
• Understand the following
  • qualitative data (unordered and ordered) and quantitative data (discrete and continuous)
  • how these types of data can be represented figuratively
  • the two important features of a quantitative dataset (location and variability)
  • the measures of location (mean, median and mode)
  • the measures of variability (range, interquartile range, standard deviation and variance)
  • common distributions of clinical data
  • simple transformations of positively skewed data.

suppressPackageStartupMessages(library(tidyverse))

Set default plot size to 4” by 3”

options(repr.plot.width=4, repr.plot.height=3)

Summary Statistics

df1 <- read.csv('data/haemoglobin.csv', header=FALSE, col.names=c("hb"))

Working with data frames

class(df1)

'data.frame'

head(df1)

hb
5.4
8.2
6.4
8.3
6.4
8.3

str(df1)

'data.frame':       48 obs. of  1 variable:
 $ hb: num  5.4 8.2 6.4 8.3 6.4 8.3 7 8.6 7.1 8.8 ...

dim(df1)

1. 48
2. 1

summary(df1)

      hb
Min.   : 5.400
1st Qu.: 8.750
Median : 9.800
Mean   : 9.869
3rd Qu.:10.800
Max.   :14.100

Dataframe indexing

df1$hb

1. 5.4
2. 8.2
3. 6.4
4. 8.3
5. 6.4
6. 8.3
7. 7
8. 8.6
9. 7.1
10. 8.8
11. 7.3
12. 8.9
13. 7.7
14. 9.1
15. 8.1
16. 9.3
17. 9.3
18. 9.9
19. 9.4
20. 9.9
21. 9.4
22. 9.9
23. 9.4
24. 10.1
25. 9.4
26. 10.3
27. 9.5
28. 10.3
29. 9.7
30. 10.4
31. 9.7
32. 10.4
33. 10.5
34. 11.9
35. 10.5
36. 12.3
37. 10.6
38. 12.6
39. 10.8
40. 12.7
41. 10.8
42. 13
43. 11.3
44. 13.3
45. 11.7
46. 14
47. 11.7
48. 14.1

df1[,1]

1. 5.4
2. 8.2
3. 6.4
4. 8.3
5. 6.4
6. 8.3
7. 7
8. 8.6
9. 7.1
10. 8.8
11. 7.3
12. 8.9
13. 7.7
14. 9.1
15. 8.1
16. 9.3
17. 9.3
18. 9.9
19. 9.4
20. 9.9
21. 9.4
22. 9.9
23. 9.4
24. 10.1
25. 9.4
26. 10.3
27. 9.5
28. 10.3
29. 9.7
30. 10.4
31. 9.7
32. 10.4
33. 10.5
34. 11.9
35. 10.5
36. 12.3
37. 10.6
38. 12.6
39. 10.8
40. 12.7
41. 10.8
42. 13
43. 11.3
44. 13.3
45. 11.7
46. 14
47. 11.7
48. 14.1

df1[1,]

5.4

df1[5:10,]

1. 6.4
2. 8.3
3. 7
4. 8.6
5. 7.1
6. 8.8

Measuring location

Using a custom function

sr.mean <- function(x) {
    sum(x)/length(x)
}

sr.mean(df1$hb)

9.86875

Using built-in functions

df1 %>% summarize(mean=mean(hb), median=median(hb), mode=mode(hb))

mean	median	mode
9.86875	9.8	numeric

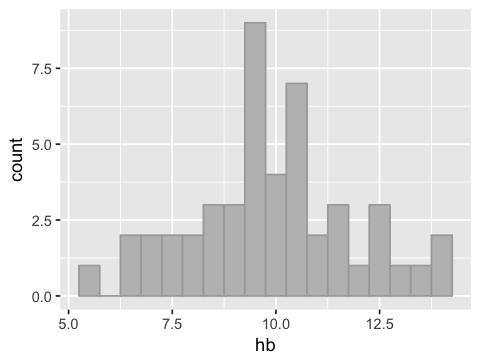
Visualizing the data distribution

ggplot(df1, aes(x=hb)) +
geom_histogram(binwidth=0.5, fill="grey", color="darkgrey")

Measuring variability

range(df1$hb)

1. 5.4
2. 14.1

quantile(df1$hb, c(0.25, 0.75))

25%

8.75

75%

10.8

sd(df1$hb)

1.97291837512189

var(df1$hb)

3.89240691489362

df1 %>% summarize(min=min(hb),
                 max=max(hb),
                 iqr=quantile(hb, 0.75)- quantile(hb, 0.25),
                 sd=sd(hb),
                 var=var(hb))

min	max	iqr	sd	var
5.4	14.1	2.05	1.972918	3.892407

Using a convenience function

summary(df1)

      hb
Min.   : 5.400
1st Qu.: 8.750
Median : 9.800
Mean   : 9.869
3rd Qu.:10.800
Max.   :14.100

Common distributions and simple transformations

Exercise. Read in the urea.csv data file into a data frame df2 and name the column urea.

df2 <- read.csv("data/urea.csv", header=FALSE, col.names=c("urea"))

head(df2, n=3)

urea
16.007049
13.647212
6.653046

g <- ggplot(df2, aes(x=urea))
g <- g + geom_histogram(binwidth=1, fill="grey", color="darkgrey")
g

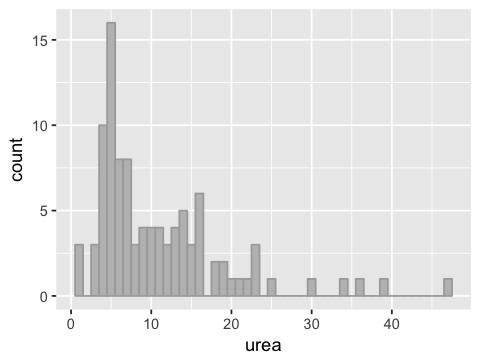
Skewness

We say the data has a positive or right skew. This name comes from the fact that there is a statistical measure called skewness that is positive for long right tails, and negative for long left tails.

install.packages("e1071", repos = "http://cran.r-project.org")
library(e1071)

The downloaded binary packages are in
    /var/folders/3l/tbmzdkss71152d8t9n1f8nx40000gn/T//RtmpdeIh9P/downloaded_packages

skewness(df2$urea)

1.80179083039024

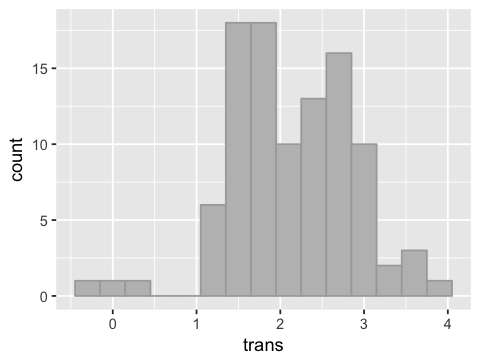
Log transform of the data

df2['trans'] = log(df2['urea'])

g <- ggplot(df2, aes(x=trans))
g <- g + geom_histogram(binwidth=0.3, fill="grey", color="darkgrey")
g

head(df2)

urea	trans
16.007049	2.773029
13.647212	2.613535
6.653046	1.895075
5.107674	1.630744
19.325193	2.961410
10.141074	2.316594

Finding geometric mean

gm  <- function(x) {
    return(exp(mean(log(x))))
}

df2 %>% summarise(mean=mean(urea), geom.mean=gm(urea))

mean	geom.mean
10.97242	8.504802

Exercise

1 Load the file “ph.csv” into a data frame called df. Label the column ph.

2. Plot a histogram of the data. Calculate the skewness of the ph column.

3 Left skewed data can sometimes be made more “normal” by an exponential transformation. That is, if the original data is \(x\), the transformed data is \(e^x\). Create another column named trasn with the transformed data.

4. Plot a histogram of the transformed data.

5 Write your own function called sr.sd to calculate the standard deviation using the formula in Table 3.

6. Create a new table using the summarise function with the mean and standard deviation of both original and transformed data values. This data frame should have 1 row and 4 columns named orig.mean, orig.sd, trans.mean, trans.sd.