Statistics review 8: Qualitative data – tests of association¶
R code accompanying paper)
Key learning points¶
- How to investigate relationships between two qualitative (categorical) variables
- \(\chi^2\) test of association
- Test for trend (one variable is ordinal)
- Risk measurement
- Evaluating proportions
suppressPackageStartupMessages(library(tidyverse))
options(repr.plot.width=4, repr.plot.height=3)
Categorical data¶
Unordered¶
- sex
- blood group
- classification of disease
- whether the patient survived
Ordinal¶
- Age group
- Clinical scales (e.g. Pain scale)
\(\chi^2\) test of association¶
none <- c(686, 451, 168)
exit <- c(152, 35, 58)
bacteremia <- c(96, 38, 22)
o <- data.frame(none=none, exit=exit, bacteremia=bacteremia,
row.names= c("jugular", "subclavian", "femoral"))
Observed counts¶
o
| none | exit | bacteremia | |
|---|---|---|---|
| jugular | 686 | 152 | 96 |
| subclavian | 451 | 35 | 38 |
| femoral | 168 | 58 | 22 |
m <- addmargins(as.matrix(o))
m
| none | exit | bacteremia | Sum | |
|---|---|---|---|---|
| jugular | 686 | 152 | 96 | 934 |
| subclavian | 451 | 35 | 38 | 524 |
| femoral | 168 | 58 | 22 | 248 |
| Sum | 1305 | 245 | 156 | 1706 |
Expected counts¶
e <- outer(m[1:3,4], m[4,1:3]/m[4,4])
round(e, 1)
| none | exit | bacteremia | |
|---|---|---|---|
| jugular | 714.5 | 134.1 | 85.4 |
| subclavian | 400.8 | 75.3 | 47.9 |
| femoral | 189.7 | 35.6 | 22.7 |
Calculate \(\chi^2\) test statistic¶
T <- sum((o - e)^2/e)
round(T, 2)
df <- (nrow(o) -1) * (ncol(o) - 1)
df
Calculate p-value from \(\chi^2\) distribution¶
1 - pchisq(T, df)
Use built in test¶
chisq.test(o)
Pearson's Chi-squared test
data: o
X-squared = 51.262, df = 4, p-value = 1.968e-10
Residuals¶
t <- addmargins(as.matrix(prop.table(o)))
t
| none | exit | bacteremia | Sum | |
|---|---|---|---|---|
| jugular | 0.40211020 | 0.08909730 | 0.05627198 | 0.5474795 |
| subclavian | 0.26436108 | 0.02051583 | 0.02227433 | 0.3071512 |
| femoral | 0.09847597 | 0.03399766 | 0.01289566 | 0.1453693 |
| Sum | 0.76494725 | 0.14361079 | 0.09144197 | 1.0000000 |
Adjusted standardized residues¶
The numbers don’t agree with table 4 in the paper. Student to check by hand calculations?
round((o - e)/sqrt(e*(1-t[1:3,4])*(1-t[4,1:3])), 1)
| none | exit | bacteremia | |
|---|---|---|---|
| jugular | -3.3 | 4.7 | 3.5 |
| subclavian | 3.3 | -6.0 | -1.9 |
| femoral | -1.8 | 4.3 | -0.2 |
Two by two tables¶
treatment <- c(3, 47)
control <- c(8, 37)
df1 <- data.frame(treatment=treatment, contorl=control)
df1
| treatment | contorl |
|---|---|
| 3 | 8 |
| 47 | 37 |
chisq.test(df1, correct = FALSE)
Pearson's Chi-squared test
data: df1
X-squared = 3.2089, df = 1, p-value = 0.07324
Fisher’s exact test¶
fisher.test(df1)
Fisher's Exact Test for Count Data
data: df1
p-value = 0.1083
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.04775944 1.35642029
sample estimates:
odds ratio
0.2989279
Yates’ continuity correction¶
chisq.test(df1, correct=TRUE)
Pearson's Chi-squared test with Yates' continuity correction
data: df1
X-squared = 2.1617, df = 1, p-value = 0.1415
Test for trend¶
alert <- c(1110, 108)
vopr <- c(54, 14)
unresponsive <- c(14, 6)
df2 <- data.frame(alert=alert, vopr=vopr, unresponsive=unresponsive,
row.names=c("sruvived", "died"))
df2
| alert | vopr | unresponsive | |
|---|---|---|---|
| sruvived | 1110 | 54 | 14 |
| died | 108 | 14 | 6 |
chisq.test(df2)
Warning message in chisq.test(df2):
“Chi-squared approximation may be incorrect”
Pearson's Chi-squared test
data: df2
X-squared = 19.383, df = 2, p-value = 6.18e-05
Calling the trend test¶
The trend test takes two arguments
- Number of events
- Number of trials
So we have to a little massaging to get the data in the correct format.
We can use either row as the number of events¶
Using number of survivors.
prop.trend.test(as.matrix(df2[1,]), colSums(df2))
Chi-squared Test for Trend in Proportions
data: as.matrix(df2[1, ]) out of colSums(df2) ,
using scores: 1 2 3
X-squared = 19.328, df = 1, p-value = 1.101e-05
Using number of deaths.
prop.trend.test(as.matrix(df2[2,]), colSums(df2))
Chi-squared Test for Trend in Proportions
data: as.matrix(df2[2, ]) out of colSums(df2) ,
using scores: 1 2 3
X-squared = 19.328, df = 1, p-value = 1.101e-05
Interpretation as slope of linear regression model¶
points <- c(replicate(1110, c(1,1)), replicate(108, c(1,2)),
replicate(54, c(2,1)), replicate(14, c(2,2)),
replicate(14, c(3,1)), replicate(6, c(3,2)))
length(points)
df3 <- data.frame(matrix(points, ncol=2, byrow = T))
colnames(df3) <- c("x", "y")
summary(lm(y ~ x - 1 , data=df3))
Call:
lm(formula = y ~ x - 1, data = df3)
Residuals:
Min 1Q Median 3Q Max
-1.81677 0.06108 0.06108 0.06108 1.06108
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x 0.938922 0.009996 93.93 <2e-16 *
---
Signif. codes: 0 ‘*’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4085 on 1305 degrees of freedom
Multiple R-squared: 0.8711, Adjusted R-squared: 0.871
F-statistic: 8822 on 1 and 1305 DF, p-value: < 2.2e-16
ggplot(df3, aes(x=x, y=y)) + geom_jitter(width = .3, height=.3) +
geom_smooth(method="lm") +
scale_x_continuous(breaks=1:3, labels=c("alert", "vopr", "unresp")) +
scale_y_continuous(breaks=1:2, labels=c("survided", "died")) +
xlab("") + ylab("")
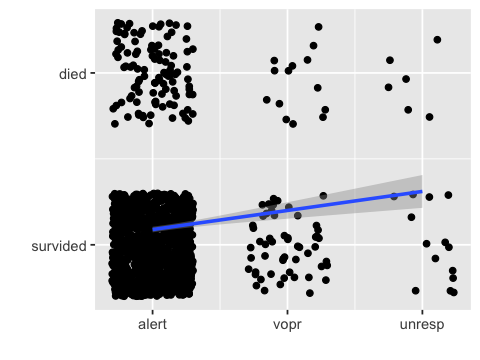
Measurement of risk¶
died <- c(38, 59)
survived <- c(79, 60)
df4 <- data.frame(died=died, survived=survived, row.names=c("early", "standard"))
df4
| died | survived | |
|---|---|---|
| early | 38 | 79 |
| standard | 59 | 60 |
round(100*df4[1,1]/sum(df4[1,]), 1)
round(100*df4[2,1]/sum(df4[2,]), 1)
round(df4[1,1]/sum(df4[1,2]), 2)
round(df4[2,1]/sum(df4[2,2]), 2)
Confidence interval for a proportion¶
Confidence interval for death with early treatment¶
n <- sum(df4[1,])
p <- df4[1,1]/n
alpha <- 0.05
k <- qnorm(1 - alpha/2)
se <- sqrt(p*(1-p)/n)
round(100*c(p - k*se, p + k*se), 1)
- 24
- 41
Confidence interval for death with early treatment¶
n <- sum(df4[2,])
p <- df4[2,1]/n
alpha <- 0.05
k <- qnorm(1 - alpha/2)
se <- sqrt(p*(1-p)/n)
round(100*c(p - k*se, p + k*se), 1)
- 40.6
- 58.6
Testing for difference between two proportions¶
df4
| died | survived | |
|---|---|---|
| early | 38 | 79 |
| standard | 59 | 60 |
df4 <- df4 %>% mutate(total=died+survived)
df4
| died | survived | total |
|---|---|---|
| 38 | 79 | 117 |
| 59 | 60 | 119 |
prop.test(df4[,1], df4[,3], correct = FALSE)
2-sample test for equality of proportions without continuity
correction
data: df4[, 1] out of df4[, 3]
X-squared = 7.1271, df = 1, p-value = 0.007593
alternative hypothesis: two.sided
95 percent confidence interval:
-0.29458384 -0.04744015
sample estimates:
prop 1 prop 2
0.3247863 0.4957983
Matched samples¶
breath_plus <- c(40, 4)
breath_minus <- c(8, 32)
df5 <- data.frame(breath_plus=breath_plus, breath_minus=breath_minus,
row.names=c("xxoid_plus", "oxoid_minus"))
df5
| breath_plus | breath_minus | |
|---|---|---|
| xxoid_plus | 40 | 8 |
| oxoid_minus | 4 | 32 |
Using built in test¶
mcnemar.test(as.matrix(df5))
McNemar's Chi-squared test with continuity correction
data: as.matrix(df5)
McNemar's chi-squared = 0.75, df = 1, p-value = 0.3865
Exercises¶
suppressPackageStartupMessages(library(MASS))
The rows indicate smoking history, and the columns indicate frequency of exercise¶
The allowed values in Smoke are “Heavy”, “Regul” (regularly), “Occas” (occasionally) and “Never”, and “Freq” (frequently), “Some” and “None” for Exercise.
tbl = table(survey$Smoke, survey$Exer)
tbl
Freq None Some
Heavy 7 1 3
Never 87 18 84
Occas 12 3 4
Regul 9 1 7
1. Is there a evidence for a relationship between smoking history and frequency of exercise? Solve this a) by manual calculation, and b) by using the chisq.test.
2. Is there evidence for a trend for exercise with frequency of smoking if we consider smoking as an ordinal variables?
3. Create a new table that uses only the (Freq, None) columns and (Heavy, Never) rows. Compare the results of the \(\chi^2\) test with and without Yates continuity correction, as well as the Fisher exact test.