C++¶
A brief introduction to features of C++ that are not found in C, using
C++11 features where possible. As usual, we will exclude classes and any
discussion of object-oriented programming. You might have to add the
appropriate #include statements to compile some of these code
snippets.
Also see the section on pybind11 for how to easily wrap C++ code so that it can be called from Python.
Hello, world¶
Note the use of the iostream library and the standard namepace
qualification std::cout.
#include <iostream>
int main()
{
std::cout << "Hello, world!\n";
}
Streaming¶
#include <fstream>
#include <iostream>
#include <memory>
int main(int argc, char* argv[]) {
int size;
if (argc == 2) {
size = atoi(argv[1]);
} else {
size = 3;
}
// writing to output file stream
std::ofstream fout("data/numbers.txt");
for (int i = 0; i < size; ++i) {
fout << i << "\n";
}
fout.close();
// declare dynamic array of integers using unique_ptr
std::unique_ptr<int[]> arr{new int[size]};
// write from input file stream to array
std::ifstream fin("data/numbers.txt");
for (int i = 0; i < size; ++i) {
fin >> arr[i];
}
fin.close();
// send array to standard output using ranged for loop
for (int i = 0; i < size; i++) {
std::cout << arr[i] << "\n";
}
}
Namespaces¶
Just like Python, C++ has namespaces that allow us to build large
libraries without worrying about name collisions. In the Hello world
program, we used the explicit name std::cout indicating that
cout is a member of the standard workspace. We can also use the
using keyword to import selected functions or classes from a
namespace.
using std::cout;
int main()
{
cout << "Hello, world!\n";
}
For small programs, we sometimes import the entire namespace for convenience, but this may cause namespace collisions in larger programs.
using namespace std;
int main()
{
cout << "Hello, world!\n";
}
You can easily create your own namespace.
namespace sta_663 {
const double pi=2.14159;
void greet(string name) {
cout << "\nTraditional first program\n";
cout << "Hello, " << name << "\n";
}
}
int main()
{
cout << "\nUsing namespaces\n";
string name = "Tom";
cout << sta_663::pi << "\n";
sta_663::greet(name);
}
Looping¶
Note the traditional for loop and the new range for loop. There is also
a while loop (not shown).
// for loops
int main()
{
int x[] = {1, 2, 3, 4, 5};
cout << "\nTraditional for loop\n";
for (int i=0; i < sizeof(x)/sizeof(x[0]); i++) {
cout << i << endl;
}
cout << "\nRanged for loop\n\n";
for (const auto &i : x) {
cout << i << endl;
}
}
Exercise 1
Use loop to generate the 12 by 12 times table. Compile and run. You don’t have to worry much about formatting, but the output should have 12 rows with numbers separated by spaces.
In [1]:
%%file ex1.cpp
#include <iostream>
#include <iomanip>
int main()
{
for (int i=1; i<=12; i++) {
for (int j=1; j<=12; j++) {
std::cout << std::setw(3) << i*j << ' ';
}
std::cout << "\n";
}
}
Overwriting ex1.cpp
In [2]:
%%bash
g++ ex1.cpp -o ex1
In [3]:
%%bash
./ex1
1 2 3 4 5 6 7 8 9 10 11 12
2 4 6 8 10 12 14 16 18 20 22 24
3 6 9 12 15 18 21 24 27 30 33 36
4 8 12 16 20 24 28 32 36 40 44 48
5 10 15 20 25 30 35 40 45 50 55 60
6 12 18 24 30 36 42 48 54 60 66 72
7 14 21 28 35 42 49 56 63 70 77 84
8 16 24 32 40 48 56 64 72 80 88 96
9 18 27 36 45 54 63 72 81 90 99 108
10 20 30 40 50 60 70 80 90 100 110 120
11 22 33 44 55 66 77 88 99 110 121 132
12 24 36 48 60 72 84 96 108 120 132 144
Functions and Lambdas¶
// simple funciton
int add0(int a, int b) {
return a + b;
}
// simple function with reference variables
void add1(int a, int b, int& c) {
c = a + b;
}
// lambda function
auto add2 = [] (int a, int b) { return a + b; };
int main() {
cout << "\nStandard function\n";
int a = 3, b = 4;
cout << add0(a, b) << endl;
int c = 0;
cout << "\nStandard with reference varaibles\n";
add1(a, b, c);
cout << c << endl;
cout << "\nLambda function\n";
cout << add2(a, b) << endl;
auto add3 = [c] (int a, int b) { return c * add2(a, b); };
c -= 5;
cout << "\nLambda function with value capture\n";
cout << add3(a, b) << endl;
auto add4 = [&c] (int a, int b) { return c * add2(a, b); };
cout << "\nLambda function with reference capture\n";
cout << add4(a, b) << endl;
}
Templates¶
// templates
template <typename T>
T add5(T a, T b) { return a + b; }
int main()
{
cout << "\nTemplate function with ints\n";
cout << add5(3, 4) << endl;
cout << "\nTemplate function with doubles\n";
cout << add5(3.14, 2.78) << endl;
}
Iterators¶
int main()
{
int x[] = {1, 2, 3, 4, 5};
cout << "\nUsing iterators\n";
for (auto it=begin(x); it != end(x); it++) {
cout << *it << endl;
}
}
Containers¶
int main()
{
vector<double> v = {1,2,3};
cout << "\nUsing the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
v.push_back(4);
v.push_back(5);
cout << "\nGrowing the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
v.pop_back();
cout << "\nShrinking the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
cout << "\nUsing the unordered_map container\n";
unordered_map<string, int> dict = { {"ann", 23}, {"bob", 32}, {"charles", 17}};
dict["doug"] = 30;
for (auto it=begin(dict); it != end(dict); it++) {
cout << it->first << ", " << it->second << endl;
}
cout << dict["bob"] << endl;
}
Using iterators to write generic template functions¶
In header file:
using std::accumulate;
using std::transform;
using std::inner_product;
using std::vector;
using std::distance;
template<typename Iter>
auto sum(Iter first, Iter last) {
return accumulate(first, last, 0.0);
};
template<typename Iter>
auto mean(Iter first, Iter last) {
return sum(first, last)/distance(first, last);
};
template<typename Iter>
auto sd(Iter first, Iter last) {
auto mu = mean(first, last);
vector<double> v1(distance(first, last));
transform(first, last, begin(v1), [mu](double x) { return x - mu; });
return sqrt(inner_product(begin(v1), end(v1), begin(v1), 0.0)/v1.size());
};
In source file:
#include <iostream>
#include "vector_templates_2.h"
using namespace std;
int main() {
// use array of float instead of vector of double
float v1[] = {10.0, 20.0, 30.0};
cout << "Sum is " << sum(begin(v1), end(v1)) << endl;
cout << "Mean is " << mean(begin(v1), end(v1)) << endl;
cout << "SD is " << sd(begin(v1), end(v1)) << endl;
for (auto &x : v1) {
cout << x << " ";
}
cout << endl;
}
Exercise 2
Write a function that takes a vector of doubles returns the squared vector. Compile and run the function with the initial vector containing 1.0, 2.0, 3.0, 4.0, 5.0.
In [4]:
%%file ex2.cpp
#include <iostream>
#include <vector>
using std::vector;
using std::cout;
vector<double> squares(vector<double> xs) {
vector<double> ys(xs.size());
for (int i=0; i<ys.size(); i++) {
ys[i] = xs[i] * xs[i];
}
return ys;
}
int main()
{
vector<double> xs = {1.0, 2.0, 3.0, 4.0, 5.0};
auto ys = squares(xs);
for (auto& y: ys) {
cout << y << ", ";
}
cout << "\n";
}
Overwriting ex2.cpp
In [5]:
%%bash
g++ -std=c++11 ex2.cpp -o ex2
In [6]:
%%bash
./ex2
1, 4, 9, 16, 25,
EXercise 3
Convert the function from Exercise 2 so that it works for lists or vectors of ints, floats and doubles.
In [7]:
%%file ex3.cpp
#include <iostream>
#include <vector>
using std::vector;
using std::cout;
template<typename T>
vector<T> squares(vector<T> xs) {
vector<T> ys(xs.size());
for (int i=0; i<ys.size(); i++) {
ys[i] = xs[i] * xs[i];
}
return ys;
}
int main()
{
vector<int> xs = {1, 2, 3, 4, 5};
auto ys = squares(xs);
for (auto& y: ys) {
cout << y << ", ";
}
cout << "\n";
}
Overwriting ex3.cpp
In [8]:
%%bash
./ex3
1, 4, 9, 16, 25,
Algorithms¶
int main()
{
void show_algorithms() {
vector<int> v(10, 0);
cout << "\nWorking with standard library algorithm\n";
cout << "\nInitial state\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << " ";
}
cout << endl;
cout << "\nAfter iota\n";
iota(begin(v), end(v), 5);
for (auto it=begin(v); it != end(v); it++) {
cout << *it << " ";
}
cout << endl;
cout << "\nSimple accumulate\n";
int s = accumulate(begin(v), end(v), 0);
cout << s << endl;
cout << "\nAccumulate with custom sum of squares reduction\n";
int t = accumulate(begin(v), end(v), 0, [] (int acc, int x) { return acc + x*x; });
cout << t << endl;
}
Exercise 4
Write a function to calculate the mean of a vector of numbers using
accumulate from the <numeric> library. Compile and test with
some vectors.
In [9]:
%%file ex4.cpp
#include <iostream>
#include <vector>
#include <numeric>
using std::vector;
using std::cout;
template<typename T>
double mean(vector<T> xs) {
double s = std::accumulate(begin(xs), end(xs), 0);
return s/xs.size();
}
int main()
{
vector<double> xs = {1, 2, 3, 4, 5};
double mu = mean(xs);
cout << mu << "\n";
}
Overwriting ex4.cpp
In [10]:
%%bash
g++ -std=c++11 ex4.cpp -o ex4
In [11]:
%%bash
./ex4
3
Function pointers¶
Example 1:
int main()
{
cout << "\nUsing generalized function pointers\n";
using func = function<double(double, double)>;
auto f1 = [](double x, double y) { return x + y; };
auto f2 = [](double x, double y) { return x * y; };
auto f3 = [](double x, double y) { return x + y*y; };
double x = 3, y = 4;
vector<func> funcs = {f1, f2, f3,};
for (auto& f : funcs) {
cout << f(x, y) << "\n";
}
}
Example 2:
#include <iostream>
#include <vector>
#include <numeric>
#include <cmath>
#include <map>
#include <functional>
#include <string>
using namespace std;
double sum(vector<double> &v) {
return accumulate(begin(v), end(v), 0.0);
};
double mean(vector<double> &v) {
return sum(v)/v.size();
};
double sd(vector<double> &v) {
double mu = mean(v);
vector<double> v1(v.size());
transform(begin(v), end(v), begin(v1), [mu](double x) { return x - mu; });
return sqrt(inner_product(begin(v1), end(v1), begin(v1), 0.0)/v1.size());
};
int main() {
// alias func to a function wrapper
using func = function<double(vector<double> &)>;
// Assigning a lambda to a function wrapper
func first = [](vector<double>& v) { return v[0]; };
map<string, func> funcs{
{"Sum", sum},
{"Mean", mean},
{"SD", sd},
{"First", first}
};
vector<double> v1{10.0, 20.0, 30.0};
for (const auto &f : funcs) {
cout << f.first << " is " << f.second(v1) << endl;
}
}
Function templates are not functions¶
In header file
#pragma once
#include <iostream>
#include <vector>
#include <numeric>
#include <cmath>
using std::begin;
using std::end;
using std::accumulate;
using std::transform;
using std::inner_product;
using std::vector;
template<typename T>
T sum(vector<T> &v) {
return accumulate(begin(v), end(v), T{});
};
template<typename T>
T mean(vector<T> &v) {
return sum(v)/v.size();
};
template<typename T>
T sd(vector<T> &v) {
T mu = mean(v);
vector<T> v1(v.size());
transform(begin(v), end(v), begin(v1), [mu](T x) { return x - mu; });
return sqrt(inner_product(begin(v1), end(v1), begin(v1), T{})/v1.size());
};
In implementation file:
#include <iostream>
#include "vector_templates.h"
#include <functional>
#include <map>
using namespace std;
int main() {
using real = double;
using func = function<double(vector<double> &)>;
map<string, func> funcs{
// A function template is not a function
// So we need to instantiate it
{"Sum", sum<real>},
{"Mean", mean<real>},
{"SD", sd<real>}
};
vector<real> v1{10.0, 20.0, 30.0};
for (const auto &f : funcs) {
cout << f.first << " is " << f.second(v1) << endl;
}
}
Exercise 5
Implement Newton’s method in 1D for root finding. Pass in the function and gradient as generalized function pointers. Use the method to find all roots of the polynomial equation \(f(x) = x^3 - 7x - 6\)
In [1]:
%%file ex5.cpp
#include <iostream>
#include <vector>
#include <numeric>
#include <iomanip>
#include <cmath>
#include <functional>
using std::vector;
using std::cout;
using std::function;
using func = function<double(double)>;
double newton(double x0, func f, func grad, int max_iter=10) {
double x = x0;
for (int i=0; i<max_iter; i++) {
x -= f(x)/grad(x);
}
return x;
}
int main()
{
auto f = [](double x) { return pow(x, 3) - 7*x - 6; };
auto grad = [](double x) { return 3.0*pow(x, 2) - 7; };
vector<double> x = {-5, 0, 5};
for (auto& x0: x) {
cout << std::setw(2) << x0 << ": " << std::setw(3) << newton(x0, f, grad) << "\n";
}
}
Writing ex5.cpp
In [2]:
%%bash
g++ -std=c++11 ex5.cpp -o ex5
In [3]:
%%bash
./ex5
-5: -2
0: -1
5: 3
Random numbers¶
C++ now comes with its own collection of random number generators and quite a broad selection of distributions. See here for a great explanation.
int main()
{
cout << "\nGenerating random numbers\n";
// start random number engine wiht fixed seed
default_random_engine re{12345};
uniform_int_distribution<int> uniform(1,6); // lower and upper bounds
poisson_distribution<int> poisson(30); // rate
student_t_distribution<double> t(10); // degrees of freedom
auto runif = bind (uniform, re);
auto rpois = bind(poisson, re);
auto rt = bind(t, re);
for (int i=0; i<10; i++) {
cout << runif() << ", " << rpois() << ", " << rt() << "\n";
}
}
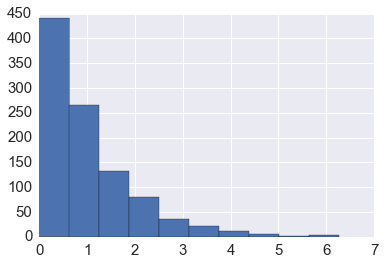
Exercise 6
Generate 1000 random points from the exponential distribution and save
as a comma-separated values (CSV) file. Open the file in Python and plot
the distribution using plt.hist.
In [15]:
%%file ex6.cpp
#include <fstream>
#include <random>
#include <iomanip>
using std::ofstream;
using std::default_random_engine;
using std::exponential_distribution;
int main()
{
// start random number engine wiht fixed seed
default_random_engine re;
re.seed(12345);
exponential_distribution<double> exponential(1.0);
auto rexp = bind (exponential, re);
int n = 1000;
ofstream fout("rexp.csv");
fout << rexp();
for (int i=1; i<n; i++) {
fout << "," << rexp();
}
fout << "\n";
}
Overwriting ex6.cpp
In [16]:
%%bash
g++ -std=c++11 ex6.cpp -o ex6
In [17]:
%%bash
./ex6
In [18]:
xs = np.loadtxt('rexp.csv', delimiter=',')
plt.hist(xs)
pass
Numeric library¶
Armadillo is an accessible library for doing numeric operations, much
like numpy in Python. Please see official
documentation for details. It
provides vectors, matrices, tensors, linear algebra, statistical
functions and a limited set of convenient random number generators.
int main()
{
using namespace arma;
vec u = linspace<vec>(0,1,5);
vec v = ones<vec>(5);
mat A = randu<mat>(4,5); // uniform random deviates
mat B = randn<mat>(4,5); // normal random deviates
cout << "\nVecotrs in Armadillo\n";
cout << u << endl;
cout << v << endl;
cout << u.t() * v << endl;
cout << "\nRandom matrices in Armadillo\n";
cout << A << endl;
cout << B << endl;
cout << A * B.t() << endl;
cout << A * v << endl;
cout << "\nQR in Armadillo\n";
mat Q, R;
qr(Q, R, A.t() * A);
cout << Q << endl;
cout << R << endl;
}
Exercise 7
Use the armadillo library to
- Generate 10 x-coordinates linearly spaced between 10 and 15
- Generate 10 random y-values as \(y = 3x^2 - 7x + 2 + \epsilon\) where \(\epsilon \sim 10 N(0,1)\)
- Find the length of \(x\) and \(y\) and the Euclidean distance between \(x\) and \(y\)
- Find the correlation between \(x\) and \(y\)
- Solve the linear system to find a quadratic fit for this data
In [4]:
%%file ex7.cpp
#include <iostream>
#include <fstream>
#include <armadillo>
using std::cout;
using std::ofstream;
int main()
{
using namespace arma;
vec x = linspace<vec>(10.0,15.0,10);
vec eps = 10*randn<vec>(10);
vec y = 3*x%x - 7*x + 2 + eps;
cout << "x:\n" << x << "\n";
cout << "y:\n" << y << "\n";
cout << "Lenght of x is: " << norm(x) << "\n";
cout << "Lenght of y is: " << norm(y) << "\n";
cout << "Distance(x, y) is: " << norm(x -y) << "\n";
cout << "Correlation(x, y) is: " << cor(x, y) << "\n";
mat A = join_rows(ones<vec>(10), x);
A = join_rows(A, x%x);
cout << "A:\n" << A << "\n";
vec b = solve(A, y);
cout << "b:\n" << b << "\n";
ofstream fout1("x.txt");
x.print(fout1);
ofstream fout2("y.txt");
y.print(fout2);
ofstream fout3("b.txt");
b.print(fout3);
}
Writing ex7.cpp
In [5]:
%%bash
g++ -std=c++11 ex7.cpp -o ex7 -larmadillo
In [6]:
%%bash
./ex7
x:
10.0000
10.5556
11.1111
11.6667
12.2222
12.7778
13.3333
13.8889
14.4444
15.0000
y:
2.4802e+02
2.6412e+02
2.9157e+02
3.3056e+02
3.4089e+02
3.9573e+02
4.4029e+02
4.7583e+02
5.2827e+02
5.8404e+02
Lenght of x is: 39.8493
Lenght of y is: 1280.16
Distance(x, y) is: 1240.76
Correlation(x, y) is: 0.9887
A:
1.0000e+00 1.0000e+01 1.0000e+02
1.0000e+00 1.0556e+01 1.1142e+02
1.0000e+00 1.1111e+01 1.2346e+02
1.0000e+00 1.1667e+01 1.3611e+02
1.0000e+00 1.2222e+01 1.4938e+02
1.0000e+00 1.2778e+01 1.6327e+02
1.0000e+00 1.3333e+01 1.7778e+02
1.0000e+00 1.3889e+01 1.9290e+02
1.0000e+00 1.4444e+01 2.0864e+02
1.0000e+00 1.5000e+01 2.2500e+02
b:
5.8621e+02
-1.0156e+02
6.7586e+00
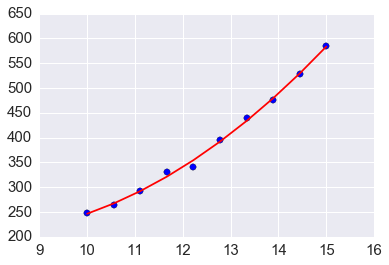
In [7]:
x = np.loadtxt('x.txt')
y = np.loadtxt('y.txt')
b = np.loadtxt('b.txt')
plt.scatter(x, y, s=40)
plt.plot(x, b[0] + b[1]*x + b[2]*x**2, c='red')
pass
Collected source code¶
In [23]:
%%file main.cpp
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <numeric>
#include <iterator>
#include <functional>
#include <random>
#include <armadillo>
using namespace std;
/* Topics
*
* - for loop
*
*
* - functions
* - lambdas
* - templates
*
* - iterators
* - containers
* - algorithms
* - Armadillo
*/
// hello world
void show_hello() {
cout << "Hello, world!\n";
}
namespace sta_663 {
const double pi=2.14159;
void greet(string name) {
cout << "\nTraditional first program\n";
cout << "Hello, " << name << "\n";
}
}
void show_namespace() {
cout << "\nUsing namespaces\n";
string name = "Tom";
cout << sta_663::pi << "\n";
sta_663::greet(name);
}
// for loops
void show_for() {
int x[] = {1, 2, 3, 4, 5};
cout << "\nTraditional for loop\n";
for (int i=0; i < sizeof(x)/sizeof(x[0]); i++) {
cout << i << endl;
}
cout << "\nRanged for loop\n\n";
for (auto &i : x) {
cout << i << endl;
}
}
// simple funciton
int add0(int a, int b) {
return a + b;
}
// simple function with reference variables
void add1(int a, int b, int& c) {
c = a + b;
}
// lambda function
auto add2 = [] (int a, int b) { return a + b; };
void show_func() {
cout << "\nStandard function\n";
int a = 3, b = 4;
cout << add0(a, b) << endl;
int c = 0;
cout << "\nStandard with reference varaibles\n";
add1(a, b, c);
cout << c << endl;
cout << "\nLambda function\n";
cout << add2(a, b) << endl;
auto add3 = [c] (int a, int b) { return c * add2(a, b); };
c -= 5;
cout << "\nLambda function with value capture\n";
cout << add3(a, b) << endl;
auto add4 = [&c] (int a, int b) { return c * add2(a, b); };
cout << "\nLambda function with reference capture\n";
cout << add4(a, b) << endl;
}
// templates
template <typename T>
T add5(T a, T b) { return a + b; }
void show_template() {
cout << "\nTemplate function with ints\n";
cout << add5(3, 4) << endl;
cout << "\nTemplate function with doubles\n";
cout << add5(3.14, 2.78) << endl;
}
void show_iterators() {
int x[] = {1, 2, 3, 4, 5};
cout << "\nUsing iterators\n";
for (auto it=begin(x); it != end(x); it++) {
cout << *it << endl;
}
}
void show_containers() {
vector<double> v = {1,2,3};
cout << "\nUsing the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
v.push_back(4);
v.push_back(5);
cout << "\nGrowing the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
v.pop_back();
cout << "\nShrinking the vector container\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << endl;
}
cout << "\nUsing the unordered_map container\n";
unordered_map<string, int> dict = { {"ann", 23}, {"bob", 32}, {"charles", 17}};
dict["doug"] = 30;
for (auto it=begin(dict); it != end(dict); it++) {
cout << it->first << ", " << it->second << endl;
}
cout << dict["bob"] << endl;
}
void show_algorithms() {
vector<int> v(10, 0);
cout << "\nWorking with standard library algorithm\n";
cout << "\nInitial state\n";
for (auto it=begin(v); it != end(v); it++) {
cout << *it << " ";
}
cout << endl;
cout << "\nAfter iota\n";
iota(begin(v), end(v), 5);
for (auto it=begin(v); it != end(v); it++) {
cout << *it << " ";
}
cout << endl;
cout << "\nSimple accumulate\n";
int s = accumulate(begin(v), end(v), 0);
cout << s << endl;
cout << "\nAccumulate with custom sum of squares reduction\n";
int t = accumulate(begin(v), end(v), 0, [] (int acc, int x) { return acc + x*x; });
cout << t << endl;
}
void show_functional() {
cout << "\nUsing generalized function pointers\n";
using func = function<double(double, double)>;
auto f1 = [](double x, double y) { return x + y; };
auto f2 = [](double x, double y) { return x * y; };
auto f3 = [](double x, double y) { return x + y*y; };
double x = 3, y = 4;
vector<func> funcs = {f1, f2, f3,};
for (auto& f : funcs) {
cout << f(x, y) << "\n";
}
}
void show_random() {
cout << "\nGenerating random numbers\n";
// start random number engine wiht fixed seed
default_random_engine re{12345};
uniform_int_distribution<int> uniform(1,6); // lower and upper bounds
poisson_distribution<int> poisson(30); // rate
student_t_distribution<double> t(10); // degrees of freedom
auto runif = bind (uniform, re);
auto rpois = bind(poisson, re);
auto rt = bind(t, re);
for (int i=0; i<10; i++) {
cout << runif() << ", " << rpois() << ", " << rt() << "\n";
}
}
void show_amrmadillo() {
using namespace arma;
vec u = linspace<vec>(0,1,5);
vec v = ones<vec>(5);
mat A = randu<mat>(4,5);
mat B = randn<mat>(4,5);
cout << "\nVecotrs in Armadillo\n";
cout << u << endl;
cout << v << endl;
cout << u.t() * v << endl;
cout << "\nRandom matrices in Armadillo\n";
cout << A << endl;
cout << B << endl;
cout << A * B.t() << endl;
cout << A * v << endl;
cout << "\nQR in Armadillo\n";
mat Q, R;
qr(Q, R, A.t() * A);
cout << Q << endl;
cout << R << endl;
}
int main() {
show_hello();
show_namespace();
show_for();
show_func();
show_template();
show_iterators();
show_containers();
show_algorithms();
show_functional();
show_random();
show_amrmadillo();
}
Overwriting main.cpp
Compilation¶
In [1]:
%%bash
g++ -std=c++11 -o main ex6.cpp -larmadillo
Execution¶
In [2]:
%%bash
./main
x:
10.0000
10.5556
11.1111
11.6667
12.2222
12.7778
13.3333
13.8889
14.4444
15.0000
y:
2.4802e+02
2.6412e+02
2.9157e+02
3.3056e+02
3.4089e+02
3.9573e+02
4.4029e+02
4.7583e+02
5.2827e+02
5.8404e+02
Lenght of x is: 39.8493
Lenght of y is: 1280.16
Distance(x, y) is: 1240.76
Correlation(x, y) is: 0.9887
A:
1.0000e+00 1.0000e+01 1.0000e+02
1.0000e+00 1.0556e+01 1.1142e+02
1.0000e+00 1.1111e+01 1.2346e+02
1.0000e+00 1.1667e+01 1.3611e+02
1.0000e+00 1.2222e+01 1.4938e+02
1.0000e+00 1.2778e+01 1.6327e+02
1.0000e+00 1.3333e+01 1.7778e+02
1.0000e+00 1.3889e+01 1.9290e+02
1.0000e+00 1.4444e+01 2.0864e+02
1.0000e+00 1.5000e+01 2.2500e+02
b:
5.8621e+02
-1.0156e+02
6.7586e+00
In [ ]: