What you should know about C¶
- Write, compile and run a simple program in C
- Static types
- Control flow especially
forloop - Using functions
- Using structs
- Pointers and arrays
- Function pointers
- Dynamic memory allocation
- Separate compilation and
make
Structs¶
Exercise 1
Write and use a struct to represent dates.
In [ ]:
Solution
In [ ]:
%%file ex1.c
#include <stdio.h>
typedef struct {
int day;
int month;
int year;
} date;
int main(int argc, char* argv[])
{
date d1;
d1.day = 29;
d1.month = 3;
d1.year = 2016;
date d2 = {30, 3, 2016};
date d3 = {.year = 2016, .month = 3, .day = 31};
printf("%d-%d-%d\n", d1.month, d1.day, d1.year);
printf("%d-%d-%d\n", d2.month, d2.day, d2.year);
printf("%d-%d-%d\n", d3.month, d3.day, d3.year);
}
In [ ]:
%%bash
gcc -std=c99 -o ex1 ex1.c
In [ ]:
%%bash
./ex1
Pointers¶
Exercise 2
Write and use pointers for working with
- doubles
- the date struct
- vector of doubles
- 2D array of doubles
In [ ]:
In [ ]:
In [ ]:
In [ ]:
Solution
In [ ]:
%%file ex2a.c
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char* argv[])
{
double x1 = 2.78;
double x2 = 3.14;
double *p1 = malloc(sizeof(double));
if (p1 == NULL) return -1;
double *p2 = calloc(sizeof(double), 1);
if (p2 == NULL) return -1;
printf("%p: %.2f\n", p1, *p1);
printf("%p: %.2f\n\n", p2, *p2);
p1 = &x1;
*p2 = x2;
printf("%p: %.2f\n", p1, *p1);
printf("%p: %.2f\n", p2, *p2);
// free(p1);
// free(p2);
}
In [ ]:
%%bash
gcc -std=c99 -o ex2a ex2a.c
In [ ]:
%%bash
./ex2a
Solution
In [ ]:
%%file ex2b.c
#include <stdio.h>
#include <stdlib.h>
typedef struct {
int day;
int month;
int year;
} date;
int main(int argc, char* argv[])
{
date *d1 = malloc(sizeof(date));
if (d1 == NULL) return -1;
d1->day = 29;
d1->month = 3;
d1->year = 2016;
printf("%d-%d-%d\n", d1->month, d1->day, d1->year);
printf("%d-%d-%d\n", (*d1).month, (*d1).day, (*d1).year);
free(d1);
}
In [ ]:
%%bash
gcc -std=c99 -o ex2b ex2b.c
In [ ]:
%%bash
./ex2b
Solution
In [ ]:
%%file ex2c.c
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char* argv[])
{
int n = atoi(argv[1]);
double *xs = calloc(sizeof(double), n);
if (xs == NULL) return -1;
for (int i=0; i<n; i++) {
xs[i] = i*i;
}
printf("%.2f\n", *(xs));
printf("%.2f\n", *(xs + 2));
printf("%.2f\n", xs[0]);
printf("%.2f\n", xs[2]);
free(xs);
}
In [ ]:
%%bash
gcc -std=c99 -o ex2c ex2c.c
In [ ]:
%%bash
./ex2c 10
Solution
In [ ]:
%%file ex2d.c
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char* argv[])
{
int rows = 2;;
int cols = 3;
double **xs = malloc(sizeof(double) * rows);
for (int i=0; i < rows; i++) {
xs[i] = calloc(sizeof(double), cols);
}
for (int i=0; i<rows; i++) {
for (int j=0; j<cols; j++) {
xs[i][j] = i+j;
}
}
printf("%.2f\n", xs[0][0]);
printf("%.2f\n", xs[1][2]);
for (int i=0; i<rows; i++) {
free(xs[i]);
}
free(xs);
}
In [ ]:
%%bash
gcc -std=c99 -o ex2d ex2d.c
In [ ]:
%%bash
./ex2d
Function pointers¶
Exercise 3
Write and use a function pointer.
Solution
In [ ]:
%%file ex3.c
#include <stdio.h>
#include <stdlib.h>
double add(double x, double y) {
return x + y;
}
double mult(double x, double y) {
return x * y;
}
int main(int argc, char* argv[])
{
double a = 3.0;
double b = 4.0;
double (*f)(double, double) = add;
typedef double (*fp)(double, double);
fp g = mult;
printf("%.2f\n", add(a, b));
printf("%.2f\n", f(a, b));
printf("%.2f\n", g(a, b));
}
In [ ]:
%%bash
gcc -std=c99 -o ex3 ex3.c
In [ ]:
%%bash
./ex3
Separate compilation¶
Exercise 4
Write header and implementation files for the add function, and use the function in a separate driver file. Use a makefile to compile the executable.
In [ ]:
Solution
In [ ]:
%%file ex4.h
#pragma once
double add(double x, double y);
In [ ]:
%%file ex4.c
#include "ex4.h"
double add(double x, double y) {
return x + y;
}
In [ ]:
%%file ex4_main.c
#include <stdio.h>
#include "ex4.h"
int main() {
double a = 3.0;
double b = 4.0;
printf("%.2f\n", add(a, b));
}
In [236]:
%%file makefile
ex4_main: ex4_main.c ex4.o
gcc -std=c99 -o ex4_main ex4_main.c ex4.o
ex4.o: ex4.c
gcc -std=c99 -c ex4.c
Overwriting makefile
In [237]:
%%bash
make
cc -c -o ex4.o ex4.c
cc ex4_main.c ex4.o -o ex4_main
In [238]:
%%bash
./ex4_main
7.00
In [234]:
%%file makefile
TARGET = ex4_main
OBJECTS = ex4.o
CFLAGS = -O3 -std=c99
LDLIBS = -lm
CC = gcc
all: $(TARGET)
clean:
rm $(TARGET) $(OBJECTS)
$(TARGET): $(OBJECTS)
Overwriting makefile
In [235]:
%%bash
make clean
make
rm ex4_main ex4.o
In [ ]:
%%bash
./ex4_main
What you should know about C++¶
- Anonymous functions
- Generalized function pointers
- Ranged for
- Using the standard template library
- Iterators
- Containers
- Algorithms
- The
randomlibrary - Using
amradillo
Exercise 5
Implement Newton’s method in 1D for root finding. Pass in the function and gradient as generalized function pointers. Use the method to find all roots of the polynomial equation \(f(x) = x^3 - 7x - 6\)
In [ ]:
Solution
In [266]:
%%file ex5.cpp
#include <iostream>
#include <vector>
#include <iomanip>
#include <cmath>
#include <functional>
using std::vector;
using std::cout;
using std::function;
using func = function<double(double)>;
double newton(double x, func f, func fprime, int max_iter=10) {
for (int i=0; i<max_iter; i++) {
x -= f(x)/fprime(x);
}
return x;
};
int main()
{
auto f = [](double x) { return pow(x, 3) - 7*x - 6; };
auto fprime = [](double x) { return 3.0*pow(x, 2) - 7; };
vector<double> x = {-5, 0, 5};
for (auto x_: x) {
cout << std::setw(2) << x_ << ": "
<< std::setw(3) << newton(x_, f, fprime) << "\n";
}
}
Overwriting ex5.cpp
In [267]:
%%bash
g++ -std=c++11 ex5.cpp -o ex5
In [268]:
%%bash
./ex5
-5: -2
0: -1
5: 3
Exercise 6
Use the armadillo library to
- Generate 10 x-coordinates linearly spaced between 10 and 15
- Generate 10 random y-values as \(y = 3x^2 - 7x + 2 + \epsilon\) where \(\epsilon \sim 10 N(0,1)\)
- Find the length of \(x\) and \(y\) and the Euclidean distance between \(x\) and \(y\)
- Find the correlation between \(x\) and \(y\)
- Solve the linear system to find a quadratic fit for this data
In [ ]:
Solution
In [ ]:
%%file ex6.cpp
#include <iostream>
#include <fstream>
#include <armadillo>
using std::cout;
using std::ofstream;
using namespace arma;
int main()
{
vec x = linspace<vec>(10.0,15.0,10);
vec eps = 10*randn<vec>(10);
vec y = 3*x%x - 7*x + 2 + eps;
cout << "x:\n" << x << "\n";
cout << "y:\n" << y << "\n";
cout << "Lenght of x is: " << norm(x) << "\n";
cout << "Lenght of y is: " << norm(y) << "\n";
cout << "Distance(x, y) is: " << norm(x-y) << "\n";
cout << "Correlation(x, y) is: " << cor(x, y) << "\n";
mat A = join_rows(ones<vec>(10), x);
A = join_rows(A, x%x);
cout << "A:\n" << A << "\n";
vec b = solve(A, y);
cout << "b:\n" << b << "\n";
ofstream fout1("x.txt");
x.print(fout1);
ofstream fout2("y.txt");
y.print(fout2);
ofstream fout3("b.txt");
b.print(fout3);
}
In [1]:
%%bash
g++ -std=c++11 ex6.cpp -o ex6 -larmadillo
In [2]:
%%bash
./ex6
x:
10.0000
10.5556
11.1111
11.6667
12.2222
12.7778
13.3333
13.8889
14.4444
15.0000
y:
2.4802e+02
2.6412e+02
2.9157e+02
3.3056e+02
3.4089e+02
3.9573e+02
4.4029e+02
4.7583e+02
5.2827e+02
5.8404e+02
Lenght of x is: 39.8493
Lenght of y is: 1280.16
Distance(x, y) is: 1240.76
Correlation(x, y) is: 0.9887
A:
1.0000e+00 1.0000e+01 1.0000e+02
1.0000e+00 1.0556e+01 1.1142e+02
1.0000e+00 1.1111e+01 1.2346e+02
1.0000e+00 1.1667e+01 1.3611e+02
1.0000e+00 1.2222e+01 1.4938e+02
1.0000e+00 1.2778e+01 1.6327e+02
1.0000e+00 1.3333e+01 1.7778e+02
1.0000e+00 1.3889e+01 1.9290e+02
1.0000e+00 1.4444e+01 2.0864e+02
1.0000e+00 1.5000e+01 2.2500e+02
b:
5.8621e+02
-1.0156e+02
6.7586e+00
In [3]:
x = np.loadtxt('x.txt')
y = np.loadtxt('y.txt')
b = np.loadtxt('b.txt')
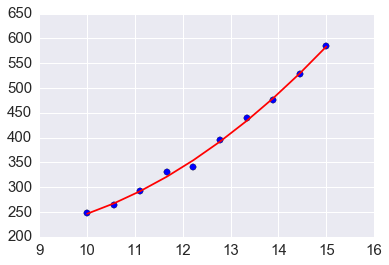
plt.scatter(x, y, s=40)
plt.plot(x, b[0] + b[1]*x + b[2]*x**2, c='red')
pass
In [ ]: