1
P_0 = ----- = $10
.10
2 1 .90
P_0 = ------- + ------- x --- = $10
1 + .10 1 + .10 .10
the same as before.
.50
P_0 = ----- = $5
.10
However, each original owner now has two shares of stock, his or her
wealth,
2 x P_0 = $10
will be unchanged.
Example 2
Suppose an all-equity firm has $2,000 cash flow residual (cash flow minus net investment). If the firm's value, including the $2,000 residual, is $42,000 and has 1,000 shares of stocks outstanding, consider two dividend policies of the firm:
$40,000
-------- = $39
1,025.64
so original shareholder's wealth is
$39 + $3 = $42
remains unchanged.
3. Summary of Factors That Could Affect Dividend Policy
Given that the firm's investment policy is fixed, MM show that the dividend policy is irrelevant. However, if capital market imperfections (e.g., taxes) are important or if dividend announcements signal new information, dividend policy will be relevant. In fact, there are important factors in dividend policy decision that are against high dividend payout and factors are in favor of high dividend payout and those that may affect dividend payout either way. A list of them is:
- Personal Taxes. (Dividends are taxed, but capital gains are deferred;
The latter tax rate used to be lower;
Since Tax Reform Act of 1986, equal treatment.)
- Transaction Costs (From reinvesting and firm's financing.)
- Tax Reasons (80% dividend exclusion rule; institutional investors)
- Legal and Institutional Reasons (e.g. `Prudent man' rule)
- Desire for Current Income
- Legal and Institutional Reasons (e.g. `Prudent man' rule)
- The Clientele Effect
- Information Content of Dividends
- Select Additional Capital Budgeting Projects
- Share Repurchase
- Acquire Other Companies
- Purchase Financial Assets
- Share Repurchase
4. Explanation of Factors
Personal Taxes
Before the Tax Reform Act of 1986, dividends and capital gains were taxed at different rates. Under the old laws, dividends were taxed as ordinary income (tax rate T_d of 50%) but you were only taxed on 40% of the capital gains (T_cg tax rate of 20%).
Under the old system, it seemed like individuals should prefer capital gains because T_cg < T_d. Second, you are not taxed on the capital gain until it is realized. So you can defer your taxation.
Under the Tax Reform Act of 1986 dividends and capital gains are treated symmetrically. Beginning in the 1988 tax year, the rate of taxation on both dividends and capital gains is a maximum of 28%. With the new legislation, it is more difficult to make the argument that corporations should not pay dividends because investors prefer capital gains.
One should also note that there are many large institutional investors that are tax exempt -- like pension funds. For these institutions, it is not even possible to tell a story about tax deferral. The institutions should be indifferent between a high dividend paying stock and a low dividend paying stock.
The only way to determine whether there is a tax effect makes dividend policy relevant is to empirically examine the data to see which group dominates the data. For example, Black and Scholes (1974) formed portfolios of stocks based on dividend payout ratios. Each of these portfolios was adjusted for risk with the Capital Asset Pricing Model. Black and Scholes wanted to see if there was any significant difference in total rates of return across portfolios that was related to dividend policy. There results showed that there was no significant difference. This implies that the market does not reward any particular dividend policy.
The bottom line on the tax issue depends on who the marginal investor is in the market. If the marginal investor is are large tax exempt institutions (which is likely to be the case), then they will eliminate any tax effect. If one stock is somehow rewarded for a particular dividend policy, the pension funds will buy in and drive the price up until that particular firm is no different from any other firm in the same risk class.
Transaction Costs
First, the investor must incur the transactions costs of reinvesting the dividend income. Second, the firm may have to pay for floatation costs (if dividend is financed by new equity) or some fees for borrowing.
Tax Reasons
The main item here is the fact that a large pool of investors are institutions which are tax-exempt.
The Clientele Effect
There are groups of individuals with different preferences for how they get the cash flows from the firm. Some shareholders may prefer stocks that do not pay dividends. Other shareholders may prefer stocks that pay a regular dividend. Although we have seen how people can construct their own dividend policy, there are some that "prefer" -- for whatever reason -- a certain type of dividend policy.
Investors will form their well-diversified portfolios of stocks to have the desired dividend policy. In equilibrium, no firm can affect its value by changing its dividend policy. If a firm did change the policy, it would be dropped by one clientele and picked up by another. Clearly, one clientele is as good as another. All clienteles would prefer not to be constantly rebalancing their portfolios as firm switch policies. Rebalancing is expensive due to transactions costs. Hence, all investors transactions costs are minimized if the firm maintains a stable dividend policy.
Information Content of Dividends
There may be information content to dividends. The dividend may be a signal to the public of the management's anticipations for future policy of the firm and prospects. If there is new good information, then managers may signal this information to the public by raising dividends. There is a reluctance to lower dividends because managers want the dividends to represent expectations of the future value of the firm.
An obvious question is why don't the managers inform the public about new prospects by press releases or other non-dividend related methods? In fact, the managers do make use of the press to announce new prospects. The problem is credibility. Why should the public believe them? Furthermore, there is an obvious bias because it is unlikely that they will phone a reporter to tell them bad news. The dividend is a more credible means of conveying information because it is costly to the firm. The more costly the signal the more believable it is.
5. Capital Structure: An Introduction
There are many methods for the firm to raise its required funds. But the most basic and important instruments are stocks or bonds. The firm's mix of different securities is known as its capital structure. A natural question arises: What is the optimal debt-equity ratio? For example, if you need $100 million for a project, should all this money be raised by issuing stocks, or 50% of stocks and 50% of bonds (debt-equity ratio equals 1), or some other ratios? Modigliani and Miller (MM) showed that the financing decision doesn't matter in perfect capital markets. Their famous Proposition I states that the total value of a firm is the same with whatever debt-equity ratio (assuming no taxes). If this is true, the basic exercise in capital budgeting (in Bond Valuation) can be directly applied to project evaluation for firms with different debt-equity ratios. Remember that we have implicitly assumed firms are all-equity financed in previous lectures. However, in practice, capital structure does matter. Then why do we bother to learn the MM's theory? This theory is valid under certain conditions. If the theory is far from true, so are the conditions. An understanding of the MM's theory helps us to understand those conditions, which, in turn, helps us to understand why a particular capital structure is better than another. In addition, the theory tells us what kinds of market imperfection we need to look for and pay attention to. The imperfections that are most likely to make a difference are taxes, the costs of bankruptcy and the costs of writing and enforcing complicated debt contracts.
6. MM Proposition I and Proposition II: No Tax Scenario
MM Proposition I concerns about the irrelevancy of the value to capital structure. Notice that in what follows financial instruments are assumed to take only two forms: stocks and bonds. In this set up, the value of a firm is defined as:
V = B + SwhereB is the market value of the firm's debt and S is the market value of the firm's equity.
Example 1
Suppose a firm has $10 million debt and 5 million shares of stock. Assume the stock sells at a market price of $20, then
V = 10,000,000 + (5,000,000 x 20) = $110,000,000
To obtain MM Proposition I, we make assumptions:
- Homogeneous expectations
- Homogeneous business risk
- Perpetual cash flows
- Perfect capital market
- Perfect competition (every one is a price taker)
- Firms and investors can borrow and lend at the same rate
- Equal access to all relevant information
- No transaction cost (taxes or bankruptcy costs)
- Firms and investors can borrow and lend at the same rate
- Homogeneous business risk
MM Proposition I
The value of the levered firm, V_L, must be equal to the the value of the unlevered firm, V_U.
Example 2
Suppose a firm earns $100 in perpetuity. It is all-equity with 100 shares of stock. If each sells for $10, the value
V_U = 100 x $10 = $1,000
Now assume the CEO suddenly decided the firm should issue $500 dollars of debt. The equilibrium price of the stock will drop to $5 per share and so the value of the levered firm:
V_L = 500 + (100 x 5) = $1,000the same as before.
Why should the stock price drop to $5 per share? To understand it, suppose you own one share of the stock.
Case 1. Unlevered:
Assume the firm pays $1 dividends in perpetuity and the interest rate is 10%. You are willing to pay $10 for the stock because
1
P_0 = ------ = $10
.10
Case 2. Levered:
After leverage, the firm has to pay interest, $50 =500 x 10%, on the $500 debt each period. So it can only pay $.50 dividends in perpetuity. As a result, the price for the stock is
.50
P_0 = ------ = $5
.10
Assume the debt money
was distributed to you today from the CEO, that is
$5 per share, then you still have in total $10.
So, for you, as a shareholder, you don't care
what capital structure the firm has.
Proof of the MM Proposition I
Assume two firms are identical except for the capital structure. One firm has no debt, with value V_U=S_U, while the other does have debt, with value V_L=B_L+S_L. Since the two firms are identical, they generate the same cash flows in the future. So, if you either buy the unlevered firm or buy the levered firm, you will get the same cash flows. By the law of one price, both firms must sell at the same price. What do you pay for the unlevered firm? $S_U$. What do you pay for the levered firm? $B_L + S_L$. Therefore
V_L = V_UMM Proposition I says the debt-equity ratio doesn't matter to the value of the firm. As an investor, you are concerned about the expected return on your money, so you ask: what happens to the stock's expected return under different debt-equity ratios?
To answer the above question, let us define R_0 as the cost of capital to a firm, or the overall required rate of return:
Expected earnings to be paid to investors
R_0 = -----------------------------------------
Value of the firm
Example 3
If Intel is expected to earn $1 billion next year and its value is $12 billion.
1
R_0 = ---- = 0.0833
12
Now let
- B = the market value of the firm's debt
- S = the market value of the firm's equity
- R_B = the interest rate, or cost of debt
- R_S = the expected return on equity, or the cost of equity
- S = the market value of the firm's equity
Then the expected earnings to be paid to all investors:
Expected earnings = To bondholders + To Shareholders
B x R_B + S x R_S
Dividing S+B on both sides we get:
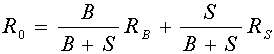
Solving for R_S we have the MM Proposition
MM Proposition II
The expected turn on equity is a linear function of the debt-equity ratio in the form:
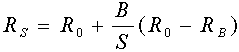
Notice that, by MM proposition I, R_0 stays constant with different capital structures. In particular, it represents the expected return when the company is all-equity financed. Since the expected return on risky assets is generally greater than the riskless rate, we know R_0 > R_B is generally true as well. Thus, MM Proposition II implies that, in general, the higher the debt-equity ratio, the higher the the expected turn on equity.
7. MM Proposition I and Proposition II: With Corporate Taxes
In the real world, corporations are taxed at rates as high as 34%. However, there is a quirk in the tax code that only those earnings after interest payments are taxable. This is one of the most important reasons for firms to use debt financing. To understand it, let us first examine Example 2 with a tax rate of 34%
Example 4
Case 1. Unlevered:
The earnings after taxes is $66, so the firm can pay only $0.66 dividends in perpetuity.
.66
P_0 = ----- = $6.6 V_U = 100 x 6.6 = $660
.10
Case 2. Levered:
After leverage, the firm has after interest payments earnings of $50 each period. Then, after paying taxes, it can pay $0.33 dividends in perpetuity. So
.33
P_0 = ----- = $3.3 V_L = 500 + (100 x 3.3) = $830
.10
Notice that the value with leverage
has increased from $660 to $830.
Where does the extra amount, $170=$830-$660, come from?
Intuitively, the value of the firm is a pie.
It is sliced between the owners of the firm (shareholders
and bondholder, if any) and the government.
In the unlevered case, the government takes 34% away.
But in the levered, only 50% of the pie is taxable
and so the government effectively takes only 17%.
The total pie is the present value of the earnings, $1000.
So the government takes 17%x$1000=$170 less
in the levered case than in the unlevered case. This amount adds to
the value that the owners of the firm can enjoy:
V_L = 830 = 660 + 170 = V_U + 170 = V_U + (34% x 500)where the tax shield is the tax rate multiplied by the present value of the dollar interest payments.
In general, we have:
MM Proposition I (with corporate taxes)
The value of the levered firm is:

and the value of the unlevered firm is computed from the formula:
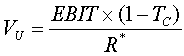
where T_C is the corporate tax rate; EBIT is the expected earnings before interest and taxes; and R* is the discount rate for an all-equity firm (after tax).
Proof of the MM Proposition I
For the unlevered firm:
the earnings after the corporate taxes are:
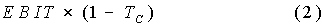
For the unlevered firm the taxable income is earnings minus interest payments, EBIT - (R_B x B), and so the earnings after interest payments and taxes are:

The present value of the cash flow (2) gives V_U and that of (3) gives V_L. Together they give (1).
With a proof similar to the one we gave earlier, we can show:
MM Proposition II (with corporate taxes)
The expected return on equity is a linear function of the debt-equity ratio in the form:

Notice that (1) and (4) include the no-tax case MM Propositions as special cases. This is because, in the no-tax case, the discount rate R* is R_0 and T_C=0.
8. Implications of the MM Theory
The market value of a levered firm equals the market value of an unlevered firm plus the present value of interest tax shields. In order to get the simple expression above, we have assumed that the debt is perpetual. More generally, the tax shield term would be the present value of the interest tax shields.
The implication of the model with corporate taxes is that the value of the firm is maximized when it is financed entirely by debt. This is not a very attractive implication for the model. Clearly, no firm is financed 100% by debt. There are a number of real world constraints that need to be considered. First, there are institutional and legal restrictions (some institutions will not purchase stock of a firm that has a debt--equity ratio that exceeds some cutoff). Second, there are costs imposed for going bankrupt that might persuade the firm's management not to increase the debt--equity ratio too high. Third, the interest tax shield may exhaust taxable income (this suggests an upper bound on the amount of debt). Finally, there may be conflicts of interest between stockholders and bondholders.
Each of these points suggests that the 100% debt policy may not be optimal for a firm. If we look to the market, the average debt to value ratio is less than 40%. Furthermore, a survey of 768 of the largest industrial firms shows that 126 (16%) have no debt in their capital structures. This empirical evidence suggests that the 100% debt policy is clearly not what is observed. The wide range of debt--equity ratios in the market could indicate that the original proposition about the irrelevance of the capital structure may have more merit than we initially gave it.
Bankruptcy Costs
There are many costs involved in bankruptcy. The direct costs are legal fees and court costs. The indirect costs arise from discontinued operations, the hesitancy of customers to purchase the product and the unwillingness of suppliers to extend any credit. These costs make it unlikely that a firm will push its debt equity ratio very high. If we take the bankruptcy costs into account, then there may be an optimal capital structure where the marginal tax advantage equals the marginal bankruptcy costs. Note that the marginal bankruptcy costs may be different across firms. This may explain why all firms do not have the same level of debt--equity.
Exhausting the Benefits
Obviously, if the firm is unlikely to earn taxable profits, the effective tax shield is small. As a result, it should not borrow.
Conflicts of Interest
Once the debt is outstanding, shareholders have the incentive to take actions that benefit themselves at the expense of the bondholders. So if there is debt outstanding, the objectives of maximizing the value of the firm and the value of the equity are not identical. Some examples of bondholder--shareholder conflicts are: claim dilution, dividend payout and asset substitution. Let's examine in more detail some of these conflicts.
Consider claim dilution. With debt outstanding, stockholders have incentives to issue claims of equal or senior priority. The proceeds from the "new" debt issue will be greater the higher the priority of the new debt. The claim dilution increases the risk of the "old" debt and its market value falls. The combined value of the new and old debt is fixed. By making new debt equal or higher priority, the value of the old debt falls and the proceeds from the new debt issue rises. Claim dilution benefits the stockholders at the expense of the "old" bondholders.
But the bondholders are not stupid. The price of the bonds equals the present value of the expected cash flows. The bondholders include the affects of conflicts of interest in estimating cash flows and pricing the debt. Bondholders only pay for what they expect to get.
Since the conflicts of interest between stockholders and bondholders reduce the price of the debt, the stockholders bear all of the costs of the conflict. Even though the shareholders bear the costs of the conflict, there is still an incentive to extract value or expropriate from the bondholders -- after the debt is outstanding.
Since the stockholders bear the costs that arise from the conflicts of interest, they have an incentive to minimize the agency costs. Bond covenants are detailed enforceable contracts that reduce agency costs by restricting the stockholders' actions after the debt is issued. The covenants may restrict the production and investment policy (i.e. mergers, sale of certain assets and lines of business). The covenants may restrict the financial policy of the firm (i.e. dividend payouts, priority and total debt). Furthermore, there is usually a provision for auditing. The bond covenants will reduce but will not eliminate these agency costs. Note that there are also costs involved in monitoring the firm's actions.
9. Capital Structure as Options
I mentioned that both the debt and the equity of the firm could be considered options. Let's explore this idea in some more detail. The bondholders are promised payments of $A next period. If default occurs, then the bondholders own the firm. The stockholders receive all residual cash flows after the payments to bondholders. Consider the distribution of the value of the firm.

Now consider the payoff schedule. Suppose the debt has time to maturity, T. The standard deviation of the firm's value is STD.
Payments to V <= A V > A Position
Stockholders 0 V - A c(A,T,STD) Bondholders V A V - c(A,T,STD)
Total V V V
Note that c(A,T,STD) is a call option. The call option is a function of the exercise price, A, the time to maturity, T, and the standard deviation of the return on the underlying asset, STD. The payments to the stockholders and bondholders add up to the total cash flows of the firm.
Consider the position diagrams. The position diagram for the call option is straightforward.

Note that V represents the value of the firm at the expiration or final payment of the principal on the debt. This diagram indicates that the stockholders have a call option on the value of the firm. The payoff is determined by Max[0, V-A].
The position diagram for bondholders is slightly more complicated.

The bondholders hold the value of the firm and write a call option (the shareholders buy it in the form of common equity). Combining the payoffs of the long position in the value of the firm with a short position in the call delivers the above diagram. The payoff stream is Min[V, A].
Acknowledgement
Some of the material for this lecture is drawn from Richard Ruback's note, "Dividend Policy" and Michael Hemler's note "Corporate Finance."

BA 350 Index
Page
Campbell
Harvey's Home Page