Copyright 1995 Campbell R. Harvey. All rights reserved.
A theory's success if often judged by its out-of-sample performance. In my dissertation at the University of Chicago in 1986, I argued that the term structure of interest rates could be used to forecast economic growth. While the evidence was impressive (almost 50% of the variance in real GNP growth could be explained and the forecasts were not beaten by any commercially available projections), the model was 'fit' on historical data. Since the writing of the paper, we have experienced a complete business cycle. Now, we can perform a post-mortem on the out-of-sample performance.
I will show that the term structure model provided accurate and timely forecasts of the most recent business cycle. The model predicted a downturn five quarters before the recession officially began. The model forecast the duration of the recession to be three quarters which is now considered the official length. Furthermore, I will argue that the term structure provided the correct signal in early 1995 when the interest rate curve flattened.
Consider a simple example. Assume that investors want to insure their economic well being. Most would prefer a reasonably stable level of income rather than very high income in one stage of the business cycle and very low income in another stage. This pre ference for stability drives the demand for insurance or hedging.
Suppose the economy is presently in a growth stage and the general consensus is for a slowdown or recession during the next year. This desire to hedge will lead consumers to purchase a financial instrument that will deliver payoffs in the slowdown. Such a n instrument is a one year discount bond.
If many people are buying the one-year bond, the price of the security will increase and the yield to maturity will decrease. To finance the purchase of the one year bonds, consumers may sell their shorter term assets. This selling pressure will drive down the price of the short term instrument, and as a result, raise its yield.
So, if a recession is expected, we will see long rates decrease and short rates will increase. As a result, the term structure or yield curve (difference between long rates and short rates) will become flat or inverted. The shape of the term structure o f interest rates today provides a forecast of future economic growth.
From this example, it should be clear that the interest rate based model is very simple. It contains only two components. The first component is the slope of the term structure or the long term--short term yield spread. The second component is a measure o f the average propensity to hedge in the economy (which is provided in my 1989 paper and in my 1986 dissertation).
The previous interpretation relied on the actions of consumers and investors. There is a production side explanation which is equivalent. Suppose the corporation expects a downturn in the longer horizon. Capital projects are less attractive because cash f lows are usually positively correlated with the business cycle. Hence, projects are delayed. Given that corporations often try to match the maturity of the financing of a project to the life of a project, this will reduce the pressure on the corporate bo nd market (i.e. less long term corporate bonds being floated). This will tend to reduce long-term interest rates. If, at the same time, corporations concentrate on shorter maturity projects and shorter maturity financing, the shorter term rates will have positive pressure. These two effects together, or separately, will reduce the slope of the yield curve.
In previous research, I have shown that more elaborate (and expensive) econometric models are unable to deliver predictions that outperform the simple term structure model. I have tested this model on the U.S. economy and the other G-7 countries.
Recessionary periods are classified by the National Bureau of Economic Research (NBER). A recession is the period between an economic trough and peak. The NBER Business Cycle Dating Committee decided the most recent recession began in July 1990 (peak) an d ended March 1991 (trough) -- a duration of about three quarters.
Consider the record of the term structure over the past 25 years:
Recession 90Q3-91Q1 [Total GDP decline 1.8%]: Term structure inverts in three consecutive quarters 89Q2-89Q4 providing a five quarter lead.
The recent inversion in 89Q2-89Q4 was mild compared to other inversions. For example, in 89Q3 the magnitude of the inversion was about 30 basis points (long-term rates .3% below short-term rates). In contrast, the inversion in 80Q4 was 340 basis points or 3.4%.
The magnitude of the inversions reveals the severity of the recession. The term structure forecast in late 1980 predicted a serious recession beginning in mid-1981. This forecast turned out to be accurate.
Based on the inversion in the summer of 1989, I forecasted reduced economic growth. However, the mild inversion indicated that the recession would not be a serious as the previous three episodes. My model also correctly predicted the end of the recession. To quote the late Leonard Silk, (New York Times July 20, 1990), "the Harvey model ... now predicts that ... the economy is likely to be sluggish until mid-1991 and then turn gradually upward.''
Overall, the model delivered a five-quarter advance signal of the downturn in July 1990. In addition, the model also caught the upturn. The recession lasted three quarters and the term structure inversion also lasted three quarters. The model also predict ed that the downturn would be less severe than the three previous episodes. All of these predictions have been validated out of sample.
In early 1995, the term structure came very close to inverting. In Business Week January 16, 1995 I am quoted as saying that "inverted yield curves are clear omens of recession." However, given that the curve had not inverted, "Harvey is countin g on only a slight moderation in the growth rate" for 1995. This forecast has held so far. We have experienced slower growth in 1995 - but there is no evidence of a recession.
The updated regression equation estimation (using Gross Domestic Product rather than GNP which was reported in my 1989 article) shows that the explanatory power is still highly significant with the most recent data. The basic forecasting equation is
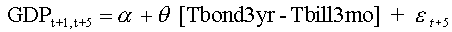
Using the spread between the three year yield to maturity and the 90-day Treasury bill, the explanatory power over the 1960:1-1995:1 period is 30% (with an alpha of 2.077 and a theta of 1.390). Over the 1970:1-1995:1 period, the explanatory power is is 47 % (with an alpha of 1.48 and a theta of 1.55). Over the 1980:1-1995:1 period, the model R-square is 48% (with an alpha of 1.446 and a theta of 1.321).
Below we can visualize the performance of the term structure model.

As with any model, the term structure does not perfectly forecast economic growth. Although, the model correctly predicted the most recent turning point, the forecasts of economic growth were higher than the realized growth.
A number of simplifying steps have been taken in developing the model. The intercept, alpha, is assumed to contain the volatility of both the business cycle and the spread. If there is time-varying volatility, then the intercept should be adjusted.
In the theoretical development of the model, the real business-cycle is matched with the term structure of real interest rates. These real rates are not available. I assume that the spread between nominal rates is approximately equal to the spread between real rates.
This involves two levels of inflation assumptions. First, the expected real rate is assumed to be the difference between nominal rates and expected inflation. This is the so-called 'Fisher effect'. It is not necessarily true. A risk premium may be wedged between the expected real rate and the nominal rate deflated by the expected inflation.
Second, I assume that the term structure of expected inflation is flat. That is, the expected annualized inflation component for the 3 month Treasury bill is identical to the annualized inflation part of the 3 year bond.
This assumption could potentially account for some of the model errors. Indeed, one could argue that the term structure of expected inflation has been positively sloped for the last two years. The CPI rose only 2.6% in 1992. Given the long-term bonds are still yielding more than 7%, most believe that expected long-term inflation exceeds expected short-term inflation.
A positive term structure of inflation could account for why the term structure inversion in the summer of 1989 was so mild and the steep upward slope since then. Incorporating the term structure of inflation could lead to an improved forecasts.
There are a number of promising directions for further research. I have published a number of international extensions of my work. In some countries, the term structure has remarkable ability to track GDP growth. In other countries, the evidence is not as convincing. Interestingly, the difference between the local term structure of interest rates in a particular country and the U.S. term structure, has the ability to forecast the part of economic growth which is not related to "world" economic growth, i.e. the idiosyncratic country real economic growth.
The following visualizations are available:
Canada.
Germany.
UK.
France.
Italy.
Japan.