|
Visualization, Graphics
& Samplers
VISION, the highest informaion bandwidth channel of human perception and cognition. Turning numbers into images.
Notes on the RGB Color Cube & Color Space
Deconstructing a Bitmap (.bmp) Image File |
|
|
3D Color Cube to Ramps: colorRamp() and grayRamp() Functions
Color is defined as a 3D cube with 3 dimensions along 3 axes: red, green and blue. The numerical values along each axis range from 0 - 255 corresponding to a standard 8-bit byte. Consequently, if we have a set of data ranging from 0 to some number, we can pick a color from the cube to represent that number.
The minimum value is not passed in the function call. It is set to 0. It maps to BLACK.
The varying value, part, is the first parameter in the function call. It maps somewhere in between.
The maximum value, whole, is the second parameter in the function call. It maps to WHITE.
The colorRamp(part, whole) and grayRamp(part, whole) function calls return colors in proportion to the two parameters given. For example, colorRamp(121, 242) will return a color half-way down the color spectrum, colorRamp(4444, 6666) will return a color two-thirds down the color spectrum.
The source code contains the latest version of the ramp functions. Other applications may contain older versions which which may not work as well.
|
|
Color
Cube Cutout
Generates an image of an unfolded color cube which
can be cut out and assembled into a 3d object. The color cube is the key
to rendering colors on a computer screen. Every color that can be displayed
is somewhere in or on the cube. It
has three axes: red, green and blue (RGB), also called the additive primary
colors. Zero values for each of the RGB additive primaries define the black corner.
Full values (255) for each of the RGB additive primaries define the white corner
at the opposite end of the cube. The additive primaries, red, green and blue, are at the three
corners nearest black. The subtractive primaries, magenta, yellow and cyan,
are at the three corners nearest white. All the fully saturated colors
are located on the surface of the cube. On the diagonal axis stretching
from black to white inside the cube are all the shades of gray. Near this
axis towards the white end are the light pastel colors, and towards the
black end are the browns.
|
|
XE6 String Art with colorRamp(part/whole)
This algorithm replicates the "string art" that was popular in the 1960s. The PaintBox is 500 by 500 pixels and the routine stretches a string (draws a line) from one point to another around the periphery of the square. Beginning one pixel to the right of the top-left corner, it draws a line to one pixel down from the top-right corner, to one pixel to the left of the bottom-right corner, to one pixel up from the bottom-left corner. Then it does the same for two pixels distance, then three, then four, etc. always moving in a clockwise direction. With the "loop interval" set to 1 it does this 500 times. The interval may be changed as well as the speed ("delay"). Each journey around four sides counts as an iteration. Each iteration may be colored differently using the colorRamp() function.
The function is called with "colorRamp(part, whole)" in which "part/whole" is the fractional part of the entire spectrum. If the value of "whole" is set to the number of "iterations," a complete color spectrum is generated. If "whole" is much greater than "iterations" only a truncated spectrum is generated. If "whole" is much less than "iterations" the spectrum repeats several times.
|
|
Cheshire Cat - A Borderless Transparent Window (Form) and Image
You can easily get away from the normal Windows "look" by setting Form1->BorderStyle = bsNone, setting Form1->Color = clBlack, Form1->TransparentColor = true and Form1->TransparentColorValue = clBlack. With no border, we have no way to close or drag the form, so we need to create a user interface to fire those events. The color is, after all, your choice, but remember everything that you put on the form that is black will be transparent. Now the entire form has no border and is transparent, and thus entirely invisible. So now we need to put something visible on it.
I decided to use a transparent bitmap image as the user interface. I selected the Cheshire cat image, selected all the background area in PhotoShop, and penciled it in uniformly in absolute black. Remember that the lower left pixel is the "key" that is used to identify the transparent color in Borland. I put a TImage component on the Form, AutoSized it, and set Transparent = true. Instead of buttons, I placed TShape objects over the cat's eyes, ears and belly. The BrushStyle and PenStyle properties of those TShapes wer set to bsClear and psClear. A MouseDown event on the left eye changes the color of the form to Aqua, a non-transparent color. Mousing down on the right eye restores the form color to Black. Similarly, a MouseDown event on the left ear reveals the TShapes over the two eyes by changing the eye TShap Brush and Pen Styles to bsSolid and psSolid. Mousing down on the right ear restores the style clear settings. A MouseOver on the TShape over the belly initiates a jiggle. A left button MouseDown on the cat image initiates a drag and a right button MouseDown on the cat closes the application. Sounds have also been added to these events, but the sounds are likelly not to be available to any but the machines installed in Duke, Classroom #6.
Interestingly, Alt/PrintScrn captures the application but with a black background. A simple PrintScrn captures the entire display and the transparency is preserved.
|
 |
Main and Popup Menus
An introductory demonstration of:
TMainMenu, TPopupMenu and TImageList.
|
|
Movable Spotlight
This enables the user to treat the data projector as a movable spotlight. A MouseDown and drag will move the spot. Rolling the MouseWheel will change the spot size. The application also demonstrates the use of the MouseWheel to change the Position of the TrackBar. Since the TrackBar is the only object that receives Focus in this application, there is no need to call TrackBar->SetFocus(). Since there is no need for the user to see the TrackBar, its size (Height and Width) have been set to zero. Setting the TrackBar->Visible property to false will NOT accomplish this.
|
|
|
Radians
This illustrates the relationship between trigonometric
functions computing radians and their mapping to the screen. The black
numbers are a plot of positions computed from -10 radians to + 10 radians.
The red numbers are a plot of radians
computed from those positions. Notice that the plots are not entirely
reciprocal. Also note that the function
atan1(dy, dx) returns the direction in the correct quadrant.
|
|
|
Line Art
This sampler illustrates some simple algorithmic line
drawings. "Spiral" and "Lattice" are drawn by an agent
which can move Up, Down, Left and Right. "String" is drawn from
point to point in any direction. Some of these patterns appear in the
decorative arts of several cultures. Although the algorithms used in this
application are computationally efficient for PCs, they may NOT be the
most efficient algorithms used by the peoples of those cultures since
human and PC computational hardware systems differ.
|
|
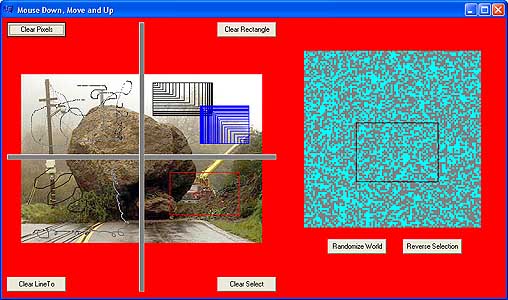
This sampler experiments
with event handlers in order to create code that functions as a selection
box. The two mouse buttons function differently. |
Mouse Down, Move and Up
- The UL box uses the Canvas->Pixels
call.
- The LL box uses the Canvas->LineTo
call.
- The UR box uses the Canvas->Rectangle
call without calling Refresh().
- The LR box uses the Canvas->Rectangle
call as well as Refresh().
- All Clear buttons call Refresh()
which clears the Canvas but not Images.
The Game-Of-Life screen clears the
Canvas but redraws it every time the selection box changes size (using
the OnPaint event-handler).
Pressing Reverse Selection changes the selected cells.
|
|
|
intraSTELLAr
In homage of Frank Stella's 23 algorithmic squares
(1974).
Makes use of a user-written array of TShapes.
Seperate events are fired for each square's mouse-over
and transfers TShapeMouseMove to FormMouseMove..
|
|
|
Alena's Tree
Adapted from Gary Flake's Jave implementations of L-Systems,
Alena's Tree builds several classes of trees with colors mapped to the
depth of the rules. This application appears to require the ability to
write to and read from a text file of its own creation which must be located
in the same folder as the application.
|
|
|
Red-Shift
A foundation of shrinking color-changing TShapes...
Makes use of a user-written array of TShapes
and transfers TShapeMouseMove to FormMouseMove..
|
|
|
Grid
A foundation of shifting brush and pen widths and colors
as well as TShapes square sizes. Everything depends upon the distance
from the cursor position. Makes
use of a user-written array of TShapes and transfers TShapeMouseMove to
FormMouseMove. The timer is introduced to change the coloring algorithm
every few seconds.
|
|
|
Shapes
An array of shapes is created in random positions,
sizes, brush and pen widths. Colors are randomly selected from the color
cube in one of three ways: along the edges only, on the faces (surfaces)
only, or from anywhere within the volume of the cube. The jiggle button
moves the shapes at random. See what other interesting behaviors you can
generate with mouse-over events or other algorithms.
Makes use of a user-written array of TShapes.
|
|
|
Botticelli
An example of how you might dynamically alter a .bmp
image. In this instance, the red, green and blue values are either incremented
or decremented by one at each rendering. After 256 renderings the image
returns to its original appearance. See the Realworld
Interfaces page for a more complex example.
BMP Images.
|
|
|
Time Use
A prototype for timer to record the beginning and
ending of six activities occurring simultaneously. The present version
only produces a running visualization. File output will be added and a
version rewritten for the PocketPC.
|
|
|
Color
Scale and Pseudo Elevations
When we wish to visualize numbers, like colors representing
elevations on a topographic map, we need to devise an appropriate mapping
between a number and a color. One simple way to do this is to define a
path along the color cube from black to white. This is called a color
ramp. We know the length of the path and so we can scale the number along
that length. This program illustrates a color ramp from black to white
that is actually a path along the edges of the color cube. See if you
can follow that path along the edges of the color cube you have assembled.
Are there other paths that might lead to a more aesthetic or "natural"
color scale?
|
|
|
Graphics Sampler
This sampler introduces some basic graphics commands
and objects as well as rudimentary algorithms through the use of single
and nested for loops.
|
|
|
Circles
This uses the Ellipse(x1,
y1, x2, y2); command to draw a progression of circles using
a for loop. Larger
drawings always obliterate what they overlap, so changing the order in
which the circles are drawn yields different results. Interesting Moire
fringes appear when the lines are drawn close together. The circles are
colored using the colorRamp()
function.
|
|
|
Ziegler Components
Components are pre-written programs that function
as drag-and-drop objects making our task of writing applications much
easier. This sampler shows some of the more useful panels, knobs, dials,
meters, gages and charts that were donated by Claus Ziegler from Denmark.
|
|
|
Parallelizing a Cellular World:
Checking Nieghborhoods
Checking the neighborhood of a cell in a cellular
world can be a confusing process. This application graphically shows how
an immediate neighborhood (which may contain invalid cells that
are out of bounds) can be used to build a wrapped neighborhood
(which contains only valid cells). This is a donut shaped world or technically
a torus. It has no edges and agents cannot fall off.
|
|
|
File Input and Output: Open and
Save
This program shows how to use the Save and Open Dialog
Components to write numbers to and read numbers from a file. When you
press "Compute," the squares, cubes, sines and cosines of the
numbers from 0 to 9 will be calculated. When you press "Save,"
the results will be written to a file. When you press "Open,"
the results will be read from a file and rendered to the Canvas. The final
screen cannot be rendered if the file has not been written to and read.
Once you have created the file, examine its format in both a text and
binary editor and see how it corresponds to the source code. Numbers are
separated by blanks (SP). Sets of numbers are separated by the end-of-line
mark (EOL) which is actually a carraige return (CR) and a line feed (LF).
|
|
|
Mika's Planets
Mika's program
uses the Ellipse( ) function and Labels with changing Visible properties
to present a sequence of circles and text (planets) on the screen. Timing
is controlled by counting the iterations in a for ( ) loop and using if(
) statements to switch visibility from false to true.
|
|
|
Using ListView to Edit an Array
In this application,
an array of 400 random values is created when the program starts. The
array values are displayed in a ListView component along with the index
for each value. The values may be edited by clicking momentarily on each.
"Try" and "catch" are used to allow the user from
recovering from any errors, such as entering letters instead of numbers.
|
|
|
Trackbar and Dial
Just an example of how to input values into a program.
|
C++ Builder - Visualization, Graphics & Samplers
