
Often a time series which has a strong seasonal pattern is not satisfactorily stationarized by a seasonal difference alone, and hence the seasonal random walk model (which predicts the seasonal difference to be constant) will not give a good fit. For example, the seasonal difference of the deflated auto sales series looks more like a random walk than a stationary noise pattern. However, if we look at the first difference of the seasonal difference of deflated auto sales, we see a pattern that looks more-or-less like stationary noise with a mean value of zero:
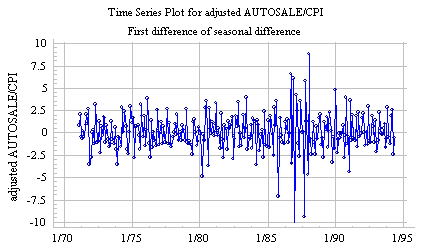
(Even if the mean value of a twice-differenced series is not exactly zero, we normally assume it is zero for forecasting purposes: otherwise we would be assuming a trend-in-the-trend, which would be dangerous to extrapolate very far.)
For monthly data, whose seasonal period is 12, the first difference of the seasonal difference at period t is (Y(t) - Y(t-12)) - (Y(t-1) - Y(t-13). Applying the zero-mean forecasting model to this series yields the equation:
Rearranging terms to put Y(t) by itself on the left, we obtain:
For example, if it is now September '96 and we are using this equation to predict the value of Y in October '96, we would compute:
In other words, October's forecast equals September's value plus the September-to-October change observed last year. Equivalently, we can rewrite this as:
which says that October's forecast equals last October's value plus the year-to-year change we observed last month. (These preceding two equations are mathematically identical: we've just rearranged terms on the right-hand-side.)
This forecasting model will be called the seasonal random trend model, because it assumes that the seasonal trend (difference) observed this month is a random step away from the trend that was observed last month, where the steps are assumed to have mean zero. To see this, rewrite the equation in terms of seasonal differences:
In other words, the expected seasonal difference this month is the same as the seasonal difference observed last month. Now compare this behavior with that of the seasonal random walk model: the seasonal random walk model assumes that the expected values of all future seasonal differences are equal to the average seasonal difference calculated over the whole history of the time series. In contrast, the seasonal random trend model assumes that the expected values of all future seasonal differences are equal to the most recently observed seasonal difference. Moreover, the seasonal random trend model assumes that the actual seasonal differences will be undergoing a zero-growth random walk--rather than fluctuating around some constant mean value--so their values will become very uncertain in the distant future.
The seasonal random walk model and the seasonal random trend model both predict that next year's seasonal cycle will have exactly the same shape (i.e., the same relative month-to-month changes) as this year's seasonal cycle. The difference between them is in their trend projections: the seasonal random walk model assumes that the future trend will equal the average year-to-year trend observed in the past, whereas the seasonal random trend model assumes that the future trend will equal the most recent year-to-year trend.
Returning to our example, if our last recorded value was for September '96, the seasonal random trend model will predict October's value to satisfy Y(Oct'96) - Y(Oct'95) = Y(Sep'96) - Y(Sep'95). If we then bootstrap the model one month into the future to predict November's value, the model will predict that Y(Nov'96) - Y(Nov'95) = Y(Oct'96) - Y(Oct'95) ...but this is exactly equal to Y(Sep'96) - Y(Sep'95) again, because the October '96 forecast must be used in place of an actual value. Thus, all future seasonal differences, as predicted from time origin September '96, will be identical to the September-to-September difference.
The seasonal random trend model is a special case of an ARIMA model in which there is one order of non-seasonal differencing, one order of seasonal differencing, and no constant or other parameters--i.e., an "ARIMA(0,1,0)x(0,1,0) model." In Statgraphics, you would specify a seasonal random trend model by choosing ARIMA as the model type and then selecting:
If we apply the seasonal random trend model to the deflated auto sales data, using data up to November '91, we obtain the following picture:

Notice that the one-step-ahead predictions (up to November '91) respond very quickly to cyclical upturns and downturns in the data, unlike those of the seasonal random walk model. Also notice that the predictions for future seasonal cycles have exactly the same shape as the last observed seasonal cycle (the one ending in November '91). However, the long-term forecasts march off with a downward trend equal to the downward trend that was observed from November '90 to November '91. The confidence limits for the long-term forecasts also diverge very rapidly because of the assumption that the actual future trend will be randomly changing.
If we recompute the forecasts using data up to January '92, we see a very different picture in the long-term forecasts:

The upward trend between January '91 and January '92 now causes the long-term forecasts to shoot off upward! Thus, we see that the seasonal random trend model is much more responsive than the seasonal random walk model to sudden shifts in the data. This serves it well when forecasting one period ahead, but renders it rather unstable for purposes of forecasting many periods ahead.
If you are thinking at this point that it probably would be better to do some amount of smoothing when estimating the seasonal pattern and/or the long-term trend in the forecasts, you are right. (By "smoothing" I mean that you might want to average over the last few season's data when estimating the seasonal pattern and/or the trend.) You can smooth the trend estimate by adding MA=1 to the parameter specifications, and you can smooth the estimate of the seasonal pattern by setting SMA=1. Adding both of these terms will yield an "ARIMA(0,1,1)x(0,1,1) model," which is probably the most commonly used ARIMA model for seasonal data. (For the technically curious, setting MA=1 adds a multiple of the one-month-prior forecast error to the right-hand-side of the forecasting equation, while setting SMA=1 adds a multiple of the 12-month-prior error, and adding both terms together also causes a multiple of the 13-month-prior error to be included. The resulting model is a kind of "seasonal linear exponential smoothing.") The forecasts generated by this model from time origin November '91 indeed show a smoother seasonal pattern, a more conservative trend estimate, and narrower confidence intervals:

The preceding qualitative observations are confirmed by the model comparison report for the seasonal random walk, seasonal random trend, and more elaborate ARIMA models fitted to the deflated auto sales data. The seasonal random trend model outperforms the seasonal random walk model within the estimation and validation periods (i.e., for all one-step-ahead forecasts), and the more elaborate models with additional ARIMA parameters improve on the simpler models without those parameters. (Return to top of page.)