
If the seasonal difference (i.e., the season-to-season change) of a time series looks like stationary noise, this suggests that the mean (constant) forecasting model should be applied to the seasonal difference. For monthly data, whose seasonal period is 12, the seasonal difference at period t is Y(t)-Y(t-12). Applying the mean model to this series yields the equation:
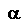
...where alpha is the the mean of the seasonal difference--i.e., the average annual trend in the data. Rearranging terms to put Y(t) on the left, we obtain:
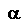
This forecasting model will be called the seasonal random walk model, because it assumes that each season's values form an independent random walk. Thus, the model assumes that September's 's value this year is a random step away from September's value last year, October's value this year is a random step away from October's value last year, etc., and the mean value of every step is equal to the same constant (denoted here as alpha). That is,
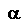
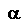
and so on. Notice that the forecast for Sep'96 ignores all data after Sep'95--i.e., it is based entirely on what happened exactly one year ago.
A seasonal random walk model is a special case of an ARIMA model in which there is one order of seasonal differencing, a constant term, and no other parameters--i.e., an "ARIMA(0,0,0)x(0,1,0) model with constant." To specify a seasonal random walk model in Statgraphics, choose ARIMA as the model type and use the following settings:
The seasonal difference of the deflated auto sales data (AUTOSALE/CPI) does not quite look like stationary noise: it is rather highly correlated. If we fit the seasonal random walk model anyway (using the ARIMA option in Statgraphics), we obtain the following forecast plot:
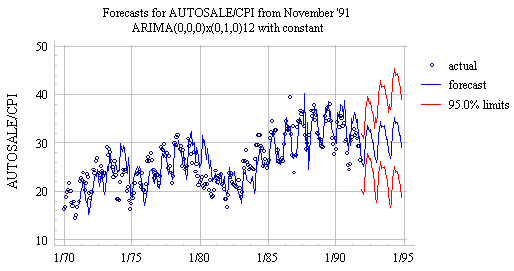
The distinctive feature of the forecasts produced by this model is that future seasonal cycles are predicted to have exactly the same shape as the most recently completed seasonal cycle, and the trend in the forecasts equals the average trend calculated over the whole history of the time series. If you look closely at the plot, you will notice that the model does not respond very quickly to cyclical upturns and downturns in the data: it is always looking exactly one year behind and assuming that the current trend equals the average trend, so that when the trend takes a cyclical upward or downward turn, the forecasts may miss badly in the same direction for many months in a row. Thus, the one-step-ahead forecast errors typically show positive autocorrelation. However, the long-term forecasts beyond the end of the sample appear reasonable insofar as they assume that the average trend in the past will eventually prevail again in the future.
Another distinctive feature of the seasonal random walk model is that it is relatively stable in the presence of sudden changes in the data--indeed, it doesn't even notice them for 12 months! For example, the previous plot shows long-term forecasts produced from time origin November 1991, at the end of a downward cycle. A few months later, the data begins to trend upward, but the long-term forecasts produced by the seasonal random walk model look much the same as before:
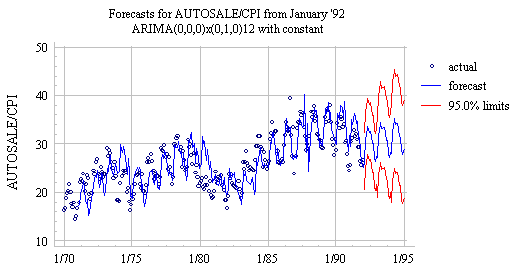
The positive autocorrelation in the errors of the seasonal random walk model can be reduced by adding a lag-1 autoregressive ("AR(1)") term to the forecasting equation. (In Statgraphics, you would do this by additionally setting AR=1). This yields an "ARIMA(1,0,0)x(0,1,0) model with constant," and its performance on the deflated auto sales series (from time origin November 1991) is shown here:
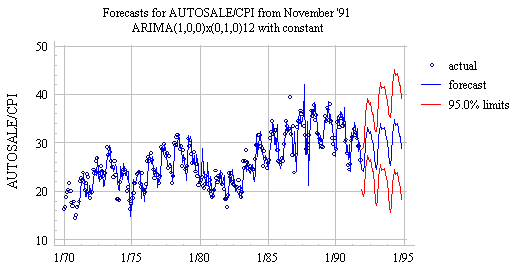
Notice the much quicker reponse to cyclical turning points. The in-sample RMSE for this model is only 2.05, versus 2.98 for the seasonal random walk model without the AR(1) term. (Return to top of page.)