Statistics
review and the simplest forecasting model: the sample mean (pdf)
Notes on the random
walk model (pdf)
Mean (constant) model
Linear trend model
Random walk model
Geometric random walk model
Three types of forecasts: estimation, validation, and the
future
Random walk model
When faced
with a time series that shows irregular growth, such as X2 analyzed earlier, the best strategy
may not be to try to directly predict the level of the series at each
period (i.e., the quantity Yt). Instead, it may
be better to try to predict the change that occurs from one period to
the next (i.e., the quantity Yt - Yt-1). That is, it may be better to look at the
first difference of the series, to see if a
predictable pattern can be found there. For purposes of one-period-ahead
forecasting, it is just as good to predict the next change as to predict the
next level of the series, since the predicted change can be added to the
current level to yield a predicted level. The simplest case of such a model is
one that always predicts that the next change will be zero, as if the series is
equally likely to go up or down in the next period regardless of what it has
done in the past.
Here's a
picture that illustrates a random process for which this model is appropriate:

In each
time period, going from left to right, the value of the variable takes an
independent random step up or down, a so-called random walk. If up and down movements are equally likely at each
intersection, then every possible left-to-right path through the grid is
equally likely a priori. See this
link for a nice simulation. A commonly-used analogy is that of a drunkard
who staggers randomly to the left or right as he tries to go forward: the path
he traces will be a random walk.
For
a real-world example, consider the daily US-dollar-to-Euro exchange rate. A
plot of its entire history from January 1, 1999, to December 5, 2014 (4006
observations) looks like this:
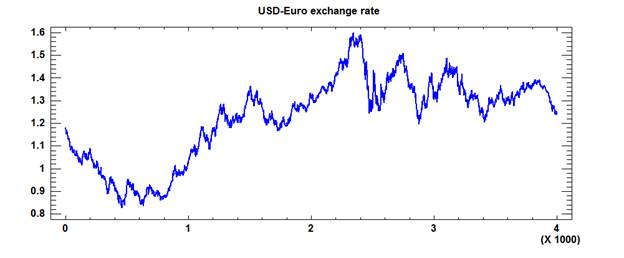
The historical
pattern looks quite interesting, with many peaks and valleys.
("Chartists" often try to extrapolate such patterns by fitting local
trend lines or curves, which I do not recommend. On average, 49% of them will correctly
guess the direction in which the market will move between today and some given
future date.) Now, here's a plot of the daily changes (first difference):
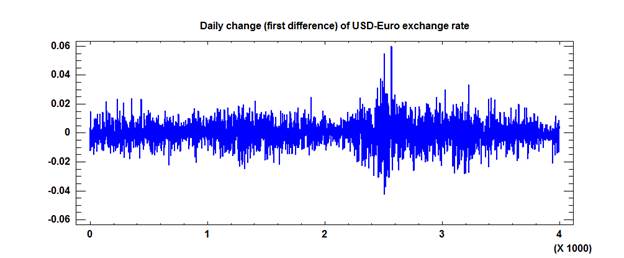
The
volatility (variance) has not been constant over time, but the day-to-day
changes are almost completely random, as shown by a plot of their autocorrelations:

The autocorrelation at lag k is the
correlation between the variable and itself lagged by k periods. If the values in
the series are completely random in the sense of being statistically
independent, the true values of the autocorrelations are zero, and the
estimated values should not be significantly different from zero. The red lines
on this plot are significance bands for testing whether the autocorrelations of
the daily changes are different from zero at the 0.05 level of significance,
and overall they are not. In particular, they are completely insignificant at
the first few lags and there is no systematic pattern. (For large samples,
autocorrelations are significantly different from zero at the 0.05 level if
their magnitude exceeds plus-or-minus two
divided by the square root of the sample size. Here the sample size is
4006, and 2/SQRT(4006) is approximately 0.03, as seen in the location of the
red lines on the plot.)
The
forecasting model suggested by these plots is one that merely predicts no change from the one period to the
next, because past data provides no information about the direction of future
movements:
Ŷt = Yt-1
This is
the so-called random-walk-without-drift
model: it assumes that, at each point in time, the series merely takes a
random step away from its last recorded position, with steps whose mean value
is zero. If the mean step size is some nonzero value α, the process is
said to be a random-walk-with-drift, whose prediction
equation is Ŷt = Yt-1 + α. The drunkard in
the picture above is missing one shoe, so he was probably drifting.
In general
the steps could be be discrete or continuous random variables, and the time
scale could also be discrete or continuous. Random walk patterns are commonly
seen in price histories of financial assets for which speculative markets
exist, such as stocks and currencies. This does not mean that movements in
those prices are random in the sense of being without purpose. When they go up
and down, it is always for a reason! But the direction of the next move cannot
be predicted ex ante: it can only be explained ex post, because if the
direction and magnitude of the next price movement could have been predicted in
advance, then speculators would already have bid it up or down by that amount.
Random walk patterns are also widely found elsewhere in nature, for example, in
the phenomenon of Brownian
motion that was first explained by Einstein. (Return to top
of page.)
It is
difficult to tell whether the mean step size in a random walk is really zero,
let alone estimate its precise value, merely by looking at the historical data
sample. If you simulate a random walk process (for example, by building a
spreadsheet model that uses the RAND() function in the formula for generating
the step values), you will typically find that different iterations of the same
model will yield dramatically different pictures, many of which will have
significant-looking trends, as shown in the simulation
link mentioned above. In fact, the same model will usually yield both
upward and downward trends in repeated iterations, as well as
interesting-looking curves that seem to demand some sort of complex model. This
is just a statistical illusion, like the so-called "hot hand in
basketball" and other examples of "streakiness" in sports. Your
brain tries hard to find patterns, even when they are not there. See the Hot Hand in Sports web site for more
on this.
In
applications, it is best to draw on other sources of information and on
theoretical considerations in deciding whether to include a drift term in the
model, and if so, how to estimate its value. In the case of exchange rates,
there is no reason to assume a long-term trend in one direction or the other,
at least, not a trend that would stand out against the noise. The mean daily
change is 0.000012 for this sample of exchange rate data, and the standard
error of the mean is 0.00012, so the sample mean is different from zero by only
1/10th of a standard error, which is not significant by any measure.
Again, though, the mean value of the steps in a finite sample of random-walk
data generally does not provide a good estimate of the current rate of drift,
if any.
Overall,
then, it appears that a random-walk-without-drift model is appropriate for this
time series. If the model is fitted to the entire history of the daily data,
going back to 1999, the forecasts and 50% confidence limits produced by the
model look like this:

(This
chart was produced by Statgraphics. 50% rather than 95% limits are shown merely
to make them fit better in the picture. There is nothing special about 95%
anyway, apart from convention.) Here is a close-up view of the actual data
points and forecasts at the very end of the series:

The key
properties of the model that are illustrated by this graph are the following:
a. The one-step-ahead forecasts within the sample
follow exactly the same path as the data, except that they lag behind by one period. (You must look
carefully to see this: at first glance it may appear that the model fits the
data perfectly, but in fact it is making errors in every period, and those
errors are independent random variables.)
b. The long-term forecasts outside the sample
follow a horizontal straight line anchored on the last observed value,
because no upward or downward drift or any other systematic time pattern is
assumed. (If non-zero drift was assumed, this line might slope upward or downward.)
c. The confidence bands for long-term forecasts grow
wider in a fashion that looks like a sideways
parabola, for reasons explained below. (Return to top of
page.)
In the
random-walk-without-drift model, the standard error of the 1-step ahead forecast
is the root-mean-squared-value of the period-to-period changes in the data
sample, i.e., it is the square root of the average of squared values of the
first difference of the series. For a random-walk-with-drift, the forecast standard error is the sample standard deviation of the period-to-period changes. (The
difference between the RMS value and the standard deviation of the changes is
usually negligible unless the volatility is very small in comparison to the
drift.)
The error
that the model makes in a k-step-ahead
forecast is the sum of k independently and identically distributed random
variables, because the model continues to make the same prediction while the
variable takes k random steps. Because the variance of a sum of independent
random variables is the sum of the variances, it follows that the variance of
the k-step-ahead forecast error is larger than that of the one-period-ahead
forecast by a factor of k. And because the standard deviation of the forecast
error is the square root of its variance, it follows that the standard error of a k-step-ahead forecast
is larger than that of the 1-step-ahead forecast by a factor of
square-root-of-k. This is the so-called "square root of time"
rule for the errors of random walk forecasts, and it explains the
sideways-parabola shape of the confidence bands for long-term forecasts: that's
the shape of the graph of Y=SQRT(X).
For this
very large data sample, the root-mean-squared value and the sample standard
deviation of the daily changes are both equal to 0.00778 to 3 significant
digits, so the standard error of a k-step ahead forecast error is
0.00778*SQRT(k), and confidence limits are calculated from it in the usual way.
A 95% interval is (approximately) the point forecast plus-or-minus 2 standard
errors, and a 50% confidence interval is the point forecast plus-or-minus
two-thirds of a standard error.
In the
case of the exchange rate data, it is not really appropriate to use the entire
sample to estimate the standard deviation of the daily changes, because it
clearly has not been constant over time. A shorter data history could be used
to address this problem, and other kinds of information such as prices of
foreign-exchange options could also be considered.
The random
walk model may look trivial if you have never seen it before: what could be
more simple-minded than always predicting that tomorrow will be the same as
today? This does not even require any knowledge of statistics! For that reason
it is sometimes called the "naive model." It is not at all trivial,
however. The square-root-of-time pattern in its confidence bands for long-term
forecasts is of profound importance in finance (it is the basis of the theory
of options pricing), and the random walk model often provides a good benchmark
against which to judge the performance of more complicated models.
The random
walk model can also be viewed as an important special case of an ARIMA model ("autoregressive
integrated moving average"). Specifically, it is an
"ARIMA(0,1,0)" model. More general ARIMA models are capable of
dealing with more interesting time patterns that involve correlated steps, such
as mean reversion, oscillation, time-varying means, and seasonality. These
topics are discussed in detail in the ARIMA pages of these notes.
For a much more
complete discussion of the random walk model, illustrated by a shorter sample
of the exchange rate data, see the "Notes on the random
walk model" handout.
