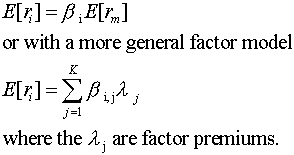
Copyright 1995 by Campbell R. Harvey. All rights reserved. No part of this lecture may be reproduced without the permission of the author.
According to Fama:
"An efficient capital market is a market that is efficient in processing information. The prices of securities at any time are based on correct evaluation of all information available at that time. In an efficient capital market, prices fully reflect available information."
We will be concerned with how well the market absorbs new information. In order to tell if the market adjusts to information, you need a pricing model. For example, in the last lecture, we considered the performance a mutual fund: Franklin Income. We assumed that the beta of Franklin was 1.00. We then showed that Franklin's performance was below the market's risk adjusted expectation. Suppose that we estimated the beta to be 0.5. Then Franklin made a very large abnormal return. Is this evidence of market efficiency? Franklin is just a portfolio of NYSE stocks. How could the fund managers consistently pick the right stocks over 15 years?. We cannot conclusively state that the market is inefficient because the model that we use to risk adjust could be incorrect. People may view Franklin as a lot more risky than the beta indicates. As a result, we must always condition our statements about market efficiency in terms of the model that we are using to test efficiency.
Hence, any test of efficiency, is a joint test of efficiency and the pricing model. This means that given a certain pricing model, you might find evidence against market efficiency. But another hypothesis is that the market if efficient and you are using the wrong pricing model. This is a common dilemma in testing joint hypotheses.
As previously defined, in an efficient market, prices are set to fully reflect all relevant information. There are three types of efficiency which are based on different notions of what type of information is understood to be relevant.
No investor can earn abnormal returns by developing trading rules based on historical price or return information. Information from past returns is available at a very low cost. It makes sense that these past returns cannot be used to forecast future returns. Most people would agree that weak-form efficiency holds.
No investor can earn abnormal returns from trading rules based on any publicly available information. Examples of publicly available information are: annual reports of companies, investment advisory data such as "Heard on the Street" in the Wall Street Journal, or ticker tape information. All of this information is relatively inexpensive to collect.
No investor can earn abnormal returns using any information -- private or public. Private information is usually very costly to collect. Almost nobody believes that markets are strongly efficient.
If a market exhibits weak-form efficiency, then it is impossible to earn abnormal returns by developing a forecasting model based on past returns. The first thing we have to deal with is the definition of abnormal returns. In the context of the Capital Asset Pricing Model, an abnormal return is defined as the return in excess of what was expected according to the CAPM equation. The CAPM suggests that the only variables that we need in calculating the expected return on security i are: the riskfree rate (a constant), the expected excess return on the market, and the security's beta (a constant). A similar implication holds for the APT. The expected excess return is a function of the factor loading times the factor premium.
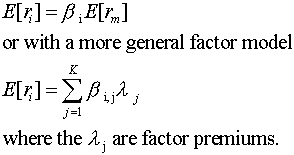
There are no additional variables that should be included in this equation.
We will carry out a test of weak-form market efficiency by trying to forecast IBM's stock return with a past IBM stock return. The model we will consider is:

The weak-form hypothesis tells us that the delta_1 coefficient should be indistinguishable from zero.
Consider the results of the following regressions. I have provided some results for IBM from 1926--1984. The returns data comes from the Center for Research in Security Prices (CRSP).
Time delta_0 t-stat delta_1 t-stat R^2
1926-94 .0142 5.7 0.08 2.2 .01
1926-35 .0197 2.1 0.09 0.9 .00
1936-45 .0105 2.3 -0.10 -0.2 .00
1946-55 .0180 3.4 0.02 0.2 .00
1956-65 .0184 3.0 0.14 1.5 .01
1966-75 .0087 1.2 0.09 0.9 .00
1976-85 .0123 2.4 0.09 1.0 .00
1986-94 .0060 1.4 0.05 0.6 .00
1971-75 .0017 0.2 0.88 0.1 .00
1976-80 .0077 1.1 0.87 0.3 .00
1981-85 .0166 2.2 0.77 0.9 .00
1986-90 .0070 0.8 0.89 0.7 .00
1990-94 .0050 0.8 0.97 0.4 .00
The results indicate that the delta_1 coefficient is two standard errors from zero only in the overall period. In all the sub-periods, the coefficient is indistinguishable from zero. The best R^2 from all of the regressions is 1%. It is hard to see a successful trading rule being built from a model that explains only 1% of the variation in returns. The regressions with the IBM stock returns do not provide any evidence against the weak-form version of the efficient market hypothesis.
We have already informally evaluated the performance of the Franklin Income fund. Now that we have the asset pricing model we can say something about risk adjusted performance. In this section, we will develop three measures to evaluate the performance of a mutual fund or a portfolio.
There are two major types of investment funds: closed-end and open-end. After the initial offering of shares, the management of the closed-end fund cannot offer additional shares to the public. Investors can redeem their shares to reduce the number of shares outstanding. The management of the open-end fund can offer new shares at any time. The open-end funds are known as mutual funds.
Open a copy of the Wall Street Journal. Notice that most companies have multiple listings. The Franklin Group has about 20 funds ranging from Gold to Utilities. The first number beside the fund category is NAV or net asset value. The second number is the offer price for a share of the fund. The third is the change in net asset value over the trading day.
I have also attached some bar charts that compare this risk of various mutual fund types to their excess return. Note that the income fund is the most conservative. The market risk beta and total risk (standard deviation of return) are the lowest. The maximum capital gain fund has the highest market risk and a high total risk. The chart below suggests that the higher risk is rewarded with higher return.



The first measure of performance is called the Jensen index. It is simply the alpha. Portfolio i average excess return is:

The CAPM predicted excess return is:

So the alpha is:
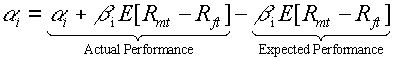
Thus, the alpha measure risk adjusted performance of a security. The alpha is the Jensen index.
In his 1969 paper, Michael Jensen runs time series regressions for 115 open-end mutual funds from 1945 to 1964. He found that the average alpha was negative, -.011. I have provided a graph of the distribution of alpha from another study. The distribution is centered around zero. This suggests that mutual funds on average do not do better than the market on a risk adjusted basis. I have also provided a graph of the t-statistics for the alphas. Only 5% of the funds had a t-statistic that is greater than two. This provides support for the semi-strong version of the efficient market hypothesis. The mutual funds have not shown any abnormal performance. If we take into consideration transactions costs, the mutual funds have done worse than a passive market portfolio.

I have also included some charts which update Jensen's study based on work by Campbell Harvey and Ravi Bansal "Performance Evaluation in the Presence of Dynamic Trading Strategies." I provide both a histogram of the alphas as well as the t-statistics. The alpha* is a new measure of performance evaluation which is detailed in our paper. Instead of assuming that some market index like the S&P 500 is efficient, we choose an index which is exactly efficient.


I have included a diagram of three scenarios of superior market performance. In all of the panels, the excess returns on the fund are plotted against the excess returns on the market. Notice that the regression line in the first panel has a positive intercept. This is the measure of abnormal performance.

The second panel shows what is known as market timing. If the portfolio manager knows when the stock market is going to go up, he will shift into high beta stocks. These stocks will go up even further than the market. If the portfolio manager knows the market is going to go down, he will switch into low beta stocks which will go down less than the market. This accounts for the bowed shape of the data. Notice that the Jensen measure is positive signalling superior performance.
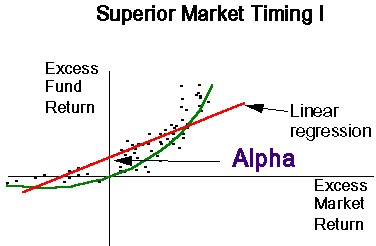
The third panel shows another market timing example. In this case, the manager is so good that there are no negative returns. The manager exhibits good market timing abilities. When the market goes up, the fund goes up by more than the market -- indicating a shift into high beta stocks. It is important to notice that the Jensen measure or intercept is negative. So even though this manager has exhibited strong market timing abilities, the performance evaluation criteria suggests he is not doing a superior job. This is a major problem with the Jensen measure.

We have already been introduced to the Sharpe measure of investment performance. The term
E_i-R_f
S_i = -------
STD_i
is known as the Sharpe measure or the Sharpe index.
This index uses the Capital Market Line as the benchmark.
Below is a graph depicting the expected return--standard deviation
space. The Sharpe measure is the slope of the line from R_f
(rise is E_i-R_f over
run which is STD_i. The intercept is the riskfree rate, R_f.
The higher the Sharpe measure is the better the security
looks.
Note that if the mutual fund is positioned on the Capital Market Line, then the fund has neutral performance. This makes sense under the CAPM, because, on the basis of public information alone, any investor can construct a portfolio that is positioned on the CML. The higher the Sharpe measure the larger the excess return per unit of standard deviation. Higher Sharpe measures are associated with superior performance.
The Treynor index uses the Security Market Line as a benchmark. Remember that the Security Market Line is drawn in return--beta space. The measure is defined as:
E_i-R_f
T_i = -------
beta_i
The index measures the excess return per unit of risk taken. The
index has a geometric interpretation that is similar
to the Sharpe index. The Treynor index measures the slope
of a line that starts at the riskfree rate and connects with
the point that marks the fund's beta and expected return.
The higher the Treynor index the more return the fund is making per unit of risk it is taking. The benchmark line is the security market line which has a slope of E[R_m]-R_f. If the fund has a Treynor index equal to E[R_m]-R_f, then the fund exhibits neutral performance. A higher Treynor index indicates superior performance.
A plot of the SML and individual mutual funds is provided.

Note that the SML is drawn with excess returns on the y-axis. This does not change the magnitude of the Treynor index. The SML is the dashed line that starts at zero in the excess return axis. Notice that the mutual funds are distributed randomly above and below the SML. This suggests that mutual funds did not systematically outperform the market.
Graham and Harvey propose two additional measures of performance that are related to the Sharpe measure. Given a mutual fund's volatility, we create a portfolio of the S&P 500 futures and a money market account that exactly replicates the fund volatility. Graham-Harvey measure 1 is the difference between the mutual fund return and the "passive" futures return.
The second measure is the following. Given the volatility of the S&P 500 futures, we lever the mutual fund volatility up or down (by borrowing and lending respectively) to exactly match the S&P 500 volatility. The difference between the fund return and the S&P 500 return is the Graham-Harvey measure 2.
A description of the Graham-Harvey method is detailed in a recent Forbes article.
Forbes, June 19, 1995 page 160.
Forbes, June 19, 1995 page 161.
I have presented a number of different ways to evaluate the performance of mutual funds. There is a considerable literature that suggests that after expenses the mutual funds have not outperformed the market on a risk adjusted basis. Perhaps the most interesting issue has to do with the persistence of returns. The following chart is from Jensen (1969).
Number of Consecutive Years Fund Proportion of Group with Performance Performance Exceeded That of a Exceeding That of a Passive Portfolio Passive Portfolio with Equal with Equal Market Risk in the Market Risk Subsequent Year (%)
1 50.4
2 52.0
3 53.4
4 55.8
5 46.4
Notice that it is fairly random whether the funds do better than a passive portfolio constructed to have the same market risk as the fund. The evidence suggests that fund managers are extracting management fees and delivering performance that could be equaled on average by holding a combination of Treasury bills and the market portfolio.
While the mutual fund performance supports the idea of markets being semi-strong efficient, the recommendations of the Value Line Investment Survey provide a counterexample. Value Line ranks stocks on the basis of timeliness. The scale runs from 1 to 5. A rank of 1 means that Value Line expects the stock to appreciate in value. A rank of 5 means that Value Line believes that it is unlikely that there will be any appreciation in the stock value. All of the information that Value Line uses in determining the forecast comes from publicly available information. A graph of Value Line's performance is attached.
One of the first studies of the quality of the Value Line recommendations was done by Black (1970). He found that by purchasing a portfolio of the rank 1 stocks and short-selling a portfolio of rank 5 stocks that you could earn 20% per year on a risk adjusted basis. This ran counter to the efficient markets hypothesis.
Copeland and Mayers (1982) investigate whether abnormal returns could be made by following Value Line's recommendations. They find that buying portfolio 1 and selling portfolio 5 earns 6.8% per year. The betas for the portfolio 1 and portfolio 5 are very close to one. Hence, we can consider the 6.8% a risk adjusted return. The return is much lower than 20% that Black (1970) found. In fact, Copeland and Mayers find that the size of the abnormal return has been consistently dropping through time.
Some of the strongest evidence that Copeland and Mayers gather is from the change portfolios. They form portfolios that buy stocks that Value Line has moved up in the rankings and sell stocks that Value Line has moved down in the rankings. There are significant abnormal returns if this strategy is following. Furthermore, these returns tend to persist over time. Finally, the existence of transactions costs cannot explain the size of these abnormal returns.
The Value Line performance appears to run counter to the semi-strong version of the efficient market's hypothesis. But we cannot say for sure that the market is not efficient. This is because we are jointly testing the model (CAPM) and market efficiency. If the model is incorrect, then we may be incorrectly rejecting market efficiency.
However, it is not clear that anything is going on with the Value line ratings. The mutual funds which follow Value Line strategies have shown no evidence of out performing naive benchmarks.
Graham and Harvey study the performance of over 200 investment newsletters which recommend mixes of equities and cash. The following details the performance of all newsletter portfolios.

We also examined newsletters which existed for four years or more in the sample (some only existed for a few months).

One question that we examine is whether equity weights increase before positive market returns. This is the definition of market timing. There is no evidence of timing the positive returns

We also examined whether equity weights decrease before negative market returns. This is also market timing. There is no evidence of timing the negative returns

Suppose we estimate the alphas for a number of funds over a three year period. Can we use those alphas to predict next period's alphas? Does superior performance in the past indicate a high probability of superior performance in the future? Does poor performance in the past indicate future poor performance?
Consider the following cross-sectional predictive regression:

A positive theta_1 will indicate that performance persists.
The evidence suggests that evidence of persistence. However, most of the persistence is coming from poor performance. That is, poor performers are likely to be poor performers in the future.
The following is a contingency table which examines whether performance persists in 8 different style categories of Morningstar.
 Aggressive Growth
Funds
Aggressive Growth
Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 26 | 10 | 36 |
| alpha < 0 | 4 | 1 | 5 | |
| Total | 30 | 11 | 41 | |
 Growth-Income
Funds
Growth-Income
Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 30 | 53 | 83 |
| alpha < 0 | 42 | 41 | 83 | |
| Total | 72 | 94 | 166 | |
 Specialty Funds
Specialty Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 38 | 8 | 46 |
| alpha < 0 | 36 | 30 | 66 | |
| Total | 74 | 38 | 112 | |
 Equity Income
Funds
Equity Income
Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 2 | 2 | 4 |
| alpha < 0 | 14 | 23 | 37 | |
| Total | 16 | 25 | 41 | |
 Hybrid
(equity) Funds
Hybrid
(equity) Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 2 | 2 | 4 |
| alpha < 0 | 68 | 59 | 127 | |
| Total | 70 | 61 | 131 | |
 Small Company
Funds
Small Company
Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 60 | 9 | 69 |
| alpha < 0 | 15 | 3 | 18 | |
| Total | 75 | 12 | 87 | |
 Growth Funds
Growth Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 90 | 99 | 189 |
| alpha < 0 | 46 | 32 | 78 | |
| Total | 136 | 131 | 267 | |
 International
Funds
International
Funds
| 1992-1995 | ||||
| alpha > 0 | alpha < 0 | Total | ||
| 1989-1992 | alpha > 0 | 4 | 2 | 6 |
| alpha < 0 | 50 | 40 | 90 | |
| Total | 54 | 42 | 96 | |
Additional analysis is available for:
There are many new studies that show that stock returns at time t can be forecasted with information based at time t-1. For example, Harvey (1989) (P3) shows that up to 18% of the variation in U.S. stock portfolios can be forecasted on a monthly basis. Harvey (1991) (P10) finds similar results with international data.
Many people argue that predictability implies inefficiency. However, this is not necessarily true. Consider the conditional CAPM examined by Harvey (1989). The CAPM restricts the conditionally expected returns to be linearly related to conditionally expected excess returns on a market wide portfolio. The coefficient in the linear relation is the asset's beta or the ratio of the conditional covariance with the market to the conditional variance of the market.
Predictability could be driven by changing risk (changing conditional covariance), changing market volatility or changes in the expected returns of the market as a whole. If these changes in risk and volatility are predictable, then it follows that the stock returns for asset j are also predictable.
Ferson and Harvey (1991a) (P5) and (1991b) (P7) find that most of the predictability in stock and bond returns can be attributed to predictable shifts in risks and the market wide reward for risks (risk premiums). They consider a multi-risk formulation and find that the risk and risk premium associated with the market return (like in the single risk CAPM) is by far the most important component in explaining the predictabilility of returns. In another decomposition, they find that changing risk premiums -- rather than changing betas -- account for the bulk of the predictability. Their evidence suggests that predictable returns result from predictable shifts in risk and risk premiums rather than some market inefficiency.
The new conditional approach to asset pricing and asset allocation has an important implication for performance evaluation. Suppose there is a portfolio manager that is using the today's available information to determine expected returns, conditional variances and covariances. Based upon these conditional measures, she constructs an efficient portfolio. Every month the programs are rerun and she adjusts her portfolio to be on the conditional mean-variance frontier. This is clearly as good as one can do in portfolio management.
Now suppose that we evaluate her performance. It is not fair to evaluate this person based upon realized risk -- such as the method of Sharpe, Treynor, Jensen or Graham-Harvey. The portfolio strategy was based upon the forecast of risk. Realized risk or average risk over the evaluation period is unlikely to be the same as the conditional risk.
This is the key insight. One may reject the mean-variance efficiency of a portfolio based upon average measure. This rejection does not imply that the portfolio is conditionally mean-variance inefficient. In other words, we may incorrectly fire the portfolio manager if we are using the average risk and average return measures.
Conditional portfolio evaluation is possible. Harvey (1989) first proposes the conditional analogue to Jensen's (1969) measure:

where alpha_i represents the performance in excess of the conditionally expected performance based upon the conditional risk of the portfolio.
The idea pursued in Bansal and Harvey (1995) is that it is naive to evalate managers relative to passive indices. That is, the managers should be using information to dynamically rebalance their portfolios to capture any predictability in asset returns.
When we allow for dynamic strategies, the performance of the managers becomes even more disappointing. The following is the distribution of the conditional alphas. Notice that our sample has an extreme survivorship bias. We sample the mutual funds which have existed from 1968-1993. This should positively bias performance! However, there is no evidence of this.

The t-ratios for the alphas are presented below.

We also ask the question of whether managers do better (in risk adjusted terms) in recessions or expansions. We find that managers tend to underperform the most during expansions. The CAPM alphas

Using our r* benchmark, a similar conclusion is reached.

Finally, we draw the mean-variance frontier which includes the passive strategies as well as dynamic strategies which are functions of known information (e.g. increase equity weight for time t if the interest rate drops during month t-1).
We draw a four standard error range around the frontier and not one fund penetrates the lower bound. Notice that this frontier is drawn with three assets: the T-bill, T-bond and S&P 500. The idea is that these benchmark assets can be easily traded in the futures market. Along with the three benchmarks, we include dynamic strategies which are simply the benchmark at time t multiplied by information (such as the interest rate) at time t-1
