Notes on linear
regression analysis (pdf file)
Introduction
to linear regression analysis
Mathematics of
simple regression
Regression examples
·
Beer sales vs. price, part 1: descriptive
analysis
·
Beer sales vs. price, part 2: fitting a simple
model
·
Beer sales vs. price, part 3: transformations
of variables
·
Beer sales vs.
price, part 4: additional predictors
·
NC natural gas
consumption vs. temperature
·
More regression datasets
at regressit.com
What to look for in
regression output
What’s
a good value for R-squared?
What's the bottom line? How to compare models
Testing the assumptions of linear regression
Additional notes on regression
analysis
Stepwise and all-possible-regressions
Excel file with
simple regression formulas
Excel file with regression formulas
in matrix form
Notes on logistic regression (new!)
If you use
Excel in your work or in your teaching to any extent, you should check out the
latest release of RegressIt, a free Excel add-in for linear and logistic
regression. See it at regressit.com. The linear regression version runs on both PC's and Macs and
has a richer and easier-to-use interface and much better designed output than
other add-ins for statistical analysis. It may make a good complement if not a
substitute for whatever regression software you are currently using,
Excel-based or otherwise. RegressIt is an excellent tool for
interactive presentations, online teaching of regression, and development of
videos of examples of regression modeling. It includes extensive built-in
documentation and pop-up teaching notes as well as some novel features to
support systematic grading and auditing of student work on a large scale. There
is a separate logistic
regression version with
highly interactive tables and charts that runs on PC's. RegressIt also now
includes a two-way
interface with R that allows
you to run linear and logistic regression models in R without writing any code
whatsoever.
If you have
been using Excel's own Data Analysis add-in for regression (Analysis Toolpak),
this is the time to stop. It has not
changed since it was first introduced in 1993, and it was a poor design even
then. It's a toy (a clumsy one at that), not a tool for serious work. Visit
this page for a discussion: What's wrong with Excel's Analysis Toolpak for regression
Mathematics
of simple regression
Formulas
for the slope and intercept of a simple regression model
Formulas for
R-squared and standard error of the regression
Formulas
for standard errors and confidence limits for means and forecasts
To set the stage for discussing the formulas
used to fit a simple (one-variable) regression model, let′s briefly
review the formulas for the mean
model, which can be considered as a constant-only (zero-variable)
regression model. You can use
regression software to fit this model and produce all of the standard table and
chart output by merely not selecting any independent variables. R-squared will be zero in this case,
because the mean model does not explain any of the variance in the dependent
variable: it merely measures it.
The forecasting equation of the mean model
is:
![]()
...where b0 is the sample mean:
![]()
The sample mean has the (non-obvious)
property that it is the value around
which the mean squared deviation of the data is minimized, and the same
least-squares criterion will be used later to estimate the "mean
effect" of an independent variable.
The error that the mean model makes for
observation t
is therefore the deviation of Y from
its historical average value:
![]()
The standard
error of the model, denoted by s, is
our estimate of the standard deviation
of the noise in Y (the variation in it that is considered unexplainable).
Smaller is better, other things being equal: we want the model to explain as
much of the variation as possible. In the mean model, the standard error of the
model is just is the sample standard deviation of Y:
![]()
(Here and elsewhere, STDEV.S denotes the sample standard deviation of X, using Excel
notation. The population standard
deviation is STDEV.P.) Note that the
standard error of the model is not
the square root of the average value of the squared errors within the
historical sample of data. Rather, the sum of squared errors is divided by n-1 rather than n under the square root
sign because this adjusts for the fact that a "degree of freedom for error″
has been used up by estimating one model parameter (namely the mean) from the
sample of n data points.
The accuracy of the estimated mean is
measured by the standard error of the
mean, whose formula in the mean model is:
![]()
This is the estimated standard deviation of
the error in estimating the mean. Notice that it is inversely proportional to the
square root of the sample size, so it tends to go down as the sample size goes
up. For example, if the sample size is increased by a factor of 4, the standard
error of the mean goes down by a factor of 2, i.e., our estimate of the mean
becomes twice as precise.
The accuracy of a forecast is measured by the standard error of the forecast, which
(for both the mean model and a regression model) is the square root of the sum
of squares of the standard error of the model and the standard error of the
mean:
![]()
This is the estimated
standard deviation of the error in the forecast, which is not quite the same
thing as the standard deviation of the unpredictable variations in the data
(which is s). It takes into
account both the unpredictable variations in Y and the error
in estimating the mean. In the mean model, the standard error of the mean is a
constant, while in a regression model it depends on the value of the independent
variable at which the forecast is computed, as explained in more detail below.
The standard error of the forecast gets
smaller as the sample size is increased, but only up to a point. More data
yields a systematic reduction in the standard error of the mean, but it does not yield a systematic reduction in the
standard error of the model. The standard error of the model will change to
some extent if a larger sample is taken, due to sampling variation, but it
could equally well go up or down. The variations in the data that were
previously considered to be inherently unexplainable remain inherently
unexplainable if we continue to believe in the model′s assumptions, so
the standard error of the model is always a lower bound on the standard error
of the forecast.
Confidence
intervals
for the mean and for the forecast are equal to the point estimate plus-or-minus the appropriate standard error
multiplied by the appropriate 2-tailed critical value of the t distribution. The critical value
that should be used depends on the number of degrees of freedom for error (the
number data points minus number of parameters estimated, which is n-1 for this model) and
the desired level of confidence. It can be computed in Excel using the T.INV.2T function. So, for example, a
95% confidence interval for the forecast is given by
![]()
In
general, T.INV.2T(0.05, n-1)
is fairly close to 2 except for very small samples, i.e., a 95% confidence
interval for the forecast is roughly equal to the forecast plus-or-minus two
standard errors. (In older versions of Excel, this function was just called
TINV.) Return
to top of page.
Formulas for the slope and intercept of a simple
regression model:
Now let's regress. A simple regression model
includes a single independent variable, denoted here by X, and its forecasting
equation in real units is
![]()
It differs from the
mean model merely by the addition of a multiple of Xt to the forecast. The
estimated constant b0 is
the Y-intercept of the regression
line (usually just called "the intercept" or "the
constant"), which is the value that would be predicted for Y at X = 0. The estimated
coefficient b1 is the slope of the regression line, i.e., the
predicted change in Y per
unit of change in X.
The
simple regression model reduces to the mean model in the special case where the
estimated slope is exactly zero. The estimated slope is almost never exactly
zero (due to sampling variation), but if it is not significantly different from
zero (as measured by its t-statistic), this suggests that the mean model should
be preferred on grounds of simplicity unless there are good a priori reasons
for believing that a relationship exists, even if it is largely obscured by
noise.
Usually we do not
care too much about the exact value of the intercept or whether it is
significantly different from zero, unless we are really interested in what happens
when X goes to
"absolute zero" on whatever scale it is measured. Often X is a variable which
logically can never go to zero, or even close to it, given the way it is
defined. So, attention usually focuses mainly on the slope coefficient in the
model, which measures the change in Y to be expected per unit of change in X as both variables
move up or down relative to their historical mean values on their own natural
scales of measurement.
The coefficients, standard errors, and
forecasts for this model are obtained as follows. First we need to compute the coefficient of correlation between Y and X, commonly denoted by
rXY, which measures the
strength of their linear relation on a relative scale of -1 to +1. There are various formulas for it, but
the one that is most intuitive is expressed in terms of the standardized values of the
variables. A variable is
standardized by converting it to units of standard
deviations from the mean. The
standardized version of X
will be denoted here by X*,
and its value in period t
is defined in Excel notation as:
![]()
... where STDEV.P(X) is the population
standard deviation, as noted above.
(Sometimes the sample standard
deviation is used to standardize a variable, but the population standard
deviation is needed in this particular formula.) Y*
will denote the similarly standardized value of Y.
The
correlation coefficient is equal to the average product of the standardized
values of the two variables:
![]()
It is intuitively obvious that this statistic
will be positive [negative] if X and Y tend to move in the same
[opposite] direction relative to their respective means, because in this case X* and Y* will tend to have the same [opposite]
sign. Also, if X and Y are perfectly
positively correlated, i.e., if Y is an exact positive linear function of X, then Y*t = X*t for all t, and the formula for
rXY reduces to (STDEV.P(X)/STDEV.P(X))2, which is equal to 1. Similarly, an exact negative linear relationship yields
rXY = -1.
The
least-squares estimate of the slope coefficient (b1) is equal to the correlation
times the ratio of the standard deviation of Y to the standard deviation of X:
![]()
The ratio of standard deviations on the RHS
of this equation merely serves to scale the correlation coefficient
appropriately for the real units in which the variables are measured. (The
sample standard deviation could also be used here, because they only differ by
a scale factor.)
The least-squares
estimate of the intercept is the mean of Y minus the slope coefficient times the mean of X:
![]()
This equation implies that Y must be predicted to
be equal to its own average value whenever X is equal to its own average value.
The standard error of the model (denoted again by s) is usually referred
to as the standard error of the
regression (or sometimes the "standard error of the estimate") in
this context, and it is equal to the square
root of {the sum of squared errors divided by n-2}, or equivalently,
the standard deviation of the errors
multiplied by the square root of (n-1)/(n-2), where the latter
factor is a number slightly larger than 1:
![]()
The sum of squared
errors is divided by n-2 in this calculation rather than n-1 because an additional degree of freedom for
error has been used up by estimating two parameters (a slope and an intercept)
rather than only one (the mean) in fitting the model to the data. The standard error of the regression
is an unbiased estimate of the standard deviation of the noise in the data,
i.e., the variations in Y that
are not explained by the model.
Each of the two model parameters, the slope and
intercept, has its own standard
error, which is the estimated standard deviation of the error in estimating it.
(In general, the term "standard error" means "standard deviation
of the error" in whatever is being estimated. ) The standard error of the
intercept is
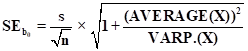
which looks exactly
like the formula for the standard error of the mean in the mean model, except
for the additional term of
(AVERAGE(X))2/VAR.P(X)
under
the square root sign. This term reflects the additional uncertainty about the
value of the intercept that exists in situations where the center of mass of the
independent variable is far from zero (in relative terms), in which case the
intercept is determined by extrapolation far outside the data range. The
standard error of the slope coefficient is given by:
![]()
...which also looks
very similar, except for the factor of STDEV.P(X) in the denominator. Note that s is measured in units
of Y and STDEV.P(X) is measured in units
of X, so SEb1 is measured (necessarily) in "units of Y per unit of X",
the same as b1 itself. The terms in
these equations that involve the variance or standard deviation of X merely serve to
scale the units of the coefficients and standard errors in an appropriate way.
You don′t need
to memorize all these equations, but there is one important thing to note: the standard errors of the coefficients are
directly proportional to the standard error of the regression and inversely
proportional to the square root of the sample size. This means that noise in
the data (whose intensity if measured by s) affects the errors in all the coefficient estimates in
exactly the same way, and it also means that 4 times as much data will tend to
reduce the standard errors of the all coefficients by approximately a factor of
2, assuming the data is really all generated from the same model, and a really
huge of amount of data will reduce them to zero.
However,
more data will not systematically reduce
the standard error of the regression. As with the mean model, variations that
were considered inherently unexplainable before are still not going to be
explainable with more of the same kind of data under the same model
assumptions. As the sample size gets larger, the standard error of the
regression merely becomes a more accurate estimate of the standard deviation of
the noise. Return to top of page.
Formulas for
R-squared and standard error of the regression
The fraction of the variance of Y that is
"explained" by the simple regression model, i.e., the percentage by
which the sample variance of the errors ("residuals") is less than
the sample variance of Y
itself, is equal to the square of the
correlation between them, i.e., "R squared":
![]()
Equivalently:
![]()
Thus, for example, if the correlation is rXY = 0.5, then rXY2 = 0.25, so the simple
regression model explains 25% of the variance in Y in the sense that the sample variance of the
errors of the simple regression model is 25% less than the sample variance of Y. This is not supposed
to be obvious. It is a "strange but true" fact that can be proved
with a little bit of calculus.
By taking square roots everywhere, the same
equation can be rewritten in terms of standard deviations to show that the standard deviation of the errors is
equal to the standard deviation of the dependent variable times the square root
of 1-minus-the-correlation-squared:
![]()
However, the sample
variance and standard deviation of the errors are not unbiased estimates of the variance and standard deviation of the unexplained
variations in the data, because they do not into account the fact that 2
degrees of freedom for error have been used up in the process of estimating the
slope and intercept. The fraction by which the square of the standard error of the regression is
less than the sample variance of Y (which is the fractional reduction in unexplained variation compared to
using the mean model) is the "adjusted" R-squared of the model, and
in a simple regression model it is given by the formula
![]() .
.
The factor of (n-1)/(n-2) in this equation is the same adjustment for
degrees of freedom that is made in calculating the standard error of the
regression. In fact, adjusted R-squared can be used to determine the standard
error of the regression from the sample standard deviation of Y in exactly the same
way that R-squared can be used to determine the sample standard deviation of
the errors as a fraction of the sample standard deviation of Y:
![]()
You can apply this equation without even
calculating the model coefficients or the actual errors!
In a multiple regression model with k independent variables
plus an intercept, the number of degrees of freedom for error is n-(k+1), and the formulas for the standard error of
the regression and adjusted R-squared remain the same except that the n-2 term is replaced by n-(k +1) .
It follows from the equation above that if
you fit simple regression models to the same sample of the same dependent
variable Y with different
choices of X as the independent
variable, then adjusted R-squared
necessarily goes up as the standard error of the regression goes down, and vice
versa. Hence, it is equivalent to say that your goal is to minimize the
standard error of the regression or to maximize adjusted R-squared through your
choice of X, other things being
equal. However, as I will keep saying, the standard error of the regression is
the real "bottom line" in your analysis: it measures the variations
in the data that are not explained by the model in real economic or physical
terms.
Adjusted R-squared can actually be negative
if X has no measurable
predictive value with respect to Y. In particular, if the correlation between X and Y is exactly zero, then
R-squared is exactly equal to zero, and adjusted R-squared is equal to 1 - (n-1)/(n-2), which is negative because the ratio (n-1)/(n-2) is greater than 1. If this is the case,
then the mean model is clearly a better choice than the regression model. Some
regression software will not even display a negative value for adjusted
R-squared and will just report it to be zero in that case. Return
to top of page.
Formulas for standard errors and confidence limits for
means and forecasts
The standard
error of the mean of Y for
a given value of
X is the
estimated standard deviation of the error in measuring the height of the
regression line at that location, given by the formula

This looks like a lot like the formula for
the standard error of the mean in the mean model: it is proportional to the
standard error of the regression and inversely proportional to the square root
of the sample size, so it gets steadily smaller as the sample size gets larger,
approaching zero in the limit even in the presence of a lot of noise. However,
in the regression model the standard error of the mean also depends to some
extent on the value of X,
so the term ![]() is
scaled up by a factor that is greater than 1 and is larger for values of X that are farther from
its mean, because there is relatively greater uncertainty about the true height
of the regression line for values of X that are farther from its historical mean value.
is
scaled up by a factor that is greater than 1 and is larger for values of X that are farther from
its mean, because there is relatively greater uncertainty about the true height
of the regression line for values of X that are farther from its historical mean value.
The standard
error for the forecast for Y for
a given value of
X is then
computed in exactly the same way as it was for the mean model:
![]()
In the regression model it is larger for values of X that are farther from
the mean--i.e., you expect to make bigger forecast errors when extrapolating
the regression line farther out into space--because SEmean(X) is larger for more extreme values of X. The standard error of the
forecast is not quite as sensitive to X in relative terms as is the standard
error of the mean, because of the presence of the noise term s2 under the square root sign. (Remember that s2 is the estimated variance of the noise in the data.) In fact, s is
usually much larger than SEmean(X) unless the data set is very small or X is very
extreme, so usually the standard error of the forecast is not too much larger
than the standard error of the regression.
Finally, confidence limits for
means and forecasts are calculated in the usual way, namely as the forecast
plus or minus the relevant standard error times the critical t-value for the
desired level of confidence and the number of degrees of freedom, where the
latter is n-2 for a simple regression model. For all but
the smallest sample sizes, a 95% confidence interval is approximately equal to
the point forecast plus-or-minus two standard errors, although there is nothing
particularly magical about the 95% level of confidence. You can choose your
own, or just report the standard error along with the point forecast.
Here are a couple of additional pictures that
illustrate the behavior of the standard-error-of-the-mean and the
standard-error-of-the-forecast in the special case of a simple regression
model. Because the standard error of the mean gets larger for extreme
(farther-from-the-mean) values of X, the confidence intervals for the mean (the height of the regression
line) widen noticeably at either end.
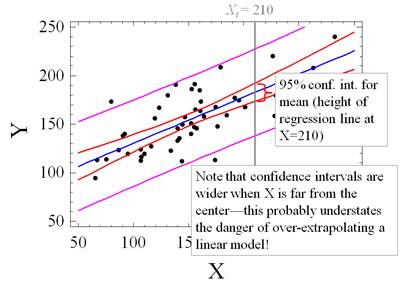
The confidence
intervals for predictions also get wider when X goes to extremes, but the effect is not quite as dramatic, because the
standard error of the regression (which is usually a bigger component of
forecast error) is a constant. Note that the inner set of confidence bands
widens more in relative terms at the far left and far right than does the outer
set of confidence bands.

But remember: the standard errors and confidence
bands that are calculated by the regression formulas are all based on the
assumption that the model is correct, i.e., that the data really is described
by the assumed linear equation with normally distributed errors. If the model
assumptions are not correct--e.g., if the wrong variables have been included or
important variables have been omitted or if there are non-normalities in the
errors or nonlinear relationships among the variables--then the predictions and
their standard errors and confidence limits may all be suspect. So, when we fit
regression models, we don′t just look at the printout of the model
coefficients. We look at various other statistics and charts that shed light on
the validity of the model assumptions. Return to top of page.
1. The coefficients and error measures for a
regression model are entirely determined by the following summary statistics: means, standard deviations and correlations
among the variables, and the sample size.
2. The correlation between Y and X , denoted by rXY, is equal to the average product of their standardized values, i.e., the average
of {the number of standard deviations by which Y deviates from its mean} times {the number of
standard deviations by which X
deviates from its mean}, using the population (rather than sample) standard
deviation in the calculation. This
statistic measures the strength of the linear relation between Y and X on a relative scale
of -1 to +1. The correlation
between Y and X is positive if they
tend to move in the same direction relative to their respective means and
negative if they tend to move in opposite directions, and it is zero if their
up-or-down movements with respect to their own means are statistically
independent.
3. The
slope coefficient in a simple regression of Y on X is the correlation between Y
and X multiplied by the ratio of their standard
deviations:
![]()
Either the population or sample standard deviation
(STDEV.S) can be used in this formula because they differ only by a
multiplicative factor.
4. In a simple regression model, the percentage of
variance "explained" by the model, which is called R-squared, is the
square of the correlation between Y and X. That
is, R-squared = rXY2, and that′s why
it′s called R-squared. This means that the sample standard deviation of
the errors is equal to {the square root of 1-minus-R-squared} times the sample
standard deviation of Y:
STDEV.S(errors) =
(SQRT(1 minus R-squared)) x STDEV.S(Y).
So, if you know the standard deviation of Y, and you know the
correlation between Y and X, you can figure out
what the standard deviation of the errors would be be if you regressed Y on X. However...
5. The sample standard deviation of the
errors is a downward-biased estimate
of the size of the true unexplained deviations in Y because it does not adjust for the additional
"degree of freedom" used up by estimating the slope coefficient. An unbiased estimate of the standard
deviation of the true errors is given by the standard error of the regression, denoted by s. In the special case
of a simple regression model, it is:
Standard error of
regression = STDEV.S(errors) x SQRT((n-1)/(n-2))
This is the real
bottom line,
because the standard deviations of the errors of all the forecasts and
coefficient estimates are directly proportional to it (if the model′s
assumptions are correct!!)
6. Adjusted
R-squared, which is obtained by adjusting R-squared for the degrees if freedom
for error in exactly the same way, is an unbiased estimate of the amount of
variance explained:
Adjusted R-squared = 1 - ((n-1)/(n-2)) x (1 -
R-squared).
For large values of n, there isn′t
much difference.
In a multiple regression model in which k is the number of
independent variables, the n-2 term that appears in
the formulas for the standard error of the regression and adjusted R-squared
merely becomes n-(k+1).
7. The important thing about adjusted
R-squared is that:
Standard error of the
regression = (SQRT(1 minus adjusted-R-squared)) x
STDEV.S(Y).
So, for models fitted to the same sample of
the same dependent variable, adjusted R-squared always goes up when the
standard error of the regression goes down.
A model
does not always improve when more variables are added: adjusted R-squared
can go down (even go negative) if irrelevant
variables are added.
8. The standard
error of a coefficient estimate is the estimated standard deviation of the
error in measuring it. Also, the estimated height of the regression line for a
given value of X
has its
own standard error, which is called the standard
error of the mean at X. All of these standard errors are proportional to the
standard error of the regression divided by the square root of the sample size.
So a greater amount of "noise" in the data (as measured by s) makes all the
estimates of means and coefficients proportionally less accurate, and a larger sample size makes all of them more accurate (4 times as much data reduces
all the standard errors by a factor of 2, etc.). However, more data will not
systematically reduce the standard error of the regression. Rather, the standard error of the regression will
merely become a more accurate estimate of the true standard deviation of the
noise.
9. The standard
error of the forecast for Y at
a given value of
X is the square root of the sum of squares of
the standard error of the regression and the standard error of the mean at X.
The
standard error of the mean is usually a lot smaller than the standard error of
the regression except when the sample size is very small and/or you are trying
to predict what will happen under very extreme conditions (which is dangerous),
so the standard error of the forecast is usually only slightly larger than the
standard error of the regression. (Recall that under the mean model, the
standard error of the mean is a constant. In a simple regression model, the
standard error of the mean depends on the value of X, and it is larger
for values of X
that are
farther from its own mean.)
10. Two-sided
confidence limits for coefficient estimates, means, and forecasts are all equal
to their point estimates plus-or-minus the appropriate critical t-value times
their respective standard errors. For a simple regression model, in which
two degrees of freedom are used up in estimating both the intercept and the
slope coefficient, the appropriate critical t-value is T.INV.2T(1 - C, n - 2) in
Excel, where C is the desired level of confidence and n is the sample size.
The usual default value for the confidence level is 95%, for which the critical
t-value is T.INV.2T(0.05, n - 2).
The
accompanying Excel file with
simple regression formulas shows how the calculations described above can
be done on a spreadsheet, including a comparison with output from RegressIt. For the case in which there are two or
more independent variables, a so-called multiple
regression model, the calculations are not too much harder if you are
familiar with how to do arithmetic with vectors and matrices. Here is an Excel
file with regression formulas in matrix form that illustrates this process. Return
to top of page.
Go on to next topic: example of a simple regression
model
