Three types of forecasts: estimation, validation, and the future

A good way to test the assumptions of a model and to realistically compare its forecasting performance against other models is to perform out-of-sample validation, which means to withhold some of the sample data from the model identification and estimation process, then use the model to make predictions for the hold-out data in order to see how accurate they are and to determine whether the statistics of their errors are similar to those that the model made within the sample of data that was fitted. In the Forecasting procedure in Statgraphics, you are given the option to specify a number of data points to hold out for validation and a number of forecasts to generate into the future. The data which are not held out are used to estimate the parameters of the model. The model is then tested on data in the validation period, and forecasts are generated beyond the end of the estimation and validation periods. For example, consider a hypothetical time series Y of which a sample of 100 observations is available, as shown in the chart below. Suppose that a random-walk-with-drift model (which is specified as an "ARIMA(0,1,0) with constant" model in Statgraphics) is fitted to this series. If the last 20 values are held out for validation and 12 forecasts for the future are generated, the results look like this:

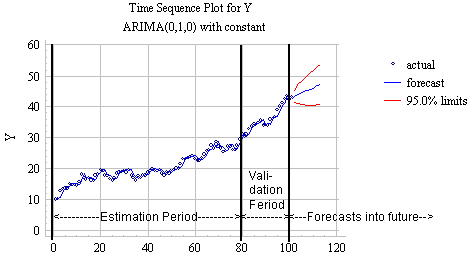
In general, the data in the estimation period are used to help select the model and to estimate its parameters. Forecasts made in this period are not completely "honest" because data on both sides of each observation are used to help determine the forecast. The one-step-ahead forecasts made in this period are usually called fitted values. (They are said to be "fitted" because our software estimates the parameters of the model so as to "fit" them as well as possible in a mean-squared-error sense.) The corresponding forecast errors are called residuals. The residual statistics (MSE, MAE, MAPE) may understate the magnitudes of the errors that will be made when the model is used to predict the future, because it is possible that the data have been overfitted--i.e, by relentlessly minimizing the mean squared error, the model may have inadvertently fitted some of the "noise" in the estimation period as well as the "signal." Overfitting is especially likely to occur when either (a) a model with a large number of parameters (e.g., a model using seasonal adjustment) has been fitted to a small sample of data and/or (b) the model has been selected from a large set of potential models precisely by minimizing the mean squared error in the estimation period (e.g., when stepwise or all-subsets regression has been used with a large set of potential regressors).

The data in the validation period are held out during parameter estimation, and if you are careful you will also withhold these values during the exploratory phase of analysis when you select your model. One-step-ahead forecasts made in this period are often called backtests. Ideally, these are "honest" forecasts and their error statistics are representative of errors that will be made in forecasting the future. However, if you test a great number of models and choose the model whose errors are smallest in the validation period, you may end up overfitting the data within the validation period as well as in the estimation period.

In Statgraphics, the statistics of the forecast errors in the validation period are reported alongside the statistics of the forecast errors in the estimation period, so that you can compare them. For example, the Analysis Summary report for the random walk model with drift looked like this:

Forecast model selected: ARIMA(0,1,0) with constant
Number of forecasts generated: 12
Number of periods withheld for validation: 20

            Estimation      Validation
Statistic   Period          Period
--------------------------------------------
MSE         0.886679        1.02186
MAE         0.762752        0.835759
MAPE        3.85985         2.263
ME          -0.00515478     0.381454
MPE         -0.0865215      1.00468

If the data have not been badly overfitted, the error measures in the validation period should be similar to those in the estimation period, although they are often at least slightly larger. Here we see that the MSE in the validation period is indeed slightly larger than in the estimation period: 1.02 versus 0.89.

Holding data out for validation purposes is probably the single most important diagnostic test of a model: it gives the best indication of the accuracy that can be expected when forecasting the future. If you have the luxury of large quantities of data, I recommend that you hold out at least 20% of your data for validation purposes. If you really have a lot of data, you might even try holding out 50%--i.e., select and fit the model to one-half of the data. then validate it on the other half. In the case of regression models, you can run this exercise both ways and compare coefficient estimates as well as error statistics between the first half and last half. Ideally these should be in general agreement as well. When you're ready to forecast the future in real time, you should of course use all the available data for estimation, so that the most recent data is used. Alas, it is difficult to properly validate a model if data is in short supply. For example, if you have only 20 data points, then you cannot afford to hold out very many for validation, and your sample size for the validation period may be too small to be a reliable indicator of future forecasting performance.

Forecasts into the future are "true" forecasts that are made for time periods beyond the end of the available data. For a model which is purely extrapolative in nature (i.e., which it forecasts a time series entirely from its own history), it is possible to extend the forecasts an arbitrary number of periods into the future by "bootstrapping" the model: first a one-period-ahead forecast is made, then the one-period-ahead forecast is treated as a data point and the model is cranked ahead to produce a two-period-ahead forecast, and so on as far as you wish.

Most forecasting software is capable of performing this kind of extrapolation automatically and also calculating confidence intervals for the forecasts. (The 95% confidence interval is roughly equal to the forecast plus-or-minus two times the estimated standard deviation of the forecast error at each period.) The confidence intervals typically widen as the forecast horizon increases, due to the expected build-up of error in the bootstrapping process. The rate at which the confidence intervals widen will in general be a function of the type of forecasting model selected. Models may differ in their assumptions about the intrinsic variability of the data, and these assumptions are not necessarily correct. Therefore, the model with the tightest confidence intervals is not always the best model: a bad model does not always know it is a bad model! For example, the linear trend model assumes that the data will vary randomly around a fixed trend line, and its confidence intervals therefore widen very little as the forecast horizon increases. (They only reason that they widen at all is because of uncertainty in the slope and intercept coefficients based on small samples of data.) As we have seen, this assumption is often inappropriate, and therefore the confidence intervals for the linear trend model are usually overly optimistic (i.e., too narrow).

The confidence intervals for the random walk model diverge in a pattern that is proportional to the square root of the forecast horizon (a sideways parabola). This "square root of time" rule follows from the fact that the variance of the errors in the random walk model grows linearly: the variance of the two-step-ahead forecast error is exactly twice the variance of the one-step-head forecast error, the variance of the three-step-ahead forecast error is exactly three times the variance of the one-step-ahead forecast error, and so on. After n steps into the future, the variance of the forecast error is n times the one-step-ahead error variance, and since the standard deviation of the forecast errors is the square root of the variance, the standard deviation of the n-step ahead forecast error is proportional to the square root of n for the random walk model.