Statistics
review and the simplest forecasting model: the sample mean (pdf)
Notes on the random
walk model (pdf)
Mean (constant) model
Linear trend model
Random walk model
Geometric random
walk model
Three types of forecasts: estimation, validation, and the
future
Geometric random walk model
Logarithm
transformations of stock price data: Previously we saw that a
random-walk-without-drift model was capable of describing a financial time
series with no long-term trend and relatively constant volatility in absolute
terms (at least over the long run). What if the series displays an overall exponential trend and increasing volatility in absolute terms?
For example, here is a plot of the monthly closing values of the S&P 500
stock index from January 1980 to November 2014, showing consistent exponential
growth in the early years followed by the two (three?) market bubbles.

If we take
the first difference (monthly change) of this series, we obtain a series that
shows much higher variance during periods when the level was high:

These two
pictures suggest that the growth rate and random fluctuations may be more
consistent over time in percentage terms than in absolute terms. We can
linearize the exponential growth in the original series, and also stabilize the
variance of the monthly changes, by applying a natural
logarithm transformation.
Here's what it yields:
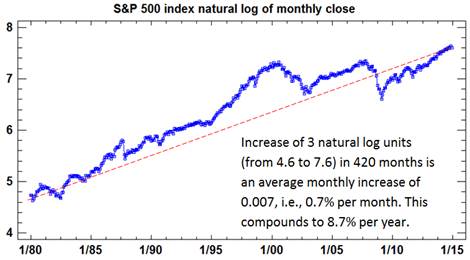
The growth
pattern now appears much more linear, although it has not been very consistent
in this wild-west era of epic bubbles and busts. As explained in the notes on the natural
log transformation, a trend measured in natural log units can be interpreted as
a trend measured in percentage terms, to a very high degree of approximation,
if it is on the order 5% or less per period. Here, a trend line has been hand-drawn
on the chart merely for visual reference, and it shows that the logged S&P
500 index has increased by about 3 units over the 420 months in the sample,
translating into an average monthly increase of 0.007, which can be interpreted
as 0.7% and which compounds to around 8.7% per year.
The
variance of the monthly changes also appears much more stable in log units, as
shown by a plot of the first difference of the logged series (its
"diff-log"):

The first
difference of the natural logarithm is essentially the percentage difference in the original series,
so what we have actually plotted here is the monthly percent return on
the S&P500 index (ex-dividends), and it generally falls in the range
between plus-and-minus 0.05, i.e., 5%. Its standard deviation is 0.044,
i.e., 4.4%.
Finally,
let's check to see whether the diff-logged values are statistically
independent. Here is a plot of
their autocorrelations and 95% confidence bands around zero:
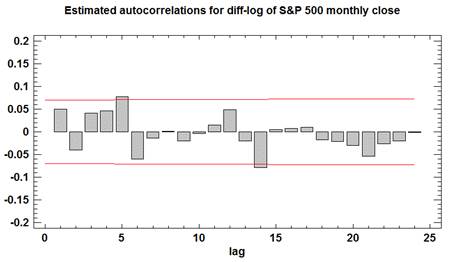
The
autocorrelations of the diff-logged series do not appear significant and do not
show any systematic pattern, from which we can conclude that the logged S&P 500 monthly closing
values can be reasonably described as a
random walk with drift.
When the
random-walk-with-drift model is fitted to the logged data, the point forecasts
and their 95% confidence limits for the next 3 years look like this:

The point
forecasts follow a straight line and the confidence bands for long term
forecasts have the characteristic sideways-parabola shape and are symmetric
around the point forecasts. The
drift has been estimated from the data sample in this case. This does not mean that a trend line has
been fitted by the usual regression method. Rather, it is as if a straight line was
drawn between the first and last data points and extrapolated from there. (That is the mathematical consequence of
applying the mean model to the diff-logged values: within the given data sample, the average
change from one period to the next is just the total change divided by the
number of time periods over which it occurred.) The dashed line on the above
plot has been added to emphasize this fact. It is apparent that this method of
estimating the drift could have yielded very different results if a different
amount of history had been used.
For example, if the starting point had been the peak of the dot-com
bubble, in August 2000, an extrapolation of a straight line through the first
and last points would have looked like this instead:

The level
of the series only increased by 0.28 log units over these 172 months (from 7.32
to 7.6), translating into 0.00165 per month (i.e., 0.165% per month), which
compounds to only 2% per year! On
the other hand, if you measure the growth rate over the 70-month period
starting from the bottom of the housing bust in March 2009, you get a much more
optimistic estimate of 19% per year:

This is why
it can be dangerous to estimate the average rate of return to be expected in
the future (let alone anticipate short-term changes in direction), by fitting
straight lines to finite samples of data.
Geometric
random walk model:
Application of the random walk model
to the logged series implies that the forecast for the next month's value of
the original series will equal the previous month's value plus a constant percentage
increase. To see this, note that the random walk forecast for LN(Y) is given by
the equation:
LN(Ŷt) = LN(Yt-1)
+ α
where the
constant term (alpha) is the average monthly change in LN(Y), which is
approximately the average monthly percentage change in Y. For the
S&P 500 series, alpha is equal to 0.007, representing an average monthly
increase of 0.7%. Exponentiating both sides of the preceding equation, and
using the fact that EXP(x) is approximately equal to 1+x for small x, we
obtain:
Ŷt = Yt-1 X EXP(α) ≈ Yt-1 X (1 + α)
This
forecasting model is known as a geometric random walk model, and it is
the default model commonly used for stock market data. (In Statgraphics, you
specify this model as a random-walk-with-growth model in combination with a
natural log transformation. On the Model
Specification panel in the user-specified forecasting procedure, just click
the "Random walk" button for the model type and the "Natural
log" button for the math adjustment, and check the "Constant"
box to incorporate constant growth.) Here's a plot of the forecasts produced by
this model for the S&P 500 series:

This
picture is the same as the previous one except for the unlogging of the
vertical scale. The forecasts grow
at a rate equal to the average monthly increase within the sample, which is
0.7%, translating into 8.7% per year as noted earlier. In unlogged units, the 95% confidence
limits for long-term forecasts are noticeably asymmetric, being wider on the
high side.
For a much more
complete discussion of the geometric random walk model, see the "Notes
on the random walk model" handout.
A
"random walk down Wall Street": The fact
that stock prices behave at least approximately like a (geometric) random walk
is the most striking empirical fact about financial markets. But is it or
isn't it a true random walk? If it is, then stock prices are inherently
unpredictable except in terms of long-run-average risk and return. The
best you can hope to do is to correctly estimate the average returns and
volatilities of stocks, along with their correlations, and use these statistics
to determine efficient portfolios that achieve a desired risk-return
tradeoff. You can't hope to beat the market by microanalyzing patterns in
stock price movements--you might as well buy-and-hold an efficient portfolio.
The random
walk hypothesis was first formalized by the French mathematician (and stock
analyst) Louis Bachelier in 1900, and in the past century it has been
exhaustively studied and debated. The intuition for the random walk
hypothesis is a variation on the economist's classical efficiency argument,
which holds that a $100 bill will never be found lying on the sidewalk because
someone else would have picked it up first. If it could be predicted from
publicly available information that an abnormally large positive stock return
will occur tomorrow, then the price of the stock should already have gone up
today, in which case the anticipated return would already have been realized,
and tomorrow's return should be normal after all. What is not quite so
obvious is why the volatility of stock returns should be approximately
constant, as the basic random walk model assumes. (It is not exactly
constant in practice, but it does tend to revert to an average volatility
level over the long term.) Evidently investors naturally think in terms
of percentage changes when it comes to financial asset prices, so that
similar informational events (earnings reports, changes in interest rates or
inflation, etc.) tend to lead to similar percentage changes in stock prices at
different points in time.
Nowadays,
three different forms of the random walk hypothesis are commonly
distinguished. The weak form holds that future stock returns
cannot be predicted from past returns (except in the long-run-average sense),
which rules out so-called "technical analysis" and stock-trading
strategies such as "filter rules" in which buying and selling are
triggered when stock prices hit target levels determined by recent highs and
lows. The semi-strong form holds that future stock returns cannot
be predicted from past returns even together with other publicly available
information such as corporate statements and analyst reports, which rules
out the possibility that actively managed mutual funds will outperform a broad
market index (except by luck). The strong form holds that stock
returns cannot be predicted from any available information, even inside
information not available to the general public, which rules out excess profits
from insider trading. The strong form is obviously too strong to be
plausible: prices are moved by information (as well as by animal spirits,
etc.), and those who are able to trade on the information first, before
prices have moved very much, should expect to profit. The
general consensus seems to be that the truth lies somewhere between the
semi-strong and the strong form: technical analysis has not been
validated in controlled studies (although it still has passionate defenders),
and actively managed mutual funds generally do not consistently outperform the
market index, although inside information does create opportunities for
(illegal) excess profits.
On
reflection, it is intuitively reasonable that stock prices should follow a
random walk approximately, but not exactly. Small-scale patterns in stock
prices should always be emerging and then dissipating as information is
received by the most alert and savvy market participants, who then trade on it
until the rest of the market catches on. However, because of market
frictions (transaction costs such as bid-ask spreads, brokerage fees, taxes,
etc.), these patterns will usually be too small for the typical market observer
to profit from. For most practical purposes, for most people, it is
a random walk. This is not to say the market moves up or down for
purely random reasons. Looking backward, it is usually possible to
identify sound economic reasons for particular historical movements of stock
prices (notwithstanding the occasional speculative bubble like the dot-com
craze of the late 1990's). But looking forward, expectations of
future returns are already factored into today's prices, just so that future
returns will be average if today's expectations are exactly met. To the
extent that future returns deviate from the average, it will be due to the
occurrence of unanticipated events, which by definition are random deviations
from today's expectations.
The debate
between "technicians" and "random-walkers" has taken a new
turn with the emergence of behavioral finance as a lively field of study.
Behavioral finance studies markets from the perspective that investors are not
rational in the expected-utility-maximizing sense of classical finance theory,
as laboratory experiments have convincingly shown, which suggests that
psychological theories might be helpful in explaining some of the puzzles that
are observed in markets. On this view, reading stock charts might help to
anticipate the patterns that other people are likely to read into stock
charts. (The idea that markets are better predicted by psychological
analysis than by rational economic calculations, analogous to guessing the
winner of a beauty contest, actually dates back to John Maynard Keynes.)
But on the other hand, behavioral research has also convincingly demonstrated
that people tend to misperceive random sequences as non-random--the so-called
"hot hand in basketball" phenomenon. For more discussion of the
random walk hypothesis and its implications for investing, see A Random
Walk Down Wall Street by Burton Malkiel. (The latest
edition was published in 2012.) (Return to top of
page.)
More
general random walk forecasting models: For purposes of time series
forecasting, three versions of the random walk model can also be
distinguished. RW model 1 (the basic geometric random walk model illustrated
above and implementable in Statgraphics) assumes that stock returns in
different periods are statistically independent (uncorrelated) and also identically
distributed--i.e. the market has constant volatility. The only
parameters to estimate are the average period-to-period return (the constant
term in the ARIMA(0,1,0) model) and the volatility (the so-called white
noise standard deviation in the ARIMA(0,1,0) model, which is just ARIMA
jargon for root-mean-squared error). RW model 2 assumes that
returns in different periods are statistically independent but not
identically distributed--for example, the volatility might change
deterministically over time or it might depend on the current price level,
which would require more parameters to specify. RW model 3 assumes
that returns in different periods are uncorrelated but not
otherwise independent--e.g., the volatility in one period might depend on the
volatility in recent periods. The ARCH (autoregressive conditional
heteroscedasticity) and GARCH (generalized ARCH) models assume that the
local volatility follows an autoregressive process, which is
characterized by sudden jumps in volatility with a slow reversion to an average
volatility. The autoregressive behavior of volatility is clearly evident
in plots of returns over long periods, particularly high-frequency returns such
as daily returns. Robert Engle received the Nobel Prize in
Economics in 2003 for developing the ARCH model, and it is commonly used by
econometricians, although it is not available in Statgraphics. Subjective
estimates of time-varying volatilities are also revealed by prices of
derivative securities such as options: the "implied volatility"
of a stock price at a given point in time can be determined from stock options
prices using an options pricing model such as the Black-Scholes model.
What
does the empirical data show? Besides time-varying volatility, there is
some evidence for positive autocorrelation ("momentum") in some
stock price data, particularly at high frequencies (e.g. daily).
The history of daily returns on the S&P500 index and the Dow Jones
Industrial Average over the last 50 years shows a slight but technically
significant positive autocorrelation at lag 1, although this pattern seems to have
faded in recent decades. (Perhaps it self-destructed?) Other
patterns have also been observed to arise in some decades and fade away in
others. The behavior of the CRSP index (a common benchmark for
econometricians) is even more remarkable: daily returns on the CRSP
value-weighted index and equal-weighted index displayed lag-1 autocorrelations
in the range of 30% to over 40% over the period 1962-1978, and slightly less
over the larger period 1962-1994. This is remarkable not only for the
very large magnitude of the autocorrelations but also for the fact that returns
on individual stocks in the sample typically displayed no autocorrelation.
One explanation of this puzzle is that there appear to be significant cross-correlations
(also called "cross-auto-correlations") between different
segments of the market--e.g., some stocks tend to lead or lag others, as though
information diffuses across the market from one day to the next, even though
individually they behave like random walks. Thus, for example, stocks A and
B could both have zero autocorrelation at lag 1, but A could have a significant
lag-1 cross-correlation with stock B, and a portfolio formed of A plus B could
therefore have significant autocorrelation at lag 1. The question remains
whether this pattern is (or was) significant enough to present opportunities
for excess profits. Transaction costs make it difficult to profit from
trades in large numbers of stocks at once, unless the index is itself a traded
asset. If there were an asset pegged to the same CRSP index used in these
studies, the autocorrelation pattern might have been expected to
self-destruct. So, there are some predictable patterns in stock
prices (particularly at the aggregate level, and seen in hindsight), but the
returns on individual assets that can be traded with low transaction costs are
in reasonable agreement with RW model 3, if not one of the more restrictive
models. For more information (at a much higher technical level), see The
Econometrics of Financial Markets by John Campbell, Andrew Lo, and A. Craig
MacKinlay. (Return
to top of page.)
