Receiver Operating Characteristic¶
In [101]:
suppressPackageStartupMessages(library(tidyverse))
Logistic regression concept¶
In logistic regression, we want to relate some predictor variable (e..g gene expression value) to the probability of a binary outcome. We would like a linear model since that is mathematically and computationally tractable, but run into the issue that probabilities are restricted to [0,1]. Logistic regression solves this by transforming the output of a linear model into the [0, 1] range.
In [102]:
n <- 50
x <- seq(-4, 4, length.out = n)
a = 0
b = 1
lx <- a + b*x
px <- exp(lx)/(1 + exp(lx))
y <- rbinom(n, 1, px)
df <- data.frame(y=y, x=x, lx=lx, px=px)
In [103]:
options(repr.plot.width=4, repr.plot.height=3)
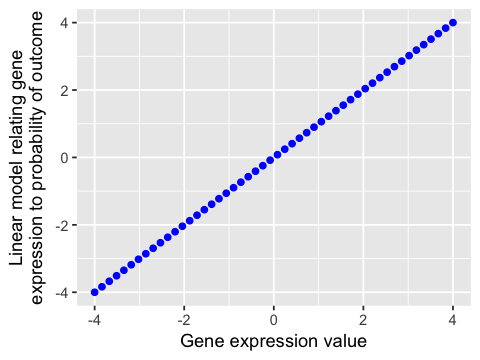
A linear model cannot be directly interpreted as a probability¶
In [104]:
ggplot(df, aes(x=x, y=lx)) +
geom_point(color='blue') +
labs(x="Gene expression value",
y="Linear model relating gene\nexpression to probability of outcome")
Data type cannot be displayed:
In [105]:
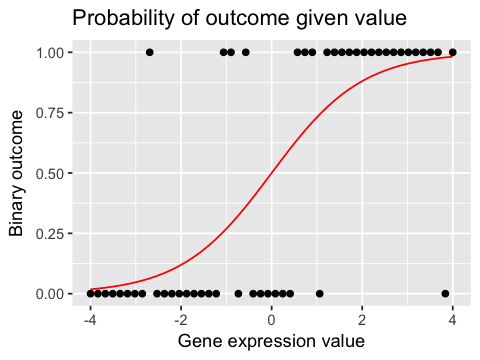
ggplot(df, aes(x=x, y=y)) +
geom_point() +
geom_line(aes(y=px), color='red') +
labs(x="Gene expression value", y="Binary outcome",
title="Probability of outcome given value")
Data type cannot be displayed:
Simulation from logistic model¶
In [106]:
sim.binomial <- function(n, b0, b1, b2, b3) {
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
lx <- b0 + b1 * x1 + b2 * x2 + b3 * x3
px <- exp(lx)/(1 + exp(lx))
y <- rbinom(n, 1, px)
data.frame(y, px, x1, x2, x3)
}
LOOCV¶
In [107]:
set.seed(31219)
data <- sim.binomial(100, 0.1, 0, 1, 0)
In [108]:
head(data)
| y | px | x1 | x2 | x3 |
|---|---|---|---|---|
| 0 | 0.5830298 | 1.2472628 | 0.23522348 | 1.4787281 |
| 1 | 0.4546145 | 0.5804904 | -0.28204321 | -0.8217013 |
| 1 | 0.5417889 | 0.3065363 | 0.06754626 | 1.3946841 |
| 1 | 0.8080377 | 0.4604304 | 1.33730956 | 0.6502840 |
| 0 | 0.5436883 | 1.2094387 | 0.07519995 | 0.6585957 |
| 1 | 0.4011430 | 0.2338796 | -0.50070506 | -0.8225897 |
In [119]:
n <- nrow(data)
pred <- numeric(n)
for (i in 1:n) {
train <- data[-i,]
test <- data[i,]
model <- glm(y ~ x1 + x2 + x3, data=train, family="binomial")
pred[i] <- predict(model, test, type="response")
}
yhat <- ifelse(pred < 0.5, 0, 1)
preddat <- data.frame(probhat=pred, yhat=yhat, y=data$y)
Confusion matrix¶
In [120]:
suppressPackageStartupMessages(library(caret))
In [123]:
tbl <- table(yhat, data$y)
confusionMatrix(tbl)
Confusion Matrix and Statistics
yhat 0 1
0 31 26
1 21 22
Accuracy : 0.53
95% CI : (0.4276, 0.6306)
No Information Rate : 0.52
P-Value [Acc > NIR] : 0.4607
Kappa : 0.0547
Mcnemar's Test P-Value : 0.5596
Sensitivity : 0.5962
Specificity : 0.4583
Pos Pred Value : 0.5439
Neg Pred Value : 0.5116
Prevalence : 0.5200
Detection Rate : 0.3100
Detection Prevalence : 0.5700
Balanced Accuracy : 0.5272
'Positive' Class : 0
ROC and AUC¶
In [124]:
suppressPackageStartupMessages(library(ROCR))
Helper functions¶
In [125]:
ROC <- function(preddat, mlab = "probhat", ylab = "y") {
m <- preddat[[mlab]]
y <- preddat[[ylab]]
performance(prediction(m, y), measure = "tpr", x.measure = "fpr")
}
AUC <- function(preddat, mlab = "probhat", ylab = "y") {
m <- preddat[[mlab]]
y <- preddat[[ylab]]
performance(prediction(m, y), "auc")@y.values[[1]]
}
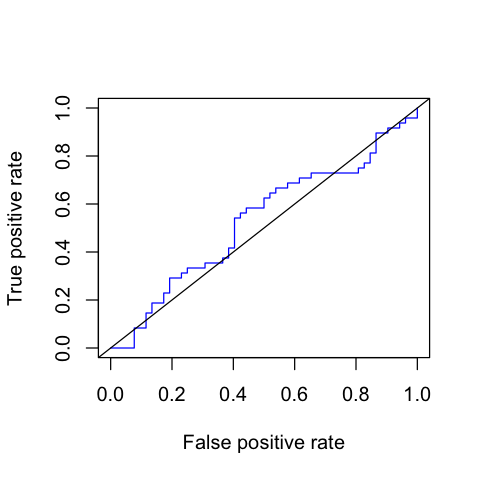
Calculate and plot ROC and AUC¶
In [126]:
my.roc <- ROC(preddat)
my.auc <- AUC(preddat)
In [127]:
my.auc
0.530048076923077
In [128]:
options(repr.plot.width=4, repr.plot.height=4)
In [129]:
plot(my.roc, col = "blue")
abline(0, 1)
Resubstitution ROC¶
In [134]:
model.1 <- glm(y ~ x1 + x2 + x3, data=data, family="binomial")
pred.1 <- predict(model.1, type="response")
yhat.1 <- ifelse(pred.1 < 0.5, 0, 1)
preddat.1 <- data.frame(probhat=pred.1, yhat=yhat.1, y=data$y)
In [136]:
rs.roc <- ROC(preddat.1)
rs.auc <- AUC(preddat.1)
In [137]:
rs.auc
0.616987179487179
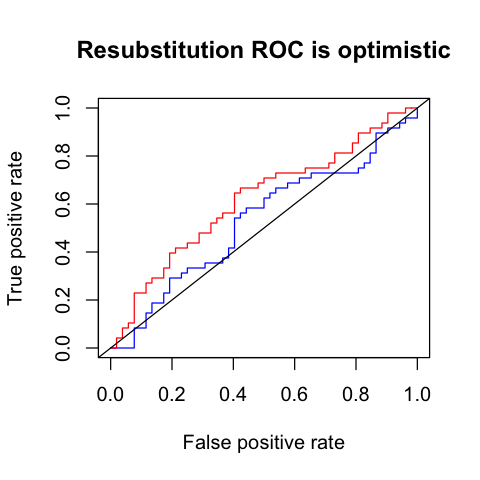
In [144]:
plot(my.roc, col = "blue", main="Resubstitution ROC is optimistic")
plot(rs.roc, col = "red", add=TRUE)
abline(0, 1)