Seasonal differencing

Seasonal difference (season-to-season change)
First difference of seasonal difference

The seasonal difference of a time series is the series of changes from one season to the next. For monthly data, in which there are 12 periods in a season, the seasonal difference of Y at period t is Y(t)-Y(t-12). In Statgraphics, the seasonal difference of Y with a seasonal period of 12 is expressed as SDIFF(Y,12), although you should not often need to use this expression: seasonal differencing, like nonseasonal differencing, can be performed as an analysis option within the time series procedures. If the seasonal difference of Y is "pure noise" (constant variance, no autocorrelation, etc.), then Y is described by a seasonal random walk model: each value is a random step away from the value that occurred exactly one season ago.

Seasonal differencing is a crude form of additive seasonal adjustment: the "index" which is subtracted from each value of the time series is simply the value that was observed in the same season one year earlier. Seasonal differencing therefore usually removes the gross features of seasonality from a series, as well as most of the trend. Here is a plot of the seasonal difference of AUTOSALE/CPI, the deflated auto sales series. Notice that little remains of the original seasonal pattern or trend, although it now looks a bit like a random walk rather than pure noise.

(Return to top of page.)

First difference of seasonal difference: In the preceding two graphs, we see that the first difference of AUTOSALE/CPI is far from random (it is still strongly seasonal), and the seasonal difference is far from stationary (it resembles a random walk). In this case, it appears that both kinds of differencing are needed to render the series stationary and to account for the gross pattern of seasonality. The first difference of the seasonal difference of a monthly time series Y at period t is equal to (Y(t) - Y(t-12)) - (Y(t-1) - Y(t-13)). Equivalently, it is equal to (Y(t) - Y(t-1)) - (Y(t-12) - Y(t-13)). This is the amount by which the change from the previous period to the current period is different from the change that was observed exactly one year earlier. Thus, for example, the first difference of the seasonal difference in September 1995 is equal to the August-to-September change in 1995 minus the August-to-September change in 1994. If the first difference of the seasonal difference of Y is pure noise, then Y is described by a seasonal random trend model.

In Statgraphics, the first difference of the seasonal difference of Y is expressed as DIFF(SDIFF(Y,12)), although, as noted above, you shouldn't need to use this expression very often. (Use the "analysis options" to perform all the necessary differencing inside the time series procedures.) Here is a plot of the first difference of the seasonal difference of AUTOSALE/CPI. Note that it now appears stationary without obvious signs of seasonality. (We should look at an autocorrelation plot to be sure that no seasonal pattern remains, but at least the gross seasonal pattern has been eliminated.)

(Return to top of page.)

The following spreadsheet shows how the seasonal difference and first difference of the seasonal difference are calculated in this example:

Seasonal random walk model

If the seasonal difference (i.e., the season-to-season change) of a time series looks like stationary noise, this suggests that the mean (constant) forecasting model should be applied to the seasonal difference. For monthly data, whose seasonal period is 12, the seasonal difference at period t is Y(t)-Y(t-12). Applying the mean model to this series yields the equation:

Y(t) - Y(t-12) =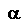

...where alpha is the the mean of the seasonal difference--i.e., the average annual trend in the data. Rearranging terms to put Y(t) on the left, we obtain:

Y(t) = Y(t-12) +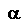

This forecasting model will be called the seasonal random walk model, because it assumes that each season's values form an independent random walk. Thus, the model assumes that September's 's value this year is a random step away from September's value last year, October's value this year is a random step away from October's value last year, etc., and the mean value of every step is equal to the same constant (denoted here as alpha). That is,

Y(Sep'96) = Y(Sep'95) +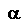

Y(Oct'96) = Y(Oct'95) +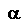

and so on. Notice that the forecast for Sep'96 ignores all data after Sep'95--i.e., it is based entirely on what happened exactly one year ago.

A seasonal random walk model is a special case of an ARIMA model in which there is one order of seasonal differencing, a constant term, and no other parameters--i.e., an "ARIMA(0,0,0)x(0,1,0) model with constant." To specify a seasonal random walk model in Statgraphics, choose ARIMA as the model type and use the following settings:

Differencing: Nonseasonal Order = 0, Seasonal Order = 1
AR, MA, SAR, SMA = 0
Constant = ON

The seasonal difference of the deflated auto sales data (AUTOSALE/CPI) does not quite look like stationary noise: it is rather highly correlated. If we fit the seasonal random walk model anyway (using the ARIMA option in Statgraphics), we obtain the following forecast plot:

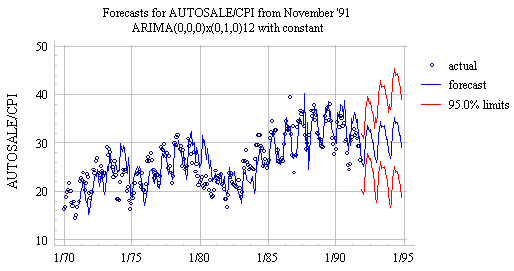
The distinctive feature of the forecasts produced by this model is that future seasonal cycles are predicted to have exactly the same shape as the most recently completed seasonal cycle, and the trend in the forecasts equals the average trend calculated over the whole history of the time series. If you look closely at the plot, you will notice that the model does not respond very quickly to cyclical upturns and downturns in the data: it is always looking exactly one year behind and assuming that the current trend equals the average trend, so that when the trend takes a cyclical upward or downward turn, the forecasts may miss badly in the same direction for many months in a row. Thus, the one-step-ahead forecast errors typically show positive autocorrelation. However, the long-term forecasts beyond the end of the sample appear reasonable insofar as they assume that the average trend in the past will eventually prevail again in the future.

Another distinctive feature of the seasonal random walk model is that it is relatively stable in the presence of sudden changes in the data--indeed, it doesn't even notice them for 12 months! For example, the previous plot shows long-term forecasts produced from time origin November 1991, at the end of a downward cycle. A few months later, the data begins to trend upward, but the long-term forecasts produced by the seasonal random walk model look much the same as before:

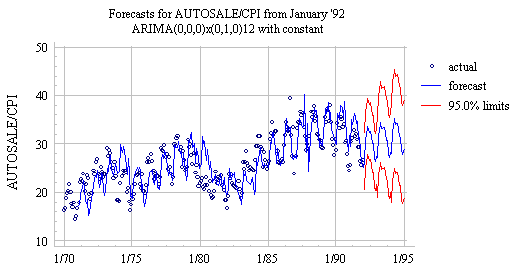
The positive autocorrelation in the errors of the seasonal random walk model can be reduced by adding a lag-1 autoregressive ("AR(1)") term to the forecasting equation. (In Statgraphics, you would do this by additionally setting AR=1). This yields an "ARIMA(1,0,0)x(0,1,0) model with constant," and its performance on the deflated auto sales series (from time origin November 1991) is shown here:

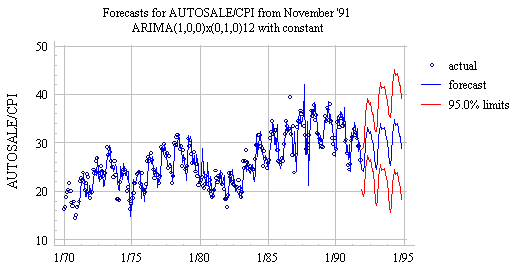
Notice the much quicker reponse to cyclical turning points. The in-sample RMSE for this model is only 2.05, versus 2.98 for the seasonal random walk model without the AR(1) term. (Return to top of page.)

Go to next topic: seasonal random trend model

Seasonal random trend model

Often a time series which has a strong seasonal pattern is not satisfactorily stationarized by a seasonal difference alone, and hence the seasonal random walk model (which predicts the seasonal difference to be constant) will not give a good fit. For example, the seasonal difference of the deflated auto sales series looks more like a random walk than a stationary noise pattern. However, if we look at the first difference of the seasonal difference of deflated auto sales, we see a pattern that looks more-or-less like stationary noise with a mean value of zero:

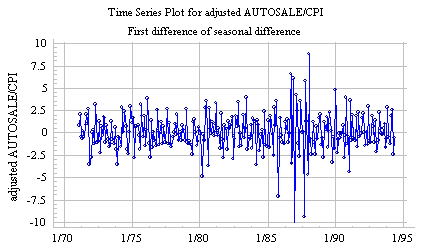
(Even if the mean value of a twice-differenced series is not exactly zero, we normally assume it is zero for forecasting purposes: otherwise we would be assuming a trend-in-the-trend, which would be dangerous to extrapolate very far.)

For monthly data, whose seasonal period is 12, the first difference of the seasonal difference at period t is (Y(t) - Y(t-12)) - (Y(t-1) - Y(t-13). Applying the zero-mean forecasting model to this series yields the equation:

(Y(t) - Y(t-12)) - (Y(t-1) - Y(t-13)) = 0

Rearranging terms to put Y(t) by itself on the left, we obtain:

Y(t) = Y(t-1) + Y(t-12) - Y(t-13)

For example, if it is now September '96 and we are using this equation to predict the value of Y in October '96, we would compute:

Y(Oct'96) = Y(Sep'96) + (Y(Oct'95) - Y(Sep'95)).

In other words, October's forecast equals September's value plus the September-to-October change observed last year. Equivalently, we can rewrite this as:

Y(Oct'96) = Y(Oct'95) + (Y(Sep'96) - Y(Sep'95)),

which says that October's forecast equals last October's value plus the year-to-year change we observed last month. (These preceding two equations are mathematically identical: we've just rearranged terms on the right-hand-side.)

This forecasting model will be called the seasonal random trend model, because it assumes that the seasonal trend (difference) observed this month is a random step away from the trend that was observed last month, where the steps are assumed to have mean zero. To see this, rewrite the equation in terms of seasonal differences:

Y(t) - Y(t-12)) = Y(t-1) - Y(t-13)

In other words, the expected seasonal difference this month is the same as the seasonal difference observed last month. Now compare this behavior with that of the seasonal random walk model: the seasonal random walk model assumes that the expected values of all future seasonal differences are equal to the average seasonal difference calculated over the whole history of the time series. In contrast, the seasonal random trend model assumes that the expected values of all future seasonal differences are equal to the most recently observed seasonal difference. Moreover, the seasonal random trend model assumes that the actual seasonal differences will be undergoing a zero-growth random walk--rather than fluctuating around some constant mean value--so their values will become very uncertain in the distant future.

The seasonal random walk model and the seasonal random trend model both predict that next year's seasonal cycle will have exactly the same shape (i.e., the same relative month-to-month changes) as this year's seasonal cycle. The difference between them is in their trend projections: the seasonal random walk model assumes that the future trend will equal the average year-to-year trend observed in the past, whereas the seasonal random trend model assumes that the future trend will equal the most recent year-to-year trend.

Returning to our example, if our last recorded value was for September '96, the seasonal random trend model will predict October's value to satisfy Y(Oct'96) - Y(Oct'95) = Y(Sep'96) - Y(Sep'95). If we then bootstrap the model one month into the future to predict November's value, the model will predict that Y(Nov'96) - Y(Nov'95) = Y(Oct'96) - Y(Oct'95) ...but this is exactly equal to Y(Sep'96) - Y(Sep'95) again, because the October '96 forecast must be used in place of an actual value. Thus, all future seasonal differences, as predicted from time origin September '96, will be identical to the September-to-September difference.

The seasonal random trend model is a special case of an ARIMA model in which there is one order of non-seasonal differencing, one order of seasonal differencing, and no constant or other parameters--i.e., an "ARIMA(0,1,0)x(0,1,0) model." In Statgraphics, you would specify a seasonal random trend model by choosing ARIMA as the model type and then selecting:

Differencing: Nonseasonal Order = 1, Seasonal Order = 1
AR, MA, SAR, SMA = 0
Constant = off

If we apply the seasonal random trend model to the deflated auto sales data, using data up to November '91, we obtain the following picture:

Notice that the one-step-ahead predictions (up to November '91) respond very quickly to cyclical upturns and downturns in the data, unlike those of the seasonal random walk model. Also notice that the predictions for future seasonal cycles have exactly the same shape as the last observed seasonal cycle (the one ending in November '91). However, the long-term forecasts march off with a downward trend equal to the downward trend that was observed from November '90 to November '91. The confidence limits for the long-term forecasts also diverge very rapidly because of the assumption that the actual future trend will be randomly changing.

If we recompute the forecasts using data up to January '92, we see a very different picture in the long-term forecasts:

The upward trend between January '91 and January '92 now causes the long-term forecasts to shoot off upward! Thus, we see that the seasonal random trend model is much more responsive than the seasonal random walk model to sudden shifts in the data. This serves it well when forecasting one period ahead, but renders it rather unstable for purposes of forecasting many periods ahead.

If you are thinking at this point that it probably would be better to do some amount of smoothing when estimating the seasonal pattern and/or the long-term trend in the forecasts, you are right. (By "smoothing" I mean that you might want to average over the last few season's data when estimating the seasonal pattern and/or the trend.) You can smooth the trend estimate by adding MA=1 to the parameter specifications, and you can smooth the estimate of the seasonal pattern by setting SMA=1. Adding both of these terms will yield an "ARIMA(0,1,1)x(0,1,1) model," which is probably the most commonly used ARIMA model for seasonal data. (For the technically curious, setting MA=1 adds a multiple of the one-month-prior forecast error to the right-hand-side of the forecasting equation, while setting SMA=1 adds a multiple of the 12-month-prior error, and adding both terms together also causes a multiple of the 13-month-prior error to be included. The resulting model is a kind of "seasonal linear exponential smoothing.") The forecasts generated by this model from time origin November '91 indeed show a smoother seasonal pattern, a more conservative trend estimate, and narrower confidence intervals:

The preceding qualitative observations are confirmed by the model comparison report for the seasonal random walk, seasonal random trend, and more elaborate ARIMA models fitted to the deflated auto sales data. The seasonal random trend model outperforms the seasonal random walk model within the estimation and validation periods (i.e., for all one-step-ahead forecasts), and the more elaborate models with additional ARIMA parameters improve on the simpler models without those parameters. (Return to top of page.)

Seasonal ARIMA models

Outline of seasonal ARIMA modeling
Example: AUTOSALE series revisited
The oft-used ARIMA(0,1,1)x(0,1,1) model: SRT model plus MA(1) and SMA(1) terms
The ARIMA(1,0,0)x(0,1,0) model with constant: SRW model plus AR(1) term
An improved version: ARIMA(1,0,1)x(0,1,1) with constant
Seasonal ARIMA versus exponential smoothing and seasonal adjustment
What are the tradeoffs among the various seasonal models?
To log or not to log?

Outline of seasonal ARIMA modeling:

The seasonal part of an ARIMA model has the same structure as the non-seasonal part: it may have an AR factor, an MA factor, and/or an order of differencing. In the seasonal part of the model, all of these factors operate across multiples of lag s (the number of periods in a season).
A seasonal ARIMA model is classified as an ARIMA(p,d,q)x(P,D,Q) model, where P=number of seasonal autoregressive (SAR) terms, D=number of seasonal differences, Q=number of seasonal moving average (SMA) terms
In identifying a seasonal model, the first step is to determine whether or not a seasonal difference is needed, in addition to or perhaps instead of a non-seasonal difference. You should look at time series plots and ACF and PACF plots for all possible combinations of 0 or 1 non-seasonal difference and 0 or 1 seasonal difference. Caution: don't EVER use more than ONE seasonal difference, nor more than TWO total differences (seasonal and non-seasonal combined).
If the seasonal pattern is both strong and stable over time (e.g., high in the Summer and low in the Winter, or vice versa), then you probably should use a seasonal difference regardless of whether you use a non-seasonal difference, since this will prevent the seasonal pattern from "dying out" in the long-term forecasts. Let's add this to our list of rules for identifying models

Rule 12: If the series has a strong and consistent seasonal pattern, then you should use an order of seasonal differencing--but never use more than one order of seasonal differencing or more than 2 orders of total differencing (seasonal+nonseasonal).
The signature of pure SAR or pure SMA behavior is similar to the signature of pure AR or pure MA behavior, except that the pattern appears across multiples of lag s in the ACF and PACF.
For example, a pure SAR(1) process has spikes in the ACF at lags s, 2s, 3s, etc., while the PACF cuts off after lag s.
Conversely, a pure SMA(1) process has spikes in the PACF at lags s, 2s, 3s, etc., while the ACF cuts off after lag s.
An SAR signature usually occurs when the autocorrelation at the seasonal period is positive, whereas an SMA signature usually occurs when the seasonal autocorrelation is negative, hence:

Rule 13: If the autocorrelation at the seasonal period is positive, consider adding an SAR term to the model. If the autocorrelation at the seasonal period is negative, consider adding an SMA term to the model. Do not mix SAR and SMA terms in the same model, and avoid using more than one of either kind.
Usually an SAR(1) or SMA(1) term is sufficient. You will rarely encounter a genuine SAR(2) or SMA(2) process, and even more rarely have enough data to estimate 2 or more seasonal coefficients without the estimation algorithm getting into a "feedback loop."
Although a seasonal ARIMA model seems to have only a few parameters, remember that backforecasting requires the estimation of one or two seasons' worth of implicit parameters to initialize it. Therefore, you should have at least 4 or 5 seasons of data to fit a seasonal ARIMA model.
Probably the most commonly used seasonal ARIMA model is the (0,1,1)x(0,1,1) model--i.e., an MA(1)xSMA(1) model with both a seasonal and a non-seasonal difference. This is essentially a "seasonal exponential smoothing" model.
When seasonal ARIMA models are fitted to logged data, they are capable of tracking a multiplicative seasonal pattern.

Example: AUTOSALE series revisited

Recall that we previously forecast the retail auto sales series by using a combination of deflation, seasonal adjustment and exponential smoothing. Let's now try fitting the same series with seasonal ARIMA models. As before we will work with deflated auto sales--i.e., we will use the series AUTOSALE/CPI as the input variable. Here are the time series plot and ACF and PACF plots of the original series, which are obtained in the Forecasting procedure by plotting the "residuals" of an ARIMA(0,0,0)x(0,0,0) model with constant:

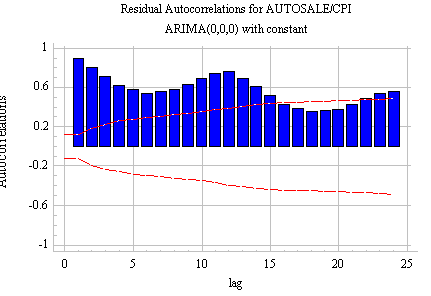
The "suspension bridge" pattern in the ACF is typical of a series that is both nonstationary and strongly seasonal. Clearly we need at least one order of differencing. If we take a nonseasonal difference, the corresponding plots are as follows:

The differenced series (the residuals of a random-walk-with-growth model) looks more-or-less stationary, but there is still very strong autocorrelation at the seasonal period (lag 12).

Because the seasonal pattern is strong and stable, we know (from Rule 12) that we will want to use an order of seasonal differencing in the model. Here is what the picture looks like after a seasonal difference (only):

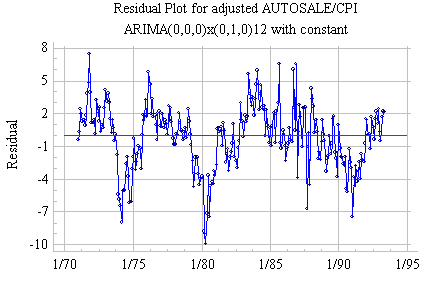
The seasonally differenced series shows a very strong pattern of positive autocorrelation, as we recall from our earlier attempt to fit a seasonal random walk model. This could be an "AR signature"--or it could signal the need for another difference.

If we take both a seasonal and nonseasonal difference, following results are obtained:

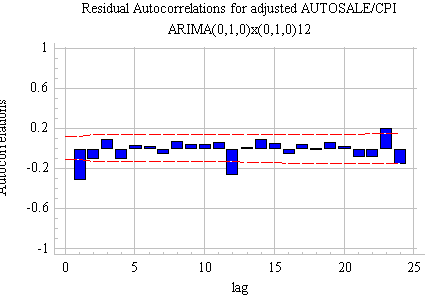
These are, of course, the residuals from the seasonal random trend model that we fitted to the auto sales data earlier. We now see the telltale signs of mild overdifferencing: the positive spikes in the ACF and PACF have become negative.

What is the correct order of differencing? One more piece of information that might be helpful is a calculation of the variance of the series at each level of differencing. This is just the MSE that results from fitting the various difference-only ARIMA models:

Model Comparison

----------------

Data variable: AUTOSALE/CPI

Number of observations = 281

Start index = 1/70            

Sampling interval = 1.0 month(s)

Length of seasonality = 12

Number of periods withheld for validation: 48



Models

------

(A) ARIMA(0,0,0) with constant

(B) ARIMA(0,1,0) with constant

(C) ARIMA(0,0,0)x(0,1,0)12 with constant

(D) ARIMA(0,1,0)x(0,1,0)12 with constant



Estimation Period

Model  MSE          MAE          MAPE         ME           MPE

------------------------------------------------------------------------

(A)    26.2264      4.16826      17.1422      -0.00725956  -4.18066     

(B)    5.67387      1.79003      7.13332      0.007303     -0.413321    

(C)    9.02848      2.30545      9.54065      0.0144368    -0.752748    

(D)    4.9044       1.59         6.25023      -0.00265268  -0.120404

We see that the lowest MSE is obtained by model D which uses one difference of each type. This, together with the appearance of the plots above, strongly suggests that we should use both a seasonal and a nonseasonal difference. Note that, except for the gratuitious constant term, model D is the seasonal random trend (SRT) model, whereas model B is just the seasonal random walk (SRW) model. As we noted earlier when comparing these models, the SRT model appears to fit better than the SRW model. In the analysis that follows, we will try to improve these models through the addition of seasonal ARIMA terms.

The oft-used ARIMA(0,1,1)x(0,1,1) model: SRT model plus MA(1) and SMA(1) terms

Returning to the last set of plots above, notice that with one difference of each type there is a negative spike in the ACF at lag 1 and also a negative spike in the ACF at lag 12, whereas the PACF shows a more gradual "decay" pattern in the vicinity of both these lags. By applying our rules for identifying ARIMA models (specifically, Rule 7 and Rule 13), we may now conclude that the SRT model would be improved by the addition of an MA(1) term and also an SMA(1) term. Also, by Rule 5, we exclude the constant since two orders of differencing are involved. If we do all this, we obtain the often-used ARIMA(0,1,1)x(0,1,1) model, whose residual plots are as follows:

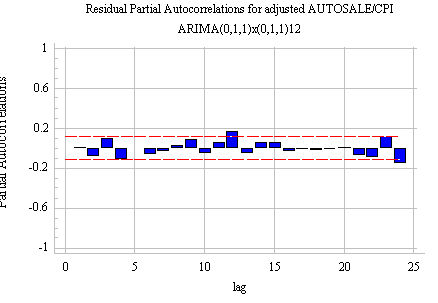
Although a slight amount of autocorrelation remains at lag 12, the overall appearance of the plots is good. The model fitting results show that the estimated MA(1) and SMA(1) coefficients (obtained after 7 iterations) are indeed significant:

Analysis Summary

Data variable: AUTOSALE/CPI

Number of observations = 281

Start index = 1/70            

Sampling interval = 1.0 month(s)

Length of seasonality = 12



Forecast Summary

----------------

Nonseasonal differencing of order: 1

Seasonal differencing of order: 1



Forecast model selected: ARIMA(0,1,1)x(0,1,1)12

Number of forecasts generated: 24

Number of periods withheld for validation: 48



            Estimation      Validation

Statistic   Period          Period

--------------------------------------------

MSE         2.77303         1.83711         

MAE         1.23574         1.05651         

MAPE        4.89559         3.47061         

ME          0.00985809      -0.135525       

MPE         -0.246026       -0.614371       



                            ARIMA Model Summary

Parameter           Estimate        Stnd. Error     t               P-value

----------------------------------------------------------------------------

MA(1)               0.479676        0.0591557       8.1087          0.000000

SMA(1)              0.906532        0.0267735       33.8593         0.000000

----------------------------------------------------------------------------

Backforecasting: yes

Estimated white noise variance = 2.85055 with 266 degrees of freedom

Estimated white noise standard deviation = 1.68836

Number of iterations: 7

The ARIMA(0,1,1)x(0,1,1) model is basically a Seasonal Random Trend (SRT) model fine-tuned by the addition of MA(1) and SMA(1) terms to correct for the mild overdifferencing that resulted from taking two total orders of differencing. THIS IS PROBABLY THE MOST COMMONLY USED SEASONAL ARIMA MODEL. The forecasts from the model resemble those of the seasonal random trend model--i.e., they pick up the seasonal pattern and the local trend at the end of the series--but they are slightly smoother in appearance since both the seasonal pattern and the trend are effectively being averaged (in a exponential-smoothing kind of way) over the last few seasons:

Indeed, the value of the SMA(1) coefficient near 1.0 suggests that many seasons of data are being averaged over to estimate the seasonal pattern. (Recall that an MA(1) coefficient corresponds to "1 minus alpha" in an exponential smoothing model, and that a large MA(1) coefficient therefore corresponds to a small alpha--i.e., a large average age of the data in the smoothed forecast. The SMA(1) coefficient similarly corresponds to "1 minus" a seasonal smoothing coefficient--and a large value of the SMA(1) coefficient suggests a large average age measured in units of seasons of data.) The smaller value of the MA(1) coefficient suggests that relatively little smoothing is being done to estimate the local level and trend--i.e., only the last few months of data are being used for that purpose.

The forecasting equation for this model is:

where little-theta is the MA(1) coefficient and big-theta is the SMA(1) coefficient. Notice that this is just the seasonal random trend model fancied-up by adding multiples of the errors at lags 1, 12, and 13. Also, notice that the coefficient of the lag-13 error is the product of the MA(1) and SMA(1) coefficients.

The ARIMA(1,0,0)x(0,1,0) with constant: SRW model plus AR(1) term

The previous model was a Seasonal Random Trend (SRT) model fine-tuned by the addition of MA(1) and SMA(1) coefficients. An alternative ARIMA model for this series can be obtained by substituting an AR(1) term for the nonseasonal difference--i.e., by adding an AR(1) term to the Seasonal Random Walk (SRW) model. This will allow us to preserve the seasonal pattern in the model while lowering the total amount of differencing, thereby increasing the stability of the trend projections if desired. (Recall that with one seasonal difference alone, the series did show a strong AR(1) signature.) If we do this, we obtain an ARIMA(1,0,0)x(0,1,0) model with constant, which yields the following results:

Analysis Summary

Data variable: AUTOSALE/CPI

Number of observations = 281

Start index = 1/70            

Sampling interval = 1,0 month(s)

Length of seasonality = 12



Forecast Summary

----------------

Seasonal differencing of order: 1

Forecast model selected: ARIMA(1,0,0)x(0,1,0)12 with constant

Number of forecasts generated: 24

Number of periods withheld for validation: 48



            Estimation      Validation

Statistic   Period          Period

--------------------------------------------

MSE         4,24175         3,04301         

MAE         1,4508          1,44661         

MAPE        5,73812         4,78971         

ME          0,0209967       -0,274249       

MPE         -0,214828       -1,00671        



                            ARIMA Model Summary

Parameter           Estimate        Stnd. Error     t               P-value

----------------------------------------------------------------------------

AR(1)               0,72972         0,046205        15,7931         0,000001

Mean                0,75596         0,508192        1,48755         0,138051

Constant            0,204321        

----------------------------------------------------------------------------

Backforecasting: yes

Estimated white noise variance = 4,24182 with 267 degrees of freedom

Estimated white noise standard deviation = 2,05957

Number of iterations: 1

The AR(1) coefficient is indeed highly significant, and the MSE is only 4.24, compared to the 9.028 for the unadulterated SRW model (Model B in the comparison report above). The forecasting equation for this model is:

The additional term on the right-hand-side is a multiple of the seasonal difference observed in the last month, which has the effect of correcting the forecast for the effect of an unusually "good" or "bad" year. Here "phi" denotes the AR(1) coefficient, whose estimated value is 0.73. Thus, for example, if sales last month were X dollars ahead of sales one year earlier, then the quantity 0.73X would be added to the forecast for this month.

The forecast plot shows that the model indeed does a better job than the SRW model of tracking cyclical changes (i.e., unusually good or bad years):

However, the MSE for this model is still significantly larger than what we obtained for the ARIMA(0,1,1)x(0,1,1) model. If we look at the plots of residuals, we see room for improvement. The residuals still show some sign of cyclical variation:

The ACF and PACF suggest the need for both MA(1) and SMA(1) coefficients:

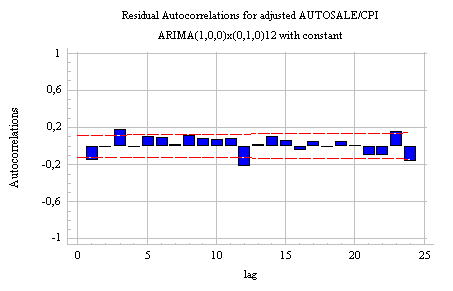
An improved version: ARIMA(1,0,1)x(0,1,1) with constant

If we add the indicated MA(1) and SMA(1) terms to the preceding model, we obtain an ARIMA(1,0,1)x(0,1,1) model with constant. This is nearly the same as the ARIMA(0,1,1)x(0,1,1) model except that it replaces the nonseasonal difference with an AR(1) term (a "partial difference") and it incorporates a constant term representing the long-term trend. Hence, this model assumes a more stable long-term trend than the ARIMA(0,1,1)x(0,1,1) model. The model-fitting results are as follows:

Analysis Summary

Data variable: AUTOSALE/CPI

Number of observations = 281

Start index = 1/70            

Sampling interval = 1.0 month(s)

Length of seasonality = 12



Forecast Summary

----------------

Seasonal differencing of order: 1



Forecast model selected: ARIMA(1,0,1)x(0,1,1)12 with constant

Number of forecasts generated: 24

Number of periods withheld for validation: 48



            Estimation      Validation

Statistic   Period          Period

--------------------------------------------

MSE         2.75399         1.81308         

MAE         1.22287         1.05989         

MAPE        4.84797         3.49931         

ME          0.0297479       -0.262108       

MPE         -0.23536        -1.04485        



                            ARIMA Model Summary

Parameter           Estimate        Stnd. Error     t               P-value

----------------------------------------------------------------------------

AR(1)               0.959688        0.0220179       43.5868         0.000000

MA(1)               0.446023        0.0675235       6.60545         0.000000

SMA(1)              0.905846        0.0272139       33.2861         0.000000

Mean                0.681967        0.259388        2.62914         0.009060

Constant            0.0274918       

----------------------------------------------------------------------------

Backforecasting: yes

Estimated white noise variance = 2.80968 with 265 degrees of freedom

Estimated white noise standard deviation = 1.67621

Number of iterations: 9

Notice that the estimated AR(1) coefficient is very close to 1.0 (in fact, less than two standard errors away from 1.0) and that the other statistics of the model (the estimated MA(1) and SMA(1) coefficients and error statistics in the estimation and validation periods) are otherwise nearly identical to those of the previous model. A constant term has been included in this model because it has only one order of differencing, and the long-term forecasts from the model will therefore reflect the average trend over the whole history of the series rather than the local trend at the end of the series--this is the principal difference between this model and the preceding one. The estimated MEAN of 0.68 is the average annual increase.

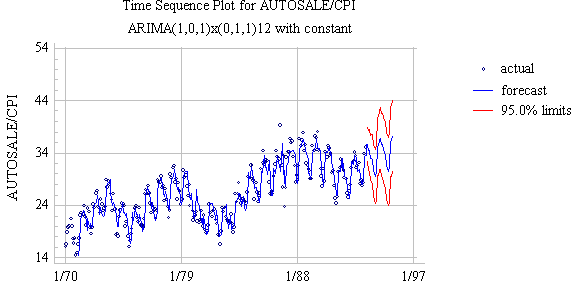
The forecasts from this model look quite similar to those of the preceding model, because the average trend is similar to the local trend at the end of the series. However, the confidence intervals for the model with a lower order of total differencing widen somewhat less rapidly. Notice that the confidence limits for the two-year-ahead forecasts now stay within the horizontal grid lines at 24 and 44:

The forecasting equation for this model is:

This is the same as the equation for the ARIMA(0,1,1)x(0,1,1) model, except that an AR(1) coefficient ("phi") now multiplies the Y(t-1)-Y(t-13) term, and a CONSTANT (mu) has been added. When phi is equal to 1 and mu is equal to zero, it becomes exactly the same as the previous equation--i.e., the AR(1) term becomes equivalent to a nonseasonal difference.

Seasonal ARIMA versus exponential smoothing and seasonal adjustment: Now let's compare the performance the ARIMA models against simple and linear exponential smoothing models accompanied by multiplicative seasonal adjustment:

Model Comparison

----------------

Data variable: AUTOSALE/CPI

Number of observations = 281

Start index = 1/70            

Sampling interval = 1.0 month(s)

Length of seasonality = 12

Number of periods withheld for validation: 48



Models

------

(A) ARIMA(0,1,0)x(0,1,0)12

(B) ARIMA(0,1,1)x(0,1,1)12

(C) ARIMA(1,0,1)x(0,1,1)12 with constant

(D) Simple exponential smoothing with alpha = 0.4772

    Seasonal adjustment: Multiplicative

(E) Brown's linear exp. smoothing with alpha = 0.2106

    Seasonal adjustment: Multiplicative



Estimation Period

Model  MSE          MAE          MAPE         ME           MPE

------------------------------------------------------------------------

(A)    4.8821       1.58984      6.24946      0.00164081   -0.10311     

(B)    2.77303      1.23574      4.89559      0.00985809   -0.246026    

(C)    2.75399      1.22287      4.84797      0.0297479    -0.23536     

(D)    2.639        1.18753      4.76707      0.131989     0.233418     

(E)    2.78296      1.24417      5.03819      0.00321996   -0.146439    



Model  RMSE         RUNS  RUNM  AUTO  MEAN  VAR

-----------------------------------------------

(A)    2.20955       OK    *     ***   OK   ***  

(B)    1.66524       OK    OK    OK    OK   ***  

(C)    1.65951       OK    OK    *     OK   ***  

(D)    1.6245        OK    OK    ***   OK   ***  

(E)    1.66822       OK    OK    ***   OK   ***  



Validation Period

Model  MSE          MAE          MAPE         ME           MPE

------------------------------------------------------------------------

(A)    3.4813       1.45537      4.83928      0.0460732    0.0818369    

(B)    1.83711      1.05651      3.47061      -0.135525    -0.614371    

(C)    1.81308      1.05989      3.49931      -0.262108    -1.04485     

(D)    1.87575      1.07203      3.48819      -0.040363    -0.279181    

(E)    1.908        1.07484      3.48071      0.0778136    0.115798

Here, model A is the seasonal random trend model, models B and C are the two ARIMA models analyzed above, and models D and E are simple and linear exponential smoothing, respectively, with multiplicative seasonal adjustment. It's quite hard to pick among the last four models based on these statistics alone!

What are the tradeoffs among the various seasonal models? The two models that use multiplicative seasonal adjustment deal with seasonality in an explicit fashion--i.e., seasonal indices are broken out as an explicit part of the model. The ARIMA models deal with seasonality in a more implicit manner--we can't easily see in the ARIMA output how the average December, say, differs from the average July. Depending on whether it is deemed important to isolate the seasonal pattern, this might be a factor in choosing among models. The ARIMA models have the advantage that, once they have been initialized, they have fewer "moving parts" than the exponential smoothing and adjustment models. For example, they could be more compactly implemented on a spreadsheet.

Between the two ARIMA models, one (model B) estimates a time-varying trend, while the other (model C) incorporates a long-term average trend. (We could, if we desired, flatten out the long-term trend in model C by suppressing the constant term.) Between the two exponential-smoothing-plus-adjustment models, one (model D) assumes a "flat" trend at all times, while the other (model E) assumes a time-varying trend. Therefore, the assumptions we are most comfortable making about the nature of the long-term trend should be another determining factor in our choice of models. The models that do not assume time-varying trends generally have narrower confidence intervals for longer-horizon forecasts.

To log or not to log? Something that we have not yet done, but might have, is include a log transformation as part of the model. Seasonal ARIMA models are inherently additive models, so if we want to capture a multiplicative seasonal pattern, we must do so by logging the data prior to fitting the ARIMA model. (In Statgraphics, we would just have to specify "Natural Log" as a modeling option--no big deal.) In this case, the deflation transformation seems to have done a satisfactory job of stabilizing the amplitudes of the seasonal cycles, so there does not appear to be a compelling reason to add a log transformation. If the residuals showed a marked increase in variance over time, we might decide otherwise.

Summary of rules for identifying ARIMA models

Identifying the order of differencing and the constant:

Rule 1: If the series has positive autocorrelations out to a high number of lags, then it probably needs a higher order of differencing.
Rule 2: If the lag-1 autocorrelation is zero or negative, or the autocorrelations are all small and patternless, then the series does not need a higher order of differencing. If the lag-1 autocorrelation is -0.5 or more negative, the series may be overdifferenced. BEWARE OF OVERDIFFERENCING!!
Rule 3: The optimal order of differencing is often the order of differencing at which the standard deviation is lowest.
Rule 4: A model with no orders of differencing assumes that the original series is stationary (among other things, mean-reverting). A model with one order of differencing assumes that the original series has a constant average trend (e.g. a random walk or SES-type model, with or without growth). A model with two orders of total differencing assumes that the original series has a time-varying trend (e.g. a random trend or LES-type model).
Rule 5: A model with no orders of differencing normally includes a constant term (which represents the mean of the series). A model with two orders of total differencing normally does not include a constant term. In a model with one order of total differencing, a constant term should be included if the series has a non-zero average trend.

Identifying the numbers of AR and MA terms:

Rule 6: If the partial autocorrelation function (PACF) of the differenced series displays a sharp cutoff and/or the lag-1 autocorrelation is positive--i.e., if the series appears slightly "underdifferenced"--then consider adding one or more AR terms to the model. The lag beyond which the PACF cuts off is the indicated number of AR terms.
Rule 7: If the autocorrelation function (ACF) of the differenced series displays a sharp cutoff and/or the lag-1 autocorrelation is negative--i.e., if the series appears slightly "overdifferenced"--then consider adding an MA term to the model. The lag beyond which the ACF cuts off is the indicated number of MA terms.
Rule 8: It is possible for an AR term and an MA term to cancel each other's effects, so if a mixed AR-MA model seems to fit the data, also try a model with one fewer AR term and one fewer MA term--particularly if the parameter estimates in the original model require more than 10 iterations to converge.
Rule 9: If there is a unit root in the AR part of the model--i.e., if the sum of the AR coefficients is almost exactly 1--you should reduce the number of AR terms by one and increase the order of differencing by one.
Rule 10: If there is a unit root in the MA part of the model--i.e., if the sum of the MA coefficients is almost exactly 1--you should reduce the number of MA terms by one and reduce the order of differencing by one.
Rule 11: If the long-term forecasts appear erratic or unstable, there may be a unit root in the AR or MA coefficients.

Identifying the seasonal part of the model:

Rule 12: If the series has a strong and consistent seasonal pattern, then you should use an order of seasonal differencing--but never use more than one order of seasonal differencing or more than 2 orders of total differencing (seasonal+nonseasonal).
Rule 13: If the autocorrelation at the seasonal period is positive, consider adding an SAR term to the model. If the autocorrelation at the seasonal period is negative, consider adding an SMA term to the model. Do not mix SAR and SMA terms in the same model, and avoid using more than one of either kind.