Simulations and Statistical Inference

In [1]:

library(tidyverse)

── Attaching packages ─────────────────────────────────────── tidyverse 1.2.1 ──
✔ ggplot2 2.2.1     ✔ purrr   0.2.5
✔ tibble  1.4.2     ✔ dplyr   0.7.5
✔ tidyr   0.8.1     ✔ stringr 1.3.1
✔ readr   1.1.1     ✔ forcats 0.3.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()

In [2]:

options(repr.plot.width=4, repr.plot.height=3)

Set random number seed for reproucibility

In [3]:

set.seed(42)

Generating numbers

Using the c function

In [4]:

c(1,2,3,5,8,13)
  1. 1
  2. 2
  3. 3
  4. 5
  5. 8
  6. 13

Using the : operator

In [5]:

1:10
  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
In [6]:

10:1
  1. 10
  2. 9
  3. 8
  4. 7
  5. 6
  6. 5
  7. 4
  8. 3
  9. 2
  10. 1

Using the seq function

In [7]:

seq(1, 10)
  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
In [8]:

seq(1, 10, 2)
  1. 1
  2. 3
  3. 5
  4. 7
  5. 9
In [9]:

seq(10, 1, -1)
  1. 10
  2. 9
  3. 8
  4. 7
  5. 6
  6. 5
  7. 4
  8. 3
  9. 2
  10. 1
In [10]:

seq(0, 1, length.out = 11)
  1. 0
  2. 0.1
  3. 0.2
  4. 0.3
  5. 0.4
  6. 0.5
  7. 0.6
  8. 0.7
  9. 0.8
  10. 0.9
  11. 1

Using rep

rep is useful for generating repeating data patterns.

In [11]:

rep(3, 5)
  1. 3
  2. 3
  3. 3
  4. 3
  5. 3
In [12]:

rep(1:3, times=5)
  1. 1
  2. 2
  3. 3
  4. 1
  5. 2
  6. 3
  7. 1
  8. 2
  9. 3
  10. 1
  11. 2
  12. 3
  13. 1
  14. 2
  15. 3
In [13]:

rep(1:3, each=5)
  1. 1
  2. 1
  3. 1
  4. 1
  5. 1
  6. 2
  7. 2
  8. 2
  9. 2
  10. 2
  11. 3
  12. 3
  13. 3
  14. 3
  15. 3
In [14]:

rep(1:3, length.out=10)
  1. 1
  2. 2
  3. 3
  4. 1
  5. 2
  6. 3
  7. 1
  8. 2
  9. 3
  10. 1

Using sample

Simulate n tooses of a coin

In [15]:

n <- 10

In [16]:

t1 <- sample(c('H', 'T'), n, replace = TRUE)
t1
  1. 'T'
  2. 'T'
  3. 'H'
  4. 'T'
  5. 'T'
  6. 'T'
  7. 'T'
  8. 'H'
  9. 'T'
  10. 'T'
In [17]:

table(t1)

t1
H T
2 8

Simulate n tosses of a biased coin

In [18]:

t2 <- sample(c('H', 'T'), n, replace = TRUE, prob = c(0.3, 0.7))
t2
  1. 'T'
  2. 'H'
  3. 'H'
  4. 'T'
  5. 'T'
  6. 'H'
  7. 'H'
  8. 'T'
  9. 'T'
  10. 'T'
In [19]:

table(t2)

t2
H T
4 6

Simulate n rolls of a 6-sided die

In [20]:

n <- 100

In [21]:

d1 <- sample(1:6, n, replace=TRUE)
d1
  1. 6
  2. 1
  3. 6
  4. 6
  5. 1
  6. 4
  7. 3
  8. 6
  9. 3
  10. 6
  11. 5
  12. 5
  13. 3
  14. 5
  15. 1
  16. 5
  17. 1
  18. 2
  19. 6
  20. 4
  21. 3
  22. 3
  23. 1
  24. 6
  25. 3
  26. 6
  27. 6
  28. 4
  29. 6
  30. 4
  31. 3
  32. 3
  33. 3
  34. 5
  35. 1
  36. 5
  37. 5
  38. 2
  39. 2
  40. 4
  41. 5
  42. 6
  43. 5
  44. 4
  45. 6
  46. 2
  47. 2
  48. 5
  49. 5
  50. 2
  51. 1
  52. 1
  53. 2
  54. 3
  55. 2
  56. 5
  57. 1
  58. 3
  59. 4
  60. 1
  61. 4
  62. 1
  63. 3
  64. 4
  65. 5
  66. 4
  67. 2
  68. 1
  69. 1
  70. 2
  71. 5
  72. 1
  73. 2
  74. 6
  75. 6
  76. 5
  77. 2
  78. 4
  79. 5
  80. 4
  81. 4
  82. 2
  83. 2
  84. 3
  85. 6
  86. 6
  87. 5
  88. 5
  89. 4
  90. 1
  91. 4
  92. 6
  93. 5
  94. 3
  95. 4
  96. 4
  97. 1
  98. 3
  99. 4
  100. 5
In [22]:

table(d1)

d1
 1  2  3  4  5  6
16 14 15 18 20 17

Sampling without replacement. For example, if we wanted to assiggn 16 samples to treatment A or B at random such that exactly half had each treatment.

In [23]:

sample(rep(c('A', 'B'), each=8))
  1. 'A'
  2. 'A'
  3. 'B'
  4. 'A'
  5. 'B'
  6. 'A'
  7. 'B'
  8. 'B'
  9. 'A'
  10. 'B'
  11. 'B'
  12. 'A'
  13. 'A'
  14. 'B'
  15. 'B'
  16. 'A'

Random number generators

Disscrete distributionns

Sampling from a Bernoullli distribution returns TRUE for success and FALSE for failure.

In [24]:

rbernoulli(n=10, p=0.5)
  1. TRUE
  2. FALSE
  3. TRUE
  4. TRUE
  5. FALSE
  6. FALSE
  7. FALSE
  8. TRUE
  9. TRUE
  10. TRUE
In [25]:

as.integer(rbernoulli(n=10, p=0.5))
  1. 0
  2. 1
  3. 0
  4. 0
  5. 1
  6. 0
  7. 1
  8. 0
  9. 1
  10. 1

Sampling from a Binomial distribution returns the number of successes in size trials for n experiments.

In [26]:

rbinom(n=10, p=0.5, size=5)
  1. 2
  2. 0
  3. 1
  4. 3
  5. 4
  6. 3
  7. 3
  8. 2
  9. 3
  10. 1

Sampling from a negative binomial distribution returns the number of failures until size succcesses are observed for n experiemnts.

In [27]:

rnbinom(n=10, size=5, prob=0.5)
  1. 2
  2. 5
  3. 6
  4. 7
  5. 6
  6. 6
  7. 5
  8. 1
  9. 0
  10. 9

Sampling from a Poisson distribution returns the number of successes in n experiments if the average success rate per experiment is lambda.

In [28]:

rpois(n=10, lambda = 3)
  1. 3
  2. 5
  3. 3
  4. 1
  5. 3
  6. 7
  7. 3
  8. 2
  9. 2
  10. 3

Note: We can give different parameters for each experiment in these distributios.

In [54]:

rpois(n=10, lambda=1:10)
  1. 2
  2. 2
  3. 3
  4. 5
  5. 6
  6. 3
  7. 6
  8. 8
  9. 9
  10. 9

Continuous distributions

Sampling from a stnadard uniform distribution.

In [29]:

runif(5)
  1. 0.649875837611035
  2. 0.336419132305309
  3. 0.0609497462864965
  4. 0.451310850214213
  5. 0.838755033444613

Sampling form a uniform distribuiotn,

In [30]:

runif(5, 90, 100)
  1. 95.7463733432814
  2. 93.5335037740879
  3. 95.4742607823573
  4. 98.9271859382279
  5. 94.8999057058245

Sampling from a stnadard normal distribution.

In [31]:

rnorm(5)
  1. -0.94773529068477
  2. 1.76797780755595
  3. 0.917327777548805
  4. -0.894775408854386
  5. -0.688165944958397

Looping

In [90]:

for (i in 1:10) {
    print(mean(rnorm(10)))
}

[1] 0.2660734
[1] -0.09742615
[1] -0.3068994
[1] 0.2910631
[1] 0.1062726
[1] 0.05955272
[1] 0.4080255
[1] -0.1243275
[1] -0.779981
[1] -0.187303

Saving variabels generated in a loop

In [91]:

n <- 10
vars <- numeric(n)
for (i in 1:n) {
    vars[i] <- mean(rnorm(10))
}
vars
  1. -0.25116755575127
  2. 0.708916638976887
  3. 0.461551515258198
  4. -0.475557761331935
  5. -0.0598841272831985
  6. 0.272569234838853
  7. 0.0543736652184016
  8. 0.135002662203851
  9. -0.190719191248592
  10. 0.0387989282162199

Using replicate

replicate is like rep but works for a function (such as a random number geenerator)

In [32]:

replicate(3, rnorm(5))
-0.9984839 0.15461594-0.88368060
-2.1072414 -0.80160087 0.07714041
0.8574190 -0.04518119 0.83720136
1.1260757 -1.03824075 0.09992556
-0.1983684 1.55953311 0.30272834

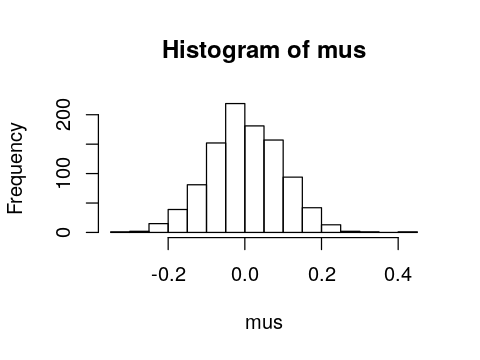
replicate is quite useful for simulations. For exampe, suppose we want to know the distribution of the sample mean if we sampled 100 numbers from the standard normal distribution 1,000 times.

In [ ]:

n_expts <- 1000
n <- 100

Using for loop

In [86]:

set.seed(123)
mus <- numeric(n_expts)
for (i in 1:n_expts) {
    mus[i] <- mean(rnorm(n))
}
hist(mus)
../_images/cliburn_Statistical_Inference_01_64_0.png

Using replicate

In [89]:

set.seed(123)
mus <- replicate(n_expts, mean(rnorm(n)))
hist(mus)
../_images/cliburn_Statistical_Inference_01_66_0.png

Makign a data.frame of simulated data

Let’s simulate the following experiment.

  • There are 10 subjects in Group A and 10 subjects in Group B with ranodm PIDs from 10000-99999
  • We measure 5 genes in each subject. The genes have the same distribution for each subject, but different genes have differnt distribtutions:
    • gene1 \(\sim N(10, 1)\)
    • gene2 \(\sim N(11, 2)\)
    • gene3 \(\sim N(12, 3)\)
    • gene4 \(\sim N(13, 4)\)
    • gene5 \(\sim (N(14, 5)\)
In [48]:

replicate(5, rnorm(3, 1:5, 1))
0.65364261.334889 1.54323020.65734782.249920
1.35856362.068446 0.89367474.22711723.146313
3.40236612.388056 2.63943861.58613982.943069 
In [75]:

n <- 10
n_genes <- 5
min_pid <- 10000
max_pid <- 99999
groupings <- c('A', 'B')
n_groups <- length(groupings)
gene_mus <- 10:14
gene_sigmas <- 1:5
pad_width <- 3

In [76]:

pids <- sample(min_pid:max_pid, n_groups*n)
groups <- sample(rep(groupings, each=n))
genes <- t(replicate(n_groups*n, rnorm(n_genes, gene_mus, gene_sigmas)))
gene_names <- paste('gene', str_pad(1:n_genes, width = pad_width, pad='0'), sep='')
colnames(genes) <- gene_names

In [77]:

df <- data.frame(
    pid = pids,
    grp = groups,
    genes
)

In [58]:

sample_n(df, 3)
pidgrpgene001gene002gene003gene004gene005
1638729 B 1.530708 8.61394310.617613 9.2155139.880912
1322215 B 14.54560910.625483 6.288087 9.7414669.624057
1489658 A 13.00822414.321570 8.11567612.6085647.962775

Breakdown of simjulation

Set up simulation confiugration parameters.

In [70]:

n <- 10
n_genes <- 5
min_pid <- 10000
max_pid <- 99999
groupings <- c('A', 'B')
n_groups <- length(groupings)
gene_mus <- 10:14
gene_sigmas <- 1:5
pad_width <- 3

Create unique PIDs for each subject

In [62]:

pids <- sample(min_pid:max_pid, n_groups*n)

Assign a group to each subject at ranodm

In [67]:

groups <- sample(rep(groupings, each=n))

Make up 5 genes from different distributions for each subject

In [68]:

genes <- t(replicate(n_groups*n, rnorm(n_genes, gene_mus, gene_sigmas)))

Make nice names for each gene

In [71]:

gene_names <- paste('gene', str_pad(1:n_genes, width = pad_width, pad='0'), sep='')

Assign names to gene columns

In [72]:

colnames(genes) <- gene_names

Create data.frame to storre simulated data

In [73]:

df <- data.frame(
    pid = pids,
    grp = groups,
    genes
)

Peek into data.frame

In [74]:

sample_n(df, 3)
pidgrpgene001gene002gene003gene004gene005
1672254 B 10.726324 9.749522 9.77283219.65021 13.226052
1821661 B 10.44887812.68983313.29283219.66553 14.330836
1491408 B 9.12594911.00927313.05214114.95065 8.745456