import os
import sys
import glob
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
%precision 4
np.random.seed(1)
plt.style.use('ggplot')
Computer numbers and mathematics¶
For this course, we will only be concerned with fixed point numbers (representing integers) and floating point numbers (representing reals). Since computer represnetaions of numbers are finite, they are only approximations to the integer ring and real field of mathematics. This notebook presents a small list of things to be mindful of to avoid unexpected results.
References
- https://docs.python.org/2/tutorial/floatingpoint.html
- http://introcs.cs.princeton.edu/java/lectures/9scientific.pdf
The Julia language has a particularly friendly and comprehensive intorduction to computer arithmetic which is also appicable to Python.
Some examples of numbers behaving badly¶
Normalizing weights¶
Given a set of weights, we want to nromalize them so that the sum = 1.
def normalize(ws):
"""Returns normalized set of weights that sum to 1."""
s = sum(ws)
return [w/s for w in ws]
ws = [1,2,3,4,5]
normalize(ws)
[0, 0, 0, 0, 0]
Comparing likleihoods¶
Assuming indepdnece, the likelihood of observing some data points given a distributional model for each data point is the product of the likelihood for each data point.
from scipy.stats import norm
rv1 = norm(0, 1)
rv2 = norm(0, 3)
xs = np.random.normal(0, 3, 1000)
likelihood1 = np.prod(rv1.pdf(xs))
likelihood2 = np.prod(rv2.pdf(xs))
likelihood2 > likelihood1
False
Equality comparisons¶
We use an equality condition to exit some loop.
s = 0.0
for i in range(1000):
s += 1.0/10.0
if s == 1.0:
break
print i
999
Calculating variance¶
def var(xs):
"""Returns variance of sample data."""
n = 0
s = 0
ss = 0
for x in xs:
n +=1
s += x
ss += x*x
v = (ss - (s*s)/n)/(n-1)
return v
# What is the sample variance for numbers from a normal distribution with variance 1?
np.random.seed(4)
xs = np.random.normal(1e9, 1, 1000)
var(xs)
-262.4064
Finite representation of numbers¶
For integers, there is a maximum and minimum representatble number for langauges. Python integers are acutally objects, so they intelligently switch to arbitrary precision numbers when you go beyond these limits, but this is not true for most other languages including C and R. With 64 bit representation, the maximumm is 2^63 - 1 and the minimum is -2^63 - 1.
import sys
sys.maxint
9223372036854775807
2**63-1 == sys.maxint
True
# Python handles "overflow" of integers gracefully by
# swithing from integers to "long" abritrary precsion numbers
sys.maxint + 1
9223372036854775808L
Integer division¶
This has been illustrated more than once, becuase it is such a common source of bugs. Be very careful when dividing one integer by another. Here are some common workarounds.
# Explicit float conversion
print float(1)/3
0.333333333333
# Implicit float conversion
print (0.0 + 1)/3
print (1.0 * 1)/3
0.333333333333
0.333333333333
# Telling Python to ALWAYS do floaitng point with '/'
# Integer division can still be done with '//'
# The __futre__ package contains routines that are only
# found beyond some Python release number.
from __future__ import division
print (1/3)
print (1//3)
0.333333333333
0
Overflow in langauges such as C “wraps around” and gives negative numbers¶
This will not work out of the box because the VM is missing some packages. If you want to really, really want to run this, you can issue the following commands from the command line and have your sudo password ready. It is not necessary to run this - this is just an example to show integer overflow in C - it does not happen in Python.
sudo apt-get update
sudo apt-get install build-essential
sudo apt-get install llvm
pip install git+https://github.com/dabeaz/bitey.git
%%file demo.c
#include "limits.h"
long limit() {
return LONG_MAX;
}
long overflow() {
long x = LONG_MAX;
return x+1;
}
Writing demo.c
! clang -emit-llvm -c demo.c -o demo.o
import bitey
import demo
demo.limit(), demo.overflow()
(9223372036854775807, -9223372036854775808)
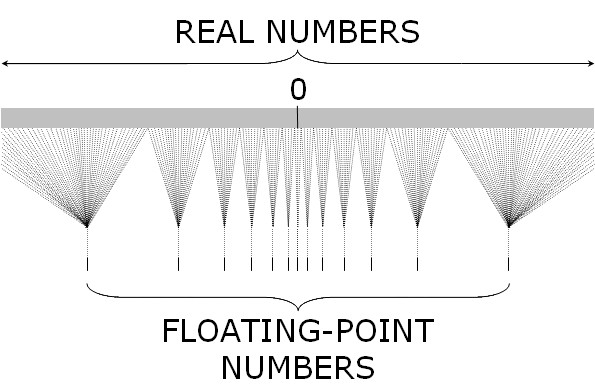
Floating point numbers¶
A floating point number is stored in 3 pieces (sign bit, exponent, mantissa) so that every float is represetned as get +/- mantissa ^ exponent. Because of this, the interval between consecutive numbers is smallest (high precison) for numebrs close to 0 and largest for numbers close to the lower and upper bounds.
Because exponents have to be singed to represent both small and large numbers, but it is more convenint to use unsigned numbers here, the exponnent has an offset (also knwnn as the exponentn bias). For example, if the expoennt is an unsigned 8-bit number, it can rerpesent the range (0, 255). By using an offset of 128, it will now represent the range (-127, 128).
from IPython.display import Image
Binary represetnation of a floating point number¶
Image(url='http://www.dspguide.com/graphics/F_4_2.gif')

Intervals between consecutive floating point numbers are not constant¶
Because of this, if you are adding many numbers, it is more accuate to first add the small numbers before the large numbers.
Image(url='http:///fig1.jpg')
Floating point numbers on your system¶
Information about the floating point reresentation on your system can be
obtained from sys.float_info. Definitions of the stored values are
given at https://docs.python.org/2/library/sys.html#sys.float_info
import sys
print sys.float_info
sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)
Floating point numbers may not be precise¶
'%.20f' % (0.1 * 0.1 * 100)
'1.00000000000000022204'
# Because of this, don't chek for equality of floating point numbers!
# Bad
s = 0.0
for i in range(1000):
s += 1.0/10.0
if s == 1.0:
break
print i
# OK
TOL = 1e-9
s = 0.0
for i in range(1000):
s += 1.0/10.0
if abs(s - 1.0) < TOL:
break
print i
999
9
# Loss of precision
1 + 6.022e23 - 6.022e23
0.0000
Lesson: Avoid algorithms that subtract two numbers that are very close to one anotoer. The loss of significnance is greater when both numbers are very large due to the limited number of precsion bits available.
Associative law does not necessarily hold¶
6.022e23 - 6.022e23 + 1
1.0000
1 + 6.022e23 - 6.022e23
0.0000
Distributive law does not hold¶
a = np.exp(1);
b = np.pi;
c = np.sin(1);
a*(b+c) == a*b+a*c
False
# loss of precision can be a problem when calculating likelihoods
probs = np.random.random(1000)
np.prod(probs)
0.0000
# when multiplying lots of small numbers, work in log space
np.sum(np.log(probs))
-980.0558
Lesson: Work in log space for very small or very big numbers to reduce underflow/overflow
Using arbitrary precision libraries¶
If you need precision more than speed (e.g. your code is likely to underflow or overflow otherwise and you cannot find or don’t want to use a workaround), Python has support for arbitrary precison mathematics via
Both mpmath and gmpy2 can be installed via pip
pip install gmpy2
pip install mpmath
These packages allow you to set the precsion of numbers used in calculations. Refer to the documentation if you need to use these libraries.
From numbers to Functions: Stability and conditioning¶
Suppose we have a computer algorithm \(g(x)\) that represents the mathematical function \(f(x)\). \(g(x)\) is stable if for some small perturbation \(\epsilon\), \(g(x+\epsilon) \approx f(x)\)
A mathematical function \(f(x)\) is well-conditioned if \(f(x + \epsilon) \approx f(x)\) for all small perturbations \(\epsilon\).
That is, the function\(f(x)\) is well-conditioned if the solution varies gradually as problem varies. For a well-conditinoed function, all small perutbations have small effects. However, a poorly-conditioned problem only needs some small perturbations to have large effects. For example, inverting a nearly singluar matrix is a poorly condiitioned problem.
A numerical algorithm \(g(x)\) is numerically-stable if \(g(x) \approx f(x')\) for some \(x' \approx x\). Note that stability is a property that relates the algorithm \(g(x)\) to the problem \(f(x)\).
That is, the algorithm\(g(x)\) is numerically stable if it gives nearly the right answer to nearly the right question. Numerically unstable algorithms tend to amplify approximation errors due to computer arithmetic over time. If we used an infitinte precision numerical system, stable and unstable alorithms would have the same accuracy. However, as we have seen (e.g. variance calculation), when using floating point numbers, algebrically equivaelent algorithms can give different results.
In general, we need both a well-conditinoed problem and nuerical stabilty of the algorihtm to reliably accurate answers. In this case, we can be sure that \(g(x) \approx f(x)\).
Unstable version
# Catastrophic cancellation occurs when subtracitng
# two numbers that are very close to one another
# Here is another example
def f(x):
return (1 - np.cos(x))/(x*x)
x = np.linspace(-4e-8, 4e-8, 100)
plt.plot(x,f(x));
plt.axvline(1.1e-8, color='red')
plt.xlim([-4e-8, 4e-8]);
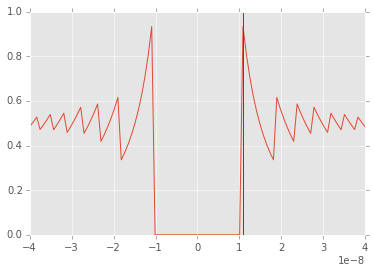
# We know from L'Hopital's rule that the answer is 0.5 at 0
# and should be very close to 0.5 throughout this tiny interval
# but errors arisee due to catastrophic cancellation
print '%.30f' % np.cos(1.1e-8)
print '%.30f' % (1 - np.cos(1.1e-8)) # exact answer is 6.05e-17
print '%2f' % ((1 - np.cos(1.1e-8))/(1.1e-8*1.1e-8))
0.999999999999999888977697537484
0.000000000000000111022302462516
0.917540
Stable version
# Numerically stable version of funtion
# using long-forgotten half-angle formula from trignometry
def f1(x):
return 2*np.sin(x/2)**2/(x*x)
x = np.linspace(-4e-8, 4e-8, 100)
plt.plot(x,f1(x));
plt.axvline(1.1e-8, color='red')
plt.xlim([-4e-8, 4e-8]);
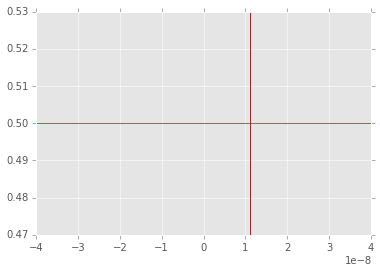
Stable and unstable versions of variance¶
# sum of squares method (vectorized version)
def sum_of_squers_var(x):
n = len(x)
return (1.0/(n*(n-1))*(n*np.sum(x**2) - (np.sum(x))**2))
This should set off warning bells - big number minus big number!
# direct method
def direct_var(x):
n = len(x)
xbar = np.mean(x)
return 1.0/(n-1)*np.sum((x - xbar)**2)
Much better - at least the squaring occurs after the subtraction
# Welford's method
def welford_var(x):
s = 0
m = x[0]
for i in range(1, len(x)):
m += (x[i]-m)/i
s += (x[i]-m)**2
return s/(len(x) -1 )
Classic algorithm from Knuth’s Art of Computer Programming
x_ = np.random.uniform(0,1,1e6)
x = 1e12 + x_
# correct answer
np.var(x_)
0.0835
sum_of_squers_var(x)
737870500.8189
direct_var(x)
0.0835
welford_var(x)
0.0835
Lesson: Mathematical formulas may behave differently when directly translated into code!
This problem also appears in navie algorithms for finding simple regression coefficients and Pearson’s correlation coefficient.
See this series of blog posts for a clear explanation:
- http://www.johndcook.com/blog/2008/09/28/theoretical-explanation-for-numerical-results/
- http://www.johndcook.com/blog/2008/09/26/comparing-three-methods-of-computing-standard-deviation/
- http://www.johndcook.com/blog/2008/10/20/comparing-two-ways-to-fit-a-line-to-data/
- http://www.johndcook.com/blog/2008/11/05/how-to-calculate-pearson-correlation-accurately/
Avoiding catastrophic cancellation by formula rearrangement¶
There are a copule of common tricks that may be useful if you are worried about catastrophic cancellation.
Use library functions where possible¶
Instead of
np.log(x + 1)
which can be inaccurate for \(x\) near zero, use
np.log1p(x)
Similarly, instead of
np.sin(x)/x
use
np.sinc(x)
See if Numpy base functions has what you need.
Rationalize the numerator to remove cancellation for the following problem¶
Use basic algebra to remove canceellation for the following problem¶
Use trignometric identities to remove cancellation for the following 3 problems¶
Poorly conditioned problems¶
# The tangent function is poorly conditioned
x1 = 1.57078
x2 = 1.57079
t1 = np.tan(x1)
t2 = np.tan(x2)
print 't1 =', t1
print 't2 =', t2
print '% change in x =', 100.0*(x2-x1)/x1
print '% change in tan(x) =', (100.0*(t2-t1)/t1)
t1 = 61249.0085315
t2 = 158057.913416
% change in x = 0.000636626389427
% change in tan(x) = 158.057913435
Ill-conditioned matrices
In this example, we want to solve a simple linear system Ax = b where A and b are given.
A = 0.5*np.array([[1,1], [1+1e-10, 1-1e-10]])
b1 = np.array([2,2])
b2 = np.array([2.01, 2])
np.linalg.solve(A, b1)
array([ 2., 2.])
np.linalg.solve(A, b2)
array([-99999989.706, 99999993.726])
The condition number of a matrix is a useful diagnostic - it is defined as the norm of A times the norm of the inverse of A. If this number is large, the matrix is ill-conditioned. Since there are many ways to calculuate a matrix norm, there are also many condition numbers, but they are roughly equivalent for our purpsoes.
np.linalg.cond(A)
19999973849.2252
np.linalg.cond(A, 'fro')
19999998343.1927
Simple things to try with ill-conditioned matrices¶
- Can you remove dependent or collinear variables? If one variable is (almost) an exact muliple of another, it provides no additional information and can be removed from the matrix.
- Can you normalize the data so that all vairables are on the same scale? For example, if columns represent featrue values, standardizign featurres to have zero mean and unit standard deviaiton can be helpful.
- Can you use functions from linear algebra libraries instead of
rolling your own. For example, the
lstsqfunction fromscipy.linalgwill deal with collinear variables sensibly.
Exercises¶
The topic is rather specialized and the main goal is just to have you aware of the “leaky abstraction” of computer numbers as simulations of mathematical numbers, and common situations where this can casue problems. Once you are aware of these areas, you can either avoid them using simple rules, or look for an apprpriate numerical library fuctionn to use instead. So there will be no exericses on the topic of computer arithmetic, conditioning and stability given.
Instead, you need to get as comforatble with the use of arrays in numpy as much as possible for the rest of the course. For practice, see the entertaining examples and exercises at
Nicolas P. Rougier’s numpy tutorial
At the end, there are further links to yet more numpy tutorials!