%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy as scipy
Optimization and Non-linear Methods¶
It is sometimes necessary to solve equations or systems of equations that are non-linear. Often, those non-linear equations arise as optimization problems.
Example: Maximum Likelihood Estimation (MLE)¶
Recall that in MLE, we are interested in estimating the value of a parameter \(\theta\) that maximizes a log-likelihood function \(\ell(X;\theta)\). Let \(X_1,...,X_n\) be an iid set of random variables with pdf \(f(x;\theta)\), where \(\theta \in \mathbb{R}^k\) is a parameter. The likelihood function is:
We want the value of \(\theta\) that maximizes \(L\). We can accomplish this by taking the first derivative (or gradient) of \(L\) with respect to \(\theta\), setting it to zero and solving for \(\theta\). However, this is more easily accomplished if we first take \(\log(L)\), as \(L\) is a product of densities, and taking the log of a product yields a sum. Because \(log\) is a monotonically increasing function, any value of \(\theta\) that maximizes \(\log(L)\) also maximizes \(L\).
Optimization then amounts to finding the zeros of
Bisection Method¶
The bisection method is one of the simplest methods for finding zeroes of a non-linear function. It is guaranteed to find a root - but it can be slow. The main idea comes from the intermediate value theorem: If \(f(a)\) and \(f(b)\) have different signs and \(f\) is continous, then \(f\) must have a zero between \(a\) and \(b\). We evaluate the function at the midpoint, \(c = \frac12(a+b)\). \(f(c)\) is either zero, has the same sign as \(f(a)\) or the same sign as \(f(b)\). Suppose \(f(c)\) has the same sign as \(f(a)\) (as pictured below). We then repeat the process on the interval \([c,b]\).
def f(x):
return x**3 + 4*x**2 -3
x = np.linspace(-3.1, 0, 100)
plt.plot(x, x**3 + 4*x**2 -3)
a = -3.0
b = -0.5
c = 0.5*(a+b)
plt.text(a,-1,"a")
plt.text(b,-1,"b")
plt.text(c,-1,"c")
plt.scatter([a,b,c], [f(a), f(b),f(c)], s=50, facecolors='none')
plt.scatter([a,b,c], [0,0,0], s=50, c='red')
xaxis = plt.axhline(0);

x = np.linspace(-3.1, 0, 100)
plt.plot(x, x**3 + 4*x**2 -3)
d = 0.5*(b+c)
plt.text(d,-1,"d")
plt.text(b,-1,"b")
plt.text(c,-1,"c")
plt.scatter([d,b,c], [f(d), f(b),f(c)], s=50, facecolors='none')
plt.scatter([d,b,c], [0,0,0], s=50, c='red')
xaxis = plt.axhline(0);
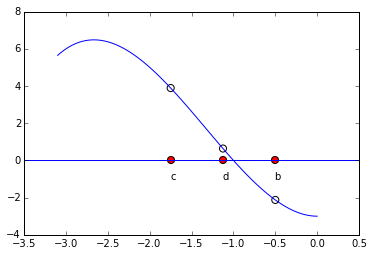
We can terminate the process whenever the function evaluated at the new midpoint is ‘close enough’ to zero.
Secant Method¶
The secant method also begins with two initial points, but without the constraint that the function values are of opposite signs. We use the secant line to extrapolate the next candidate point.
def f(x):
return (x**3-2*x+7)/(x**4+2)
x = np.arange(-3,5, 0.1);
y = f(x)
p1=plt.plot(x, y)
plt.xlim(-3, 4)
plt.ylim(-.5, 4)
plt.xlabel('x')
plt.axhline(0)
t = np.arange(-10, 5., 0.1)
x0=-1.2
x1=-0.5
xvals = []
xvals.append(x0)
xvals.append(x1)
notconverge = 1
count = 0
cols=['r--','b--','g--','y--']
while (notconverge==1 and count < 3):
slope=(f(xvals[count+1])-f(xvals[count]))/(xvals[count+1]-xvals[count])
intercept=-slope*xvals[count+1]+f(xvals[count+1])
plt.plot(t, slope*t + intercept, cols[count])
nextval = -intercept/slope
if abs(f(nextval)) < 0.001:
notconverge=0
else:
xvals.append(nextval)
count = count+1
plt.show()

The secant method has the advantage of fast convergence. While the bisection method has a linear convergence rate (i.e. error goes to zero at the rate that \(h(x) = x\) goes to zero, the secant method has a convergence rate that is faster than linear, but not quite quadratic (i.e. \(\sim x^\alpha\), where \(\alpha = \frac{1+\sqrt{5}}2 \approx 1.6\))
Newton-Rhapson Method¶
We want to find the value \(\theta\) so that some (differentiable) function \(g(\theta)=0\). Idea: start with a guess, \(\theta_0\). Let \(\tilde{\theta}\) denote the value of \(\theta\) for which \(g(\theta) = 0\) and define \(h = \tilde{\theta} - \theta_0\). Then:
This implies that
So that
Thus, we set our next approximation:
and we have developed an interative procedure with:
Example:¶
Let
The graph of this function is:
x = np.arange(-5,5, 0.1);
y = (x**3-2*x+7)/(x**4+2)
p1=plt.plot(x, y)
plt.xlim(-4, 4)
plt.ylim(-.5, 4)
plt.xlabel('x')
plt.axhline(0)
plt.title('Example Function')
plt.show()

x = np.arange(-5,5, 0.1);
y = (x**3-2*x+7)/(x**4+2)
p1=plt.plot(x, y)
plt.xlim(-4, 4)
plt.ylim(-.5, 4)
plt.xlabel('x')
plt.axhline(0)
plt.title('Good Guess')
t = np.arange(-5, 5., 0.1)
x0=-1.5
xvals = []
xvals.append(x0)
notconverge = 1
count = 0
cols=['r--','b--','g--','y--','c--','m--','k--','w--']
while (notconverge==1 and count < 6):
funval=(xvals[count]**3-2*xvals[count]+7)/(xvals[count]**4+2)
slope=-((4*xvals[count]**3 *(7 - 2 *xvals[count] + xvals[count]**3))/(2 + xvals[count]**4)**2) + (-2 + 3 *xvals[count]**2)/(2 + xvals[count]**4)
intercept=-slope*xvals[count]+(xvals[count]**3-2*xvals[count]+7)/(xvals[count]**4+2)
plt.plot(t, slope*t + intercept, cols[count])
nextval = -intercept/slope
if abs(funval) < 0.01:
notconverge=0
else:
xvals.append(nextval)
count = count+1
plt.show()
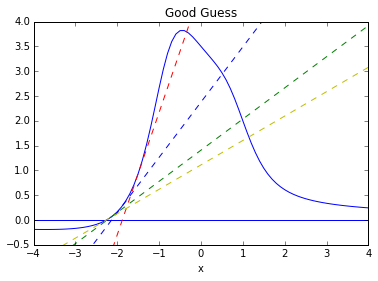
From the graph, we see the zero is near -2. We make an initial guess of
We have made an excellent choice for our first guess, and we can see rapid convergence!
funval
0.007591996330867034
In fact, the Newton-Rhapson method converges quadratically. However, NR (and the secant method) have a fatal flaw:
x = np.arange(-5,5, 0.1);
y = (x**3-2*x+7)/(x**4+2)
p1=plt.plot(x, y)
plt.xlim(-4, 4)
plt.ylim(-.5, 4)
plt.xlabel('x')
plt.axhline(0)
plt.title('Bad Guess')
t = np.arange(-5, 5., 0.1)
x0=-0.5
xvals = []
xvals.append(x0)
notconverge = 1
count = 0
cols=['r--','b--','g--','y--','c--','m--','k--','w--']
while (notconverge==1 and count < 6):
funval=(xvals[count]**3-2*xvals[count]+7)/(xvals[count]**4+2)
slope=-((4*xvals[count]**3 *(7 - 2 *xvals[count] + xvals[count]**3))/(2 + xvals[count]**4)**2) + (-2 + 3 *xvals[count]**2)/(2 + xvals[count]**4)
intercept=-slope*xvals[count]+(xvals[count]**3-2*xvals[count]+7)/(xvals[count]**4+2)
plt.plot(t, slope*t + intercept, cols[count])
nextval = -intercept/slope
if abs(funval) < 0.01:
notconverge = 0
else:
xvals.append(nextval)
count = count+1
plt.show()

We have stumbled on the horizontal asymptote. The algorithm fails to converge.
Basins of Attraction Can Be ‘Close’¶
def f(x):
return x**3 - 2*x**2 - 11*x +12
def s(x):
return 3*x**2 - 4*x - 11
x = np.arange(-5,5, 0.1);
p1=plt.plot(x, f(x))
plt.xlim(-4, 5)
plt.ylim(-20, 22)
plt.xlabel('x')
plt.axhline(0)
plt.title('Basin of Attraction')
t = np.arange(-5, 5., 0.1)
x0=2.43
xvals = []
xvals.append(x0)
notconverge = 1
count = 0
cols=['r--','b--','g--','y--','c--','m--','k--','w--']
while (notconverge==1 and count < 6):
funval = f(xvals[count])
slope = s(xvals[count])
intercept=-slope*xvals[count]+funval
plt.plot(t, slope*t + intercept, cols[count])
nextval = -intercept/slope
if abs(funval) < 0.01:
notconverge = 0
else:
xvals.append(nextval)
count = count+1
plt.show()
xvals[count-1]

-3.1713324128480282
p1=plt.plot(x, f(x))
plt.xlim(-4, 5)
plt.ylim(-20, 22)
plt.xlabel('x')
plt.axhline(0)
plt.title('Basin of Attraction')
t = np.arange(-5, 5., 0.1)
x0=2.349
xvals = []
xvals.append(x0)
notconverge = 1
count = 0
cols=['r--','b--','g--','y--','c--','m--','k--','w--']
while (notconverge==1 and count < 6):
funval = f(xvals[count])
slope = s(xvals[count])
intercept=-slope*xvals[count]+funval
plt.plot(t, slope*t + intercept, cols[count])
nextval = -intercept/slope
if abs(funval) < 0.01:
notconverge = 0
else:
xvals.append(nextval)
count = count+1
plt.show()
xvals[count-1]

0.9991912395651094
Convergence Rate¶
The following is a derivation of the convergence rate of the NR method:
Suppose \(x_k \; \rightarrow \; x^*\) and \(g'(x^*) \neq 0\). Then we may write:
.
Now expand \(g\) at \(x^*\):
We have that
Gauss-Newton¶
For 1D, the Newton method is
We can generalize to \(k\) dimensions by
where \(x\) and \(f(x)\) are now vectors, and \(J^{-1}\) is the inverse Jacobian matrix. In general, the Jacobian is not a square matrix, and we use the generalized inverse \((J^TJ)^{-1}J^T\) instead, giving
In multivariate nonlinear estimation problems, we can find the vector of parameters \(\beta\) by minimizing the residuals \(r(\beta)\),
where the entries of the Jacobian matrix \(J\) are
Inverse Quadratic Interpolation¶
Inverse quadratic interpolation is a type of polynomial interpolation. Polynomial interpolation simply means we find the polynomial of least degree that fits a set of points. In quadratic interpolation, we use three points, and find the quadratic polynomial that passes through those three points.
Inverse quadratic interpolation means we do quadratic interpolation on the inverse function. So, if we are looking for a root of \(f\), we approximate \(f^{-1}(x)\) using quadratic interpolation. Note that the secant method can be viewed as a linear interpolation on the inverse of \(f\). We can write:
We use the above formula to find the next guess \(x_{n+1}\) for a zero of \(f\) (so \(y=0\)):
Convergence rate is approximately \(1.8\).
Brent’s Method¶
Brent’s method is a combination of bisection, secant and inverse quadratic interpolation. Like bisection, it is a ‘bracketed’ method (starts with points \((a,b)\) such that \(f(a)f(b)<0\).
Roughly speaking, the method begins by using the secant method to obtain a third point \(c\), then uses inverse quadratic interpolation to generate the next possible root. Without going into too much detail, the algorithm attempts to assess when interpolation will go awry, and if so, performs a bisection step. Also, it has certain criteria to reject an iterate. If that happens, the next step will be linear interpolation (secant method).
The Brent method is the default method that scypy uses to minimize a univariate function:
from scipy.optimize import minimize_scalar
def f(x):
return (x - 2) * x * (x + 2)**2
res = minimize_scalar(f)
res.x
1.2807764040333458
x = np.arange(-5,5, 0.1);
p1=plt.plot(x, f(x))
plt.xlim(-4, 4)
plt.ylim(-10, 20)
plt.xlabel('x')
plt.axhline(0)
<matplotlib.lines.Line2D at 0x7f9c9b232bd0>
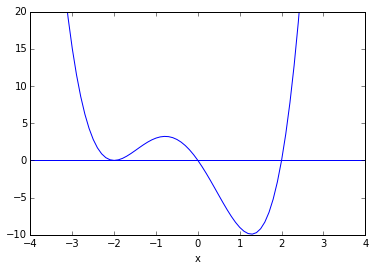
To find zeroes, use
scipy.optimize.brentq(f,-1,.5)
-7.864845203343107e-19
scipy.optimize.brentq(f,.5,3)
2.0
scipy.optimize.newton(f,-3)
-2.0000000172499592