Wrapping R libraries with Rpy¶

from __future__ import division
import os
import sys
import glob
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
%precision 4
plt.style.use('ggplot')

from IPython.core.display import Image
import uuid

import rpy2.robjects as robjects

from rpy2.robjects.packages import importr

fastclime = importr('fastclime')
grdevices = importr('grDevices')

def fastclime_plot(data):
    fn = '{uuid}.png'.format(uuid = uuid.uuid4())
    grdevices.png(fn, width = 800, height = 600)
    fastclime.fastclime_plot(data)
    grdevices.dev_off()
    return Image(filename=fn)

L = fastclime.fastclime_generator(n = 100, d = 20)

out1 = fastclime.fastclime(L.rx2('data'),0.1)
O = fastclime.fastclime_lambda(out1.rx2('lambdamtx'), out1.rx2('icovlist'),0.2)
fastclime_plot(O.rx2('path'))

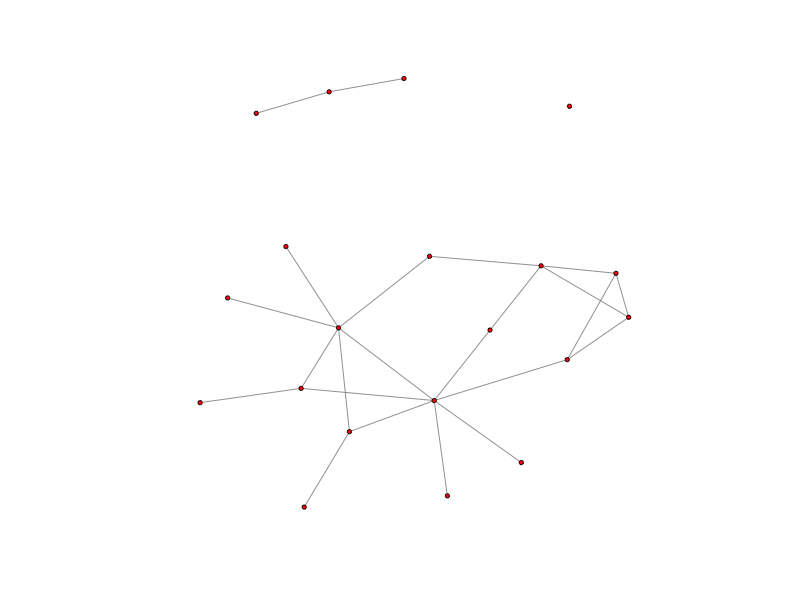
out1 = fastclime.fastclime(cor(L.rx2('data')),0.1)
O = fastclime.fastclime_lambda(out1.rx2('lambdamtx'), out1.rx2('icovlist'),0.2)
fastclime_plot(O.rx2('path'))

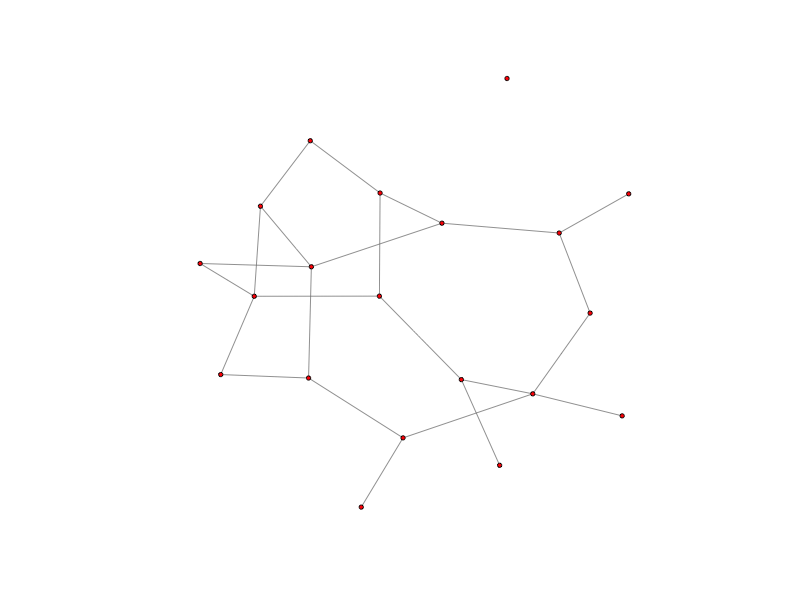
#generate an LP problem and solve it
r_matrix = robjects.r['matrix']

A = r_matrix(robjects.FloatVector([-1,-1,0,1,-2,1]), nrow = 3)
b = robjects.FloatVector([-1,-2,1])
c = robjects.FloatVector ([-2,3])
v = fastclime.fastlp(c,A,b)

v

np.array(v)

#generate an LP problem and solve it

b_bar = robjects.FloatVector([1,1,1])
c_bar = robjects.FloatVector([1,1])
fastclime.paralp(c,A,b,c_bar,b_bar)