from __future__ import division
import os
import sys
import glob
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
%precision 4
plt.style.use('ggplot')
np.random.seed(1234)
import pystan
import scipy.stats as stats
import warnings
warnings.simplefilter('ignore')
PyStan¶
Install PyStan with
pip install pystan
The nice thing about PyMC is that everything is in Python. With
PyStan, however, you need to use a domain specific language based on
C++ syntax to specify the model and the data, which is less flexible and
more work. However, in exchange you get an extremely powerful HMC
package (only does HMC) that can be used in R and Python.
Useful links¶
Coin toss¶
We’ll repeat the example of determining the bias of a coin from observed coin tosses. The likelihood is binomial, and we use a beta prior.
coin_code = """
data {
int<lower=0> n; // number of tosses
int<lower=0> y; // number of heads
}
transformed data {}
parameters {
real<lower=0, upper=1> p;
}
transformed parameters {}
model {
p ~ beta(2, 2);
y ~ binomial(n, p);
}
generated quantities {}
"""
coin_dat = {
'n': 100,
'y': 61,
}
Fit model¶
sm = pystan.StanModel(model_code=coin_code)
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_7f1947cd2d39ae427cd7b6bb6e6ffd77 NOW.
MAP¶
op = sm.optimizing(data=coin_dat)
op
OrderedDict([('p', array(0.6078431219203108))])
MCMC¶
fit = sm.sampling(data=coin_dat)
Loading from a file¶
The string in coin_code can also be in a file - say coin_code.stan
- then we can use it like so
fit = pystan.stan(file='coin_code.stan', data=coin_dat, iter=1000, chains=1)
print(fit)
Inference for Stan model: anon_model_7f1947cd2d39ae427cd7b6bb6e6ffd77.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
p 0.61 7.5e-4 0.05 0.51 0.57 0.61 0.64 0.7 4000 1.0
lp__ -70.24 0.01 0.71 -72.26 -70.39 -69.96 -69.79 -69.74 4000 1.0
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:41:38 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
coin_dict = fit.extract()
coin_dict.keys()
# lp_ is the log posterior
odict_keys(['p', 'lp__'])
We can convert to a DataFrame if necessary¶
df = pd.DataFrame(coin_dict)
df.head(3)
| p | lp__ | |
|---|---|---|
| 0 | 0.634851 | -69.930430 |
| 1 | 0.706164 | -72.132244 |
| 2 | 0.536575 | -70.754119 |
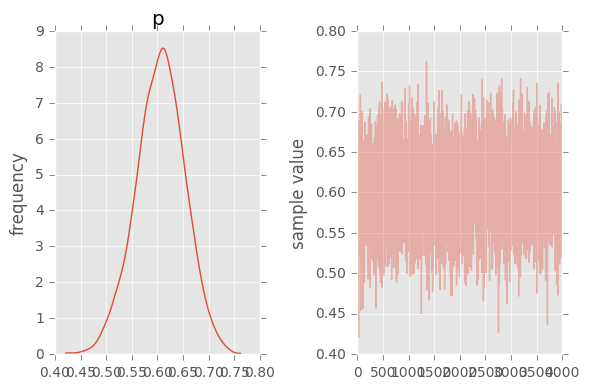
fit.plot('p');
plt.tight_layout()
Estimating mean and standard deviation of normal distribution¶
norm_code = """
data {
int<lower=0> n;
real y[n];
}
transformed data {}
parameters {
real<lower=0, upper=100> mu;
real<lower=0, upper=10> sigma;
}
transformed parameters {}
model {
y ~ normal(mu, sigma);
}
generated quantities {}
"""
norm_dat = {
'n': 100,
'y': np.random.normal(10, 2, 100),
}
fit = pystan.stan(model_code=norm_code, data=norm_dat, iter=1000, chains=1)
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_3318343d5265d1b4ebc1e443f0228954 NOW.
fit
Inference for Stan model: anon_model_3318343d5265d1b4ebc1e443f0228954.
1 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 10.07 9.0e-3 0.2 9.69 9.93 10.07 10.19 10.44 500 1.0
sigma 2.01 5.8e-3 0.13 1.77 1.91 2.0 2.09 2.25 500 1.0
lp__ -117.1 0.04 0.87 -119.5 -117.5 -116.8 -116.4 -116.2 500 1.0
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:42:03 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
trace = fit.extract()
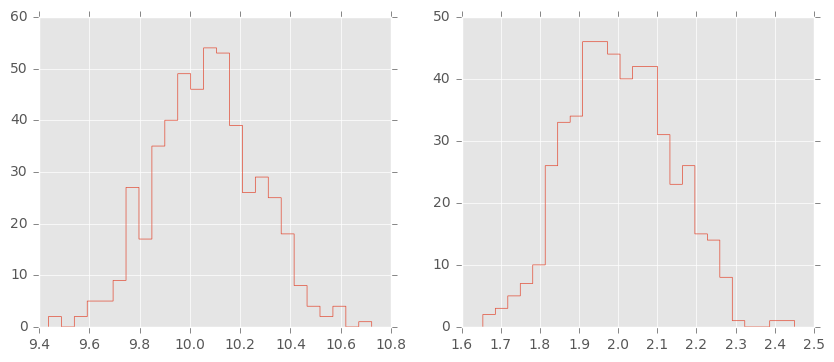
plt.figure(figsize=(10,4))
plt.subplot(1,2,1);
plt.hist(trace['mu'][:], 25, histtype='step');
plt.subplot(1,2,2);
plt.hist(trace['sigma'][:], 25, histtype='step');
Optimization (finding MAP)¶
sm = pystan.StanModel(model_code=norm_code)
op = sm.optimizing(data=norm_dat)
op
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_3318343d5265d1b4ebc1e443f0228954 NOW.
OrderedDict([('mu', array(10.070224531526673)),
('sigma', array(1.9913776026951058))])
Reusing fitted objects¶
new_dat = {
'n': 100,
'y': np.random.normal(10, 2, 100),
}
fit2 = pystan.stan(fit=fit, data=new_dat, chains=1)
fit2
Inference for Stan model: anon_model_3318343d5265d1b4ebc1e443f0228954.
1 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=1000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 9.9 6.3e-3 0.2 9.52 9.77 9.89 10.03 10.32 1000 1.0
sigma 1.99 4.5e-3 0.14 1.73 1.89 1.98 2.08 2.3 1000 1.0
lp__ -115.5 0.03 0.99 -118.1 -115.9 -115.1 -114.7 -114.5 1000 1.0
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:42:29 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
Saving compiled models¶
We can also compile Stan models and save them to file, so as to reload them for later use without needing to recompile.
def save(obj, filename):
"""Save compiled models for reuse."""
import pickle
with open(filename, 'wb') as f:
pickle.dump(obj, f, protocol=pickle.HIGHEST_PROTOCOL)
def load(filename):
"""Reload compiled models for reuse."""
import pickle
return pickle.load(open(filename, 'rb'))
model = pystan.StanModel(model_code=norm_code)
save(model, 'norm_model.pic')
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_3318343d5265d1b4ebc1e443f0228954 NOW.
new_model = load('norm_model.pic')
fit4 = new_model.sampling(new_dat, chains=1)
fit4
Inference for Stan model: anon_model_3318343d5265d1b4ebc1e443f0228954.
1 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=1000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 9.92 6.7e-3 0.21 9.49 9.77 9.91 10.07 10.32 1000 1.01
sigma 1.99 4.3e-3 0.14 1.75 1.89 1.98 2.07 2.29 1000 1.0
lp__ -115.5 0.03 1.0 -118.2 -115.9 -115.2 -114.8 -114.5 1000 1.0
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:42:54 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
Estimating parameters of a linear regression model¶
We will show how to estimate regression parameters using a simple linear model
We can restate the linear model
as sampling from a probability distribution
We will assume the following priors
lin_reg_code = """
data {
int<lower=0> n;
real x[n];
real y[n];
}
transformed data {}
parameters {
real a;
real b;
real sigma;
}
transformed parameters {
real mu[n];
for (i in 1:n) {
mu[i] <- a*x[i] + b;
}
}
model {
sigma ~ uniform(0, 20);
y ~ normal(mu, sigma);
}
generated quantities {}
"""
n = 11
_a = 6
_b = 2
x = np.linspace(0, 1, n)
y = _a*x + _b + np.random.randn(n)
lin_reg_dat = {
'n': n,
'x': x,
'y': y
}
fit = pystan.stan(model_code=lin_reg_code, data=lin_reg_dat, iter=1000, chains=1)
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_4bdbb0aeaf5fafee91f7aa8b257093f2 NOW.
fit
Inference for Stan model: anon_model_4bdbb0aeaf5fafee91f7aa8b257093f2.
1 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a 7.27 0.04 0.97 5.48 6.64 7.24 7.83 9.24 500 1.02
b 1.51 0.03 0.56 0.25 1.21 1.55 1.85 2.62 500 1.01
sigma 0.94 0.01 0.3 0.54 0.75 0.87 1.05 1.69 500 1.0
mu[0] 1.51 0.03 0.56 0.25 1.21 1.55 1.85 2.62 500 1.01
mu[1] 2.24 0.02 0.48 1.15 1.99 2.26 2.51 3.25 500 1.01
mu[2] 2.97 0.02 0.41 2.06 2.75 2.98 3.2 3.8 500 1.01
mu[3] 3.7 0.02 0.35 2.96 3.5 3.71 3.89 4.38 500 1.0
mu[4] 4.42 0.01 0.31 3.79 4.24 4.43 4.58 5.01 500 1.0
mu[5] 5.15 0.01 0.3 4.57 4.97 5.17 5.31 5.72 500 1.0
mu[6] 5.88 0.01 0.31 5.23 5.7 5.88 6.05 6.51 500 1.0
mu[7] 6.6 0.02 0.36 5.84 6.41 6.62 6.81 7.32 500 1.01
mu[8] 7.33 0.02 0.42 6.41 7.09 7.34 7.58 8.1 500 1.02
mu[9] 8.06 0.02 0.5 6.98 7.77 8.08 8.37 8.98 500 1.02
mu[10] 8.79 0.03 0.58 7.54 8.43 8.81 9.16 9.85 500 1.02
lp__ -3.59 0.08 1.87 -8.62 -4.54 -3.04 -2.2 -1.48 500 1.0
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:43:19 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
fit.plot(['a', 'b']);
plt.tight_layout()

Simple Logistic model¶
We have observations of height and weight and want to use a logistic model to guess the sex.
# observed data
df = pd.read_csv('HtWt.csv')
df.head()
| male | height | weight | |
|---|---|---|---|
| 0 | 0 | 63.2 | 168.7 |
| 1 | 0 | 68.7 | 169.8 |
| 2 | 0 | 64.8 | 176.6 |
| 3 | 0 | 67.9 | 246.8 |
| 4 | 1 | 68.9 | 151.6 |
log_reg_code = """
data {
int<lower=0> n;
int male[n];
real weight[n];
real height[n];
}
transformed data {}
parameters {
real a;
real b;
real c;
}
transformed parameters {}
model {
a ~ normal(0, 10);
b ~ normal(0, 10);
c ~ normal(0, 10);
for(i in 1:n) {
male[i] ~ bernoulli(inv_logit(a*weight[i] + b*height[i] + c));
}
}
generated quantities {}
"""
log_reg_dat = {
'n': len(df),
'male': df.male,
'height': df.height,
'weight': df.weight
}
fit = pystan.stan(model_code=log_reg_code, data=log_reg_dat, iter=1000, chains=4)
INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_bbf283522d1e199c049bb423b4a6e0da NOW.
fit
Inference for Stan model: anon_model_bbf283522d1e199c049bb423b4a6e0da.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a 9.0e-3 2.2e-4 9.8e-3 -0.01 2.1e-3 9.3e-3 0.02 0.03 2000 1.0
b 0.38 2.0e-3 0.09 0.2 0.32 0.37 0.44 0.56 2000 1.01
c -26.56 0.13 5.95 -38.72 -30.44 -26.31 -22.51 -14.95 2000 1.01
lp__ -35.38 0.03 1.25 -38.66 -36.02 -35.06 -34.44 -33.9 2000 1.01
Samples were drawn using NUTS(diag_e) at Mon Apr 3 23:43:57 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
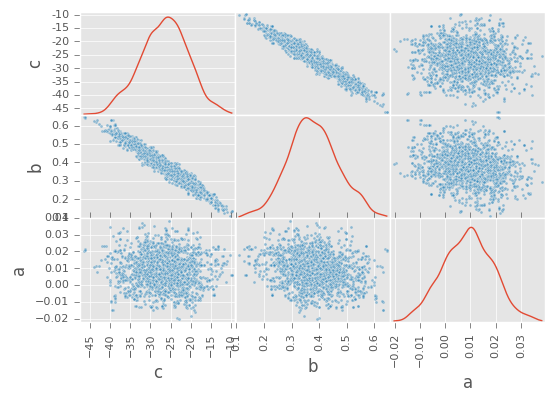
df_trace = pd.DataFrame(fit.extract(['c', 'b', 'a']))
pd.scatter_matrix(df_trace[:], diagonal='kde');