[1]:
%matplotlib inline
import networkx as nx
from networkx.drawing.nx_pydot import graphviz_layout
from networkx.drawing.layout import planar_layout
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
import pandas as pd
import numpy as np
Graph concepts¶
elements¶
graph
vertex
edge
path
graph properties¶
directed or undirected
weighted or unweighted
cyclic or acyclic
single or multiple edges
connected or disconnected
vertex properties¶
in-degree
out-degree
centrality
edge properties¶
direction
weight
multiplicity
Graph representations¶
Vertex and edge collections
Adjacency list
Adjacency matrix
Sparse matrix
[2]:
%matplotlib inline
import networkx as nx
from pprint import pprint
[3]:
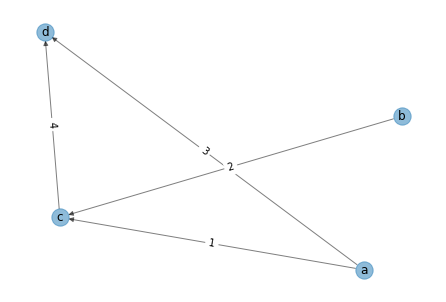
vs = ['a', 'b', 'c', 'd']
es = [('a','c', 1), ('b','c', 2), ('a','d', 3), ('c', 'd', 4)]
g1 = nx.DiGraph()
g1.add_nodes_from(vs)
g1.add_weighted_edges_from(es)
pos = nx.spring_layout(g1)
labels = nx.get_edge_attributes(g1,'weight')
nx.draw(g1, pos=pos, alpha=0.5)
nx.draw_networkx_edge_labels(g1, pos=pos, edge_labels=labels)
nx.draw_networkx_labels(g1, pos=pos)
pass
[4]:
import sys
[5]:
nx.write_adjlist(g1, sys.stdout)
#/usr/local/lib/python3.8/site-packages/ipykernel_launcher.py -f /Users/cliburnchan/Library/Jupyter/runtime/kernel-cbc7a826-65d9-4be6-993f-cecdb1c227ba.json
# GMT Thu Nov 12 00:34:55 2020
#
a c d
b c
c d
d
[6]:
print(nx.adj_matrix(g1))
(0, 2) 1
(0, 3) 3
(1, 2) 2
(2, 3) 4
[7]:
nx.adj_matrix(g1).todense()
[7]:
matrix([[0, 0, 1, 3],
[0, 0, 2, 0],
[0, 0, 0, 4],
[0, 0, 0, 0]])
[8]:
#### Standard format for graph exchange is GraphML
[9]:
nx.write_gml(g1, sys.stdout)
graph [
directed 1
node [
id 0
label "a"
]
node [
id 1
label "b"
]
node [
id 2
label "c"
]
node [
id 3
label "d"
]
edge [
source 0
target 2
weight 1
]
edge [
source 0
target 3
weight 3
]
edge [
source 1
target 2
weight 2
]
edge [
source 2
target 3
weight 4
]
]
Some examples¶
[10]:
n = 50
k = 6
p =0.3
g = nx.watts_strogatz_graph(n, k, p)
Graph Algorithms¶
[16]:
! python3 -m pip install --quiet pydot python-louvain
Search¶
[17]:
g = {
1: [2,3,4],
2: [5,6],
3: [],
4: [7,8],
5: [9,10],
6: [],
7: [11, 12],
8: [],
9: [],
10: [],
11: [],
12: []
}
[18]:
G = nx.from_dict_of_lists(g)
[19]:
pos = graphviz_layout(G, prog='dot')
[20]:
nx.draw(G, pos, with_labels=True, node_size=600, node_color='lightblue')
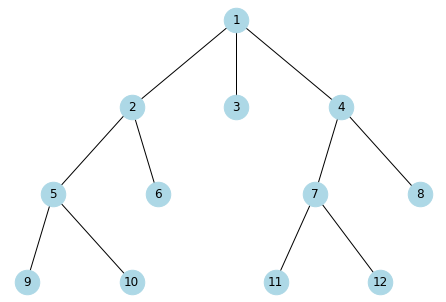
Pathfinding¶
[23]:
edges = [
('A', 'B', 8),
('A', 'C', 5),
('A', 'D', 1),
('B', 'C', 6),
('C', 'D', 3),
('C', 'E', 2),
('D', 'E', 4)
]
[24]:
G = nx.Graph()
G.add_weighted_edges_from(edges)
[25]:
pos = planar_layout(G)
nx.draw(G,
pos,
with_labels=True,
node_size=600,
node_color='lightblue')
labels = nx.draw_networkx_edge_labels(
G,
pos,
edge_labels={(x[0], x[1]): str(x[2]) for x in edges},
font_size=15,
)
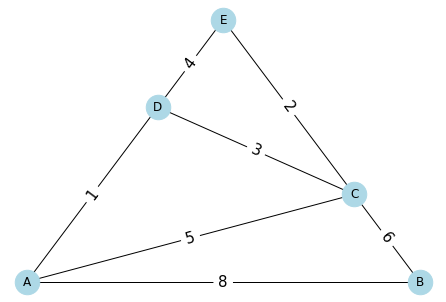
Single source shortest path¶
[27]:
list(nx.single_source_dijkstra(G, 'A'))
[27]:
[{'A': 0, 'D': 1, 'C': 4, 'E': 5, 'B': 8},
{'A': ['A'],
'B': ['A', 'B'],
'C': ['A', 'D', 'C'],
'D': ['A', 'D'],
'E': ['A', 'D', 'E']}]
All pairs shortest path¶
[28]:
list(nx.all_pairs_dijkstra_path(G))
[28]:
[('A',
{'A': ['A'],
'B': ['A', 'B'],
'C': ['A', 'D', 'C'],
'D': ['A', 'D'],
'E': ['A', 'D', 'E']}),
('B',
{'B': ['B'],
'A': ['B', 'A'],
'C': ['B', 'C'],
'D': ['B', 'C', 'D'],
'E': ['B', 'C', 'E']}),
('C',
{'C': ['C'],
'A': ['C', 'D', 'A'],
'B': ['C', 'B'],
'D': ['C', 'D'],
'E': ['C', 'E']}),
('D',
{'D': ['D'],
'A': ['D', 'A'],
'C': ['D', 'C'],
'E': ['D', 'E'],
'B': ['D', 'A', 'B']}),
('E',
{'E': ['E'],
'C': ['E', 'C'],
'D': ['E', 'D'],
'A': ['E', 'D', 'A'],
'B': ['E', 'C', 'B']})]
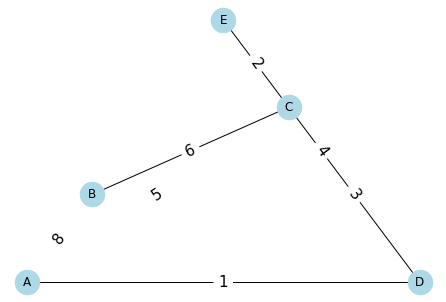
Minimal spanning tree¶
[29]:
G_min = nx.minimum_spanning_tree(G)
[30]:
pos = planar_layout(G_min)
nx.draw(G_min,
pos,
with_labels=True,
node_size=600,
node_color='lightblue')
labels = nx.draw_networkx_edge_labels(
G_min,
pos,
edge_labels={(x[0], x[1]): str(x[2]) for x in edges},
font_size=15,
)
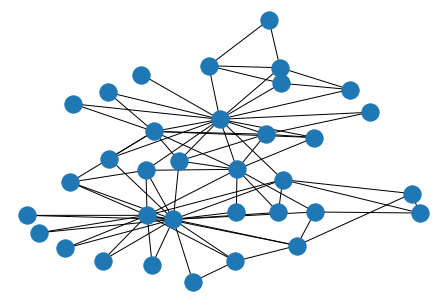
Centrality¶
[31]:
G = nx.karate_club_graph()
[32]:
pos = nx.kamada_kawai_layout(G)
[33]:
nx.draw(G, pos)
[34]:
plt.viridis()
<Figure size 432x288 with 0 Axes>
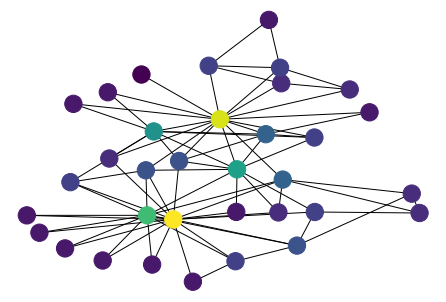
[35]:
values = nx.degree(G)
n_color = np.asarray([values(n) for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
[36]:
help(nx.closeness_centrality)
Help on function closeness_centrality in module networkx.algorithms.centrality.closeness:
closeness_centrality(G, u=None, distance=None, wf_improved=True)
Compute closeness centrality for nodes.
Closeness centrality [1]_ of a node `u` is the reciprocal of the
average shortest path distance to `u` over all `n-1` reachable nodes.
.. math::
C(u) = \frac{n - 1}{\sum_{v=1}^{n-1} d(v, u)},
where `d(v, u)` is the shortest-path distance between `v` and `u`,
and `n` is the number of nodes that can reach `u`. Notice that the
closeness distance function computes the incoming distance to `u`
for directed graphs. To use outward distance, act on `G.reverse()`.
Notice that higher values of closeness indicate higher centrality.
Wasserman and Faust propose an improved formula for graphs with
more than one connected component. The result is "a ratio of the
fraction of actors in the group who are reachable, to the average
distance" from the reachable actors [2]_. You might think this
scale factor is inverted but it is not. As is, nodes from small
components receive a smaller closeness value. Letting `N` denote
the number of nodes in the graph,
.. math::
C_{WF}(u) = \frac{n-1}{N-1} \frac{n - 1}{\sum_{v=1}^{n-1} d(v, u)},
Parameters
----------
G : graph
A NetworkX graph
u : node, optional
Return only the value for node u
distance : edge attribute key, optional (default=None)
Use the specified edge attribute as the edge distance in shortest
path calculations
wf_improved : bool, optional (default=True)
If True, scale by the fraction of nodes reachable. This gives the
Wasserman and Faust improved formula. For single component graphs
it is the same as the original formula.
Returns
-------
nodes : dictionary
Dictionary of nodes with closeness centrality as the value.
See Also
--------
betweenness_centrality, load_centrality, eigenvector_centrality,
degree_centrality, incremental_closeness_centrality
Notes
-----
The closeness centrality is normalized to `(n-1)/(|G|-1)` where
`n` is the number of nodes in the connected part of graph
containing the node. If the graph is not completely connected,
this algorithm computes the closeness centrality for each
connected part separately scaled by that parts size.
If the 'distance' keyword is set to an edge attribute key then the
shortest-path length will be computed using Dijkstra's algorithm with
that edge attribute as the edge weight.
The closeness centrality uses *inward* distance to a node, not outward.
If you want to use outword distances apply the function to `G.reverse()`
In NetworkX 2.2 and earlier a bug caused Dijkstra's algorithm to use the
outward distance rather than the inward distance. If you use a 'distance'
keyword and a DiGraph, your results will change between v2.2 and v2.3.
References
----------
.. [1] Linton C. Freeman: Centrality in networks: I.
Conceptual clarification. Social Networks 1:215-239, 1979.
http://leonidzhukov.ru/hse/2013/socialnetworks/papers/freeman79-centrality.pdf
.. [2] pg. 201 of Wasserman, S. and Faust, K.,
Social Network Analysis: Methods and Applications, 1994,
Cambridge University Press.
[37]:
values = nx.closeness_centrality(G)
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)

[38]:
help(nx.pagerank)
Help on function pagerank in module networkx.algorithms.link_analysis.pagerank_alg:
pagerank(G, alpha=0.85, personalization=None, max_iter=100, tol=1e-06, nstart=None, weight='weight', dangling=None)
Returns the PageRank of the nodes in the graph.
PageRank computes a ranking of the nodes in the graph G based on
the structure of the incoming links. It was originally designed as
an algorithm to rank web pages.
Parameters
----------
G : graph
A NetworkX graph. Undirected graphs will be converted to a directed
graph with two directed edges for each undirected edge.
alpha : float, optional
Damping parameter for PageRank, default=0.85.
personalization: dict, optional
The "personalization vector" consisting of a dictionary with a
key some subset of graph nodes and personalization value each of those.
At least one personalization value must be non-zero.
If not specfiied, a nodes personalization value will be zero.
By default, a uniform distribution is used.
max_iter : integer, optional
Maximum number of iterations in power method eigenvalue solver.
tol : float, optional
Error tolerance used to check convergence in power method solver.
nstart : dictionary, optional
Starting value of PageRank iteration for each node.
weight : key, optional
Edge data key to use as weight. If None weights are set to 1.
dangling: dict, optional
The outedges to be assigned to any "dangling" nodes, i.e., nodes without
any outedges. The dict key is the node the outedge points to and the dict
value is the weight of that outedge. By default, dangling nodes are given
outedges according to the personalization vector (uniform if not
specified). This must be selected to result in an irreducible transition
matrix (see notes under google_matrix). It may be common to have the
dangling dict to be the same as the personalization dict.
Returns
-------
pagerank : dictionary
Dictionary of nodes with PageRank as value
Examples
--------
>>> G = nx.DiGraph(nx.path_graph(4))
>>> pr = nx.pagerank(G, alpha=0.9)
Notes
-----
The eigenvector calculation is done by the power iteration method
and has no guarantee of convergence. The iteration will stop after
an error tolerance of ``len(G) * tol`` has been reached. If the
number of iterations exceed `max_iter`, a
:exc:`networkx.exception.PowerIterationFailedConvergence` exception
is raised.
The PageRank algorithm was designed for directed graphs but this
algorithm does not check if the input graph is directed and will
execute on undirected graphs by converting each edge in the
directed graph to two edges.
See Also
--------
pagerank_numpy, pagerank_scipy, google_matrix
Raises
------
PowerIterationFailedConvergence
If the algorithm fails to converge to the specified tolerance
within the specified number of iterations of the power iteration
method.
References
----------
.. [1] A. Langville and C. Meyer,
"A survey of eigenvector methods of web information retrieval."
http://citeseer.ist.psu.edu/713792.html
.. [2] Page, Lawrence; Brin, Sergey; Motwani, Rajeev and Winograd, Terry,
The PageRank citation ranking: Bringing order to the Web. 1999
http://dbpubs.stanford.edu:8090/pub/showDoc.Fulltext?lang=en&doc=1999-66&format=pdf
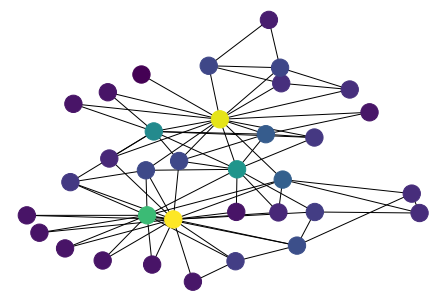
[39]:
values = nx.pagerank(G)
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
Community Detection¶
Triangles¶
[40]:
help(nx.triangles)
Help on function triangles in module networkx.algorithms.cluster:
triangles(G, nodes=None)
Compute the number of triangles.
Finds the number of triangles that include a node as one vertex.
Parameters
----------
G : graph
A networkx graph
nodes : container of nodes, optional (default= all nodes in G)
Compute triangles for nodes in this container.
Returns
-------
out : dictionary
Number of triangles keyed by node label.
Examples
--------
>>> G = nx.complete_graph(5)
>>> print(nx.triangles(G, 0))
6
>>> print(nx.triangles(G))
{0: 6, 1: 6, 2: 6, 3: 6, 4: 6}
>>> print(list(nx.triangles(G, (0, 1)).values()))
[6, 6]
Notes
-----
When computing triangles for the entire graph each triangle is counted
three times, once at each node. Self loops are ignored.
[41]:
values = nx.triangles(G)
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
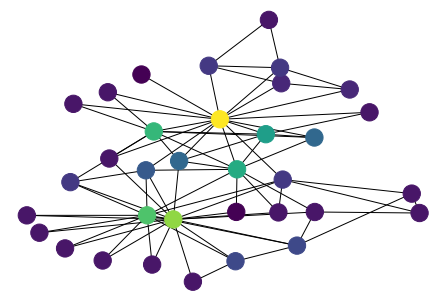
Clustering coefficient¶
[42]:
help(nx.clustering)
Help on function clustering in module networkx.algorithms.cluster:
clustering(G, nodes=None, weight=None)
Compute the clustering coefficient for nodes.
For unweighted graphs, the clustering of a node :math:`u`
is the fraction of possible triangles through that node that exist,
.. math::
c_u = \frac{2 T(u)}{deg(u)(deg(u)-1)},
where :math:`T(u)` is the number of triangles through node :math:`u` and
:math:`deg(u)` is the degree of :math:`u`.
For weighted graphs, there are several ways to define clustering [1]_.
the one used here is defined
as the geometric average of the subgraph edge weights [2]_,
.. math::
c_u = \frac{1}{deg(u)(deg(u)-1))}
\sum_{vw} (\hat{w}_{uv} \hat{w}_{uw} \hat{w}_{vw})^{1/3}.
The edge weights :math:`\hat{w}_{uv}` are normalized by the maximum weight
in the network :math:`\hat{w}_{uv} = w_{uv}/\max(w)`.
The value of :math:`c_u` is assigned to 0 if :math:`deg(u) < 2`.
For directed graphs, the clustering is similarly defined as the fraction
of all possible directed triangles or geometric average of the subgraph
edge weights for unweighted and weighted directed graph respectively [3]_.
.. math::
c_u = \frac{1}{deg^{tot}(u)(deg^{tot}(u)-1) - 2deg^{\leftrightarrow}(u)}
T(u),
where :math:`T(u)` is the number of directed triangles through node
:math:`u`, :math:`deg^{tot}(u)` is the sum of in degree and out degree of
:math:`u` and :math:`deg^{\leftrightarrow}(u)` is the reciprocal degree of
:math:`u`.
Parameters
----------
G : graph
nodes : container of nodes, optional (default=all nodes in G)
Compute clustering for nodes in this container.
weight : string or None, optional (default=None)
The edge attribute that holds the numerical value used as a weight.
If None, then each edge has weight 1.
Returns
-------
out : float, or dictionary
Clustering coefficient at specified nodes
Examples
--------
>>> G = nx.complete_graph(5)
>>> print(nx.clustering(G, 0))
1.0
>>> print(nx.clustering(G))
{0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0, 4: 1.0}
Notes
-----
Self loops are ignored.
References
----------
.. [1] Generalizations of the clustering coefficient to weighted
complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela,
K. Kaski, and J. Kertész, Physical Review E, 75 027105 (2007).
http://jponnela.com/web_documents/a9.pdf
.. [2] Intensity and coherence of motifs in weighted complex
networks by J. P. Onnela, J. Saramäki, J. Kertész, and K. Kaski,
Physical Review E, 71(6), 065103 (2005).
.. [3] Clustering in complex directed networks by G. Fagiolo,
Physical Review E, 76(2), 026107 (2007).
[43]:
values = nx.clustering(G)
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
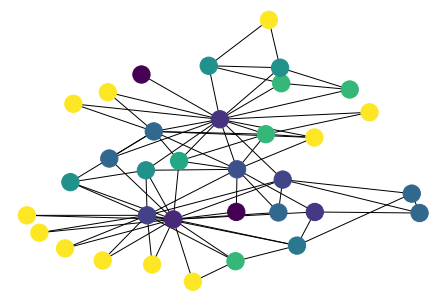
[44]:
import matplotlib.colors as mcolors
[45]:
colors = list(mcolors.BASE_COLORS.keys())
Label propagation¶
[46]:
help(nx.community.label_propagation_communities)
Help on function label_propagation_communities in module networkx.algorithms.community.label_propagation:
label_propagation_communities(G)
Generates community sets determined by label propagation
Finds communities in `G` using a semi-synchronous label propagation
method[1]_. This method combines the advantages of both the synchronous
and asynchronous models. Not implemented for directed graphs.
Parameters
----------
G : graph
An undirected NetworkX graph.
Yields
------
communities : generator
Yields sets of the nodes in each community.
Raises
------
NetworkXNotImplemented
If the graph is directed
References
----------
.. [1] Cordasco, G., & Gargano, L. (2010, December). Community detection
via semi-synchronous label propagation algorithms. In Business
Applications of Social Network Analysis (BASNA), 2010 IEEE International
Workshop on (pp. 1-8). IEEE.
[47]:
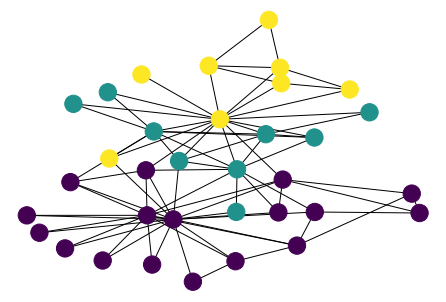
parts = list(nx.community.label_propagation_communities(G))
values = {n: i for i, ns in enumerate(parts) for n in ns}
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
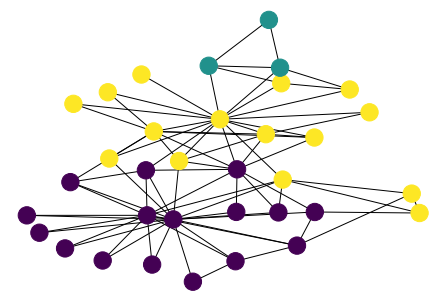
Clauset-Newman-Moore greedy modularity¶
Definition - Modularity is the fraction of the edges that fall within the given groups minus the expected fraction if edges were distributed at random.
[48]:
help(nx.community.greedy_modularity_communities)
Help on function greedy_modularity_communities in module networkx.algorithms.community.modularity_max:
greedy_modularity_communities(G, weight=None)
Find communities in graph using Clauset-Newman-Moore greedy modularity
maximization. This method currently supports the Graph class and does not
consider edge weights.
Greedy modularity maximization begins with each node in its own community
and joins the pair of communities that most increases modularity until no
such pair exists.
Parameters
----------
G : NetworkX graph
Returns
-------
Yields sets of nodes, one for each community.
Examples
--------
>>> from networkx.algorithms.community import greedy_modularity_communities
>>> G = nx.karate_club_graph()
>>> c = list(greedy_modularity_communities(G))
>>> sorted(c[0])
[8, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]
References
----------
.. [1] M. E. J Newman 'Networks: An Introduction', page 224
Oxford University Press 2011.
.. [2] Clauset, A., Newman, M. E., & Moore, C.
"Finding community structure in very large networks."
Physical Review E 70(6), 2004.
[49]:
parts = list(nx.community.greedy_modularity_communities(G))
values = {n: i for i, ns in enumerate(parts) for n in ns}
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)
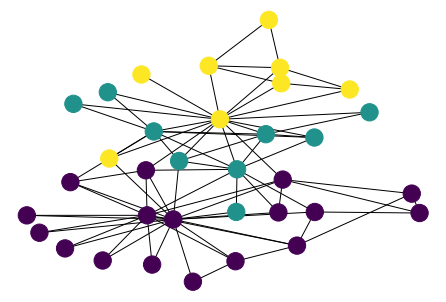
Louvain¶
This works well on large graphs, and is used to cluster single-cell RNA-seq data into cell subsets.
[50]:
import community as community_louvain
[51]:
help(community_louvain.best_partition)
Help on function best_partition in module community.community_louvain:
best_partition(graph, partition=None, weight='weight', resolution=1.0, randomize=None, random_state=None)
Compute the partition of the graph nodes which maximises the modularity
(or try..) using the Louvain heuristices
This is the partition of highest modularity, i.e. the highest partition
of the dendrogram generated by the Louvain algorithm.
Parameters
----------
graph : networkx.Graph
the networkx graph which is decomposed
partition : dict, optional
the algorithm will start using this partition of the nodes.
It's a dictionary where keys are their nodes and values the communities
weight : str, optional
the key in graph to use as weight. Default to 'weight'
resolution : double, optional
Will change the size of the communities, default to 1.
represents the time described in
"Laplacian Dynamics and Multiscale Modular Structure in Networks",
R. Lambiotte, J.-C. Delvenne, M. Barahona
randomize : boolean, optional
Will randomize the node evaluation order and the community evaluation
order to get different partitions at each call
random_state : int, RandomState instance or None, optional (default=None)
If int, random_state is the seed used by the random number generator;
If RandomState instance, random_state is the random number generator;
If None, the random number generator is the RandomState instance used
by `np.random`.
Returns
-------
partition : dictionnary
The partition, with communities numbered from 0 to number of communities
Raises
------
NetworkXError
If the graph is not Eulerian.
See Also
--------
generate_dendrogram to obtain all the decompositions levels
Notes
-----
Uses Louvain algorithm
References
----------
.. 1. Blondel, V.D. et al. Fast unfolding of communities in
large networks. J. Stat. Mech 10008, 1-12(2008).
Examples
--------
>>> #Basic usage
>>> G=nx.erdos_renyi_graph(100, 0.01)
>>> part = best_partition(G)
>>> #other example to display a graph with its community :
>>> #better with karate_graph() as defined in networkx examples
>>> #erdos renyi don't have true community structure
>>> G = nx.erdos_renyi_graph(30, 0.05)
>>> #first compute the best partition
>>> partition = community.best_partition(G)
>>> #drawing
>>> size = float(len(set(partition.values())))
>>> pos = nx.spring_layout(G)
>>> count = 0.
>>> for com in set(partition.values()) :
>>> count += 1.
>>> list_nodes = [nodes for nodes in partition.keys()
>>> if partition[nodes] == com]
>>> nx.draw_networkx_nodes(G, pos, list_nodes, node_size = 20,
node_color = str(count / size))
>>> nx.draw_networkx_edges(G, pos, alpha=0.5)
>>> plt.show()
[52]:
partion = community_louvain.best_partition(G)
values = {n: i for i, ns in enumerate(parts) for n in ns}
n_color = np.asarray([values[n] for n in G.nodes()])
nx.draw(G, pos, node_color=n_color)