Using optimization routines from scipy and statsmodels¶
[1]:
%matplotlib inline
[2]:
import scipy.linalg as la
import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt
import pandas as pd
[3]:
np.set_printoptions(precision=3, suppress=True)
Using scipy.optimize¶
One of the most convenient libraries to use is scipy.optimize, since it is already part of the Anaconda installation and it has a fairly intuitive interface.
[35]:
from scipy import optimize as opt
Minimizing a univariate function \(f: \mathbb{R} \rightarrow \mathbb{R}\)¶
[36]:
def f(x):
return x**4 + 3*(x-2)**3 - 15*(x)**2 + 1
[37]:
x = np.linspace(-8, 5, 100)
plt.plot(x, f(x));
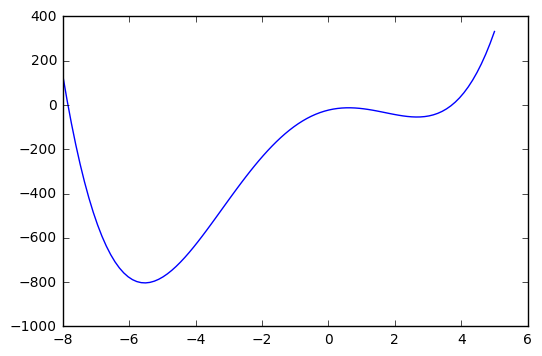
The `minimize_scalar <http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize_scalar.html#scipy.optimize.minimize_scalar>`__ function will find the minimum, and can also be told to search within given bounds. By default, it uses the Brent algorithm, which combines a bracketing strategy with a parabolic approximation.
[38]:
opt.minimize_scalar(f, method='Brent')
[38]:
fun: -803.39553088258845
nfev: 12
nit: 11
success: True
x: -5.5288011252196627
[39]:
opt.minimize_scalar(f, method='bounded', bounds=[0, 6])
[39]:
fun: -54.210039377127622
message: 'Solution found.'
nfev: 12
status: 0
success: True
x: 2.6688651040396532
Local and global minima¶
[40]:
def f(x, offset):
return -np.sinc(x-offset)
[41]:
x = np.linspace(-20, 20, 100)
plt.plot(x, f(x, 5));
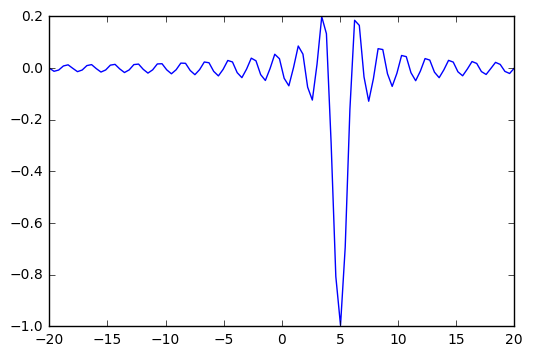
[42]:
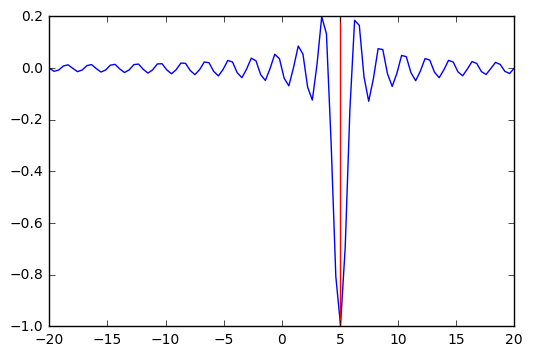
# note how additional function arguments are passed in
sol = opt.minimize_scalar(f, args=(5,))
sol
[42]:
fun: -0.049029624014074166
nfev: 11
nit: 10
success: True
x: -1.4843871263953001
[43]:
plt.plot(x, f(x, 5))
plt.axvline(sol.x, c='red')
pass
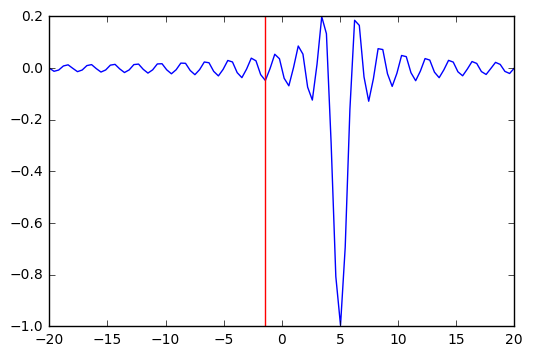
We can try multiple random starts to find the global minimum¶
[44]:
lower = np.random.uniform(-20, 20, 100)
upper = lower + 1
sols = [opt.minimize_scalar(f, args=(5,), bracket=(l, u)) for (l, u) in zip(lower, upper)]
[45]:
idx = np.argmin([sol.fun for sol in sols])
sol = sols[idx]
[46]:
plt.plot(x, f(x, 5))
plt.axvline(sol.x, c='red');
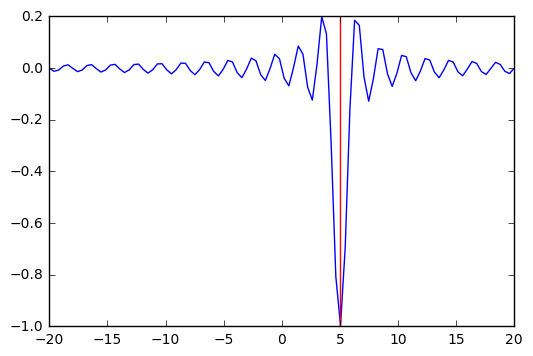
Using a stochastic algorithm¶
See documentation for the `basinhopping <http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.optimize.basinhopping.html>`__ algorithm, which also works with multivariate scalar optimization. Note that this is heuristic and not guaranteed to find a global minimum.
[47]:
from scipy.optimize import basinhopping
x0 = 0
sol = basinhopping(f, x0, stepsize=1, minimizer_kwargs={'args': (5,)})
sol
[47]:
fun: -1.0
lowest_optimization_result: fun: -1.0
hess_inv: array([[ 0.304]])
jac: array([ 0.])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([ 5.])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 1848
nit: 100
njev: 616
x: array([ 5.])
[48]:
plt.plot(x, f(x, 5))
plt.axvline(sol.x, c='red');
Constrained optimization with scipy.optimize¶
Many real-world optimization problems have constraints - for example, a set of parameters may have to sum to 1.0 (equality constraint), or some parameters may have to be non-negative (inequality constraint). Sometimes, the constraints can be incorporated into the function to be minimized, for example, the non-negativity constraint \(p \gt 0\) can be removed by substituting \(p = e^q\) and optimizing for \(q\). Using such workarounds, it may be possible to convert a constrained optimization problem into an unconstrained one, and use the methods discussed above to solve the problem.
Alternatively, we can use optimization methods that allow the specification of constraints directly in the problem statement as shown in this section. Internally, constraint violation penalties, barriers and Lagrange multipliers are some of the methods used used to handle these constraints. We use the example provided in the Scipy tutorial to illustrate how to set constraints.
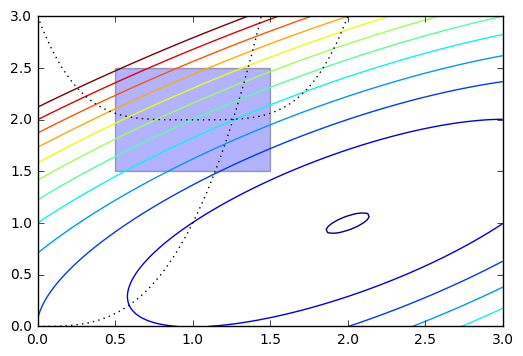
We will optimize:
[83]:
def f(x):
return -(2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2)
[84]:
x = np.linspace(0, 3, 100)
y = np.linspace(0, 3, 100)
X, Y = np.meshgrid(x, y)
Z = f(np.vstack([X.ravel(), Y.ravel()])).reshape((100,100))
plt.contour(X, Y, Z, np.arange(-1.99,10, 1), cmap='jet');
plt.plot(x, x**3, 'k:', linewidth=1)
plt.plot(x, (x-1)**4+2, 'k:', linewidth=1)
plt.fill([0.5,0.5,1.5,1.5], [2.5,1.5,1.5,2.5], alpha=0.3)
plt.axis([0,3,0,3])
[84]:
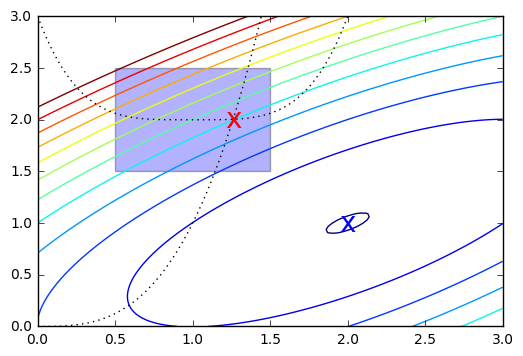
To set constraints, we pass in a dictionary with keys type, fun and jac. Note that the inequality constraint assumes a \(C_j x \ge 0\) form. As usual, the jac is optional and will be numerically estimated if not provided.
[85]:
cons = ({'type': 'eq',
'fun' : lambda x: np.array([x[0]**3 - x[1]]),
'jac' : lambda x: np.array([3.0*(x[0]**2.0), -1.0])},
{'type': 'ineq',
'fun' : lambda x: np.array([x[1] - (x[0]-1)**4 - 2])})
bnds = ((0.5, 1.5), (1.5, 2.5))
[86]:
x0 = [0, 2.5]
Unconstrained optimization
[87]:
ux = opt.minimize(f, x0, constraints=None)
ux
[87]:
fun: -1.9999999999996365
hess_inv: array([[ 0.998, 0.501],
[ 0.501, 0.499]])
jac: array([ 0., -0.])
message: 'Optimization terminated successfully.'
nfev: 24
nit: 5
njev: 6
status: 0
success: True
x: array([ 2., 1.])
Constrained optimization
[88]:
cx = opt.minimize(f, x0, bounds=bnds, constraints=cons)
cx
[88]:
fun: 2.0499154720910759
jac: array([-3.487, 5.497, 0. ])
message: 'Optimization terminated successfully.'
nfev: 21
nit: 5
njev: 5
status: 0
success: True
x: array([ 1.261, 2.005])
[89]:
x = np.linspace(0, 3, 100)
y = np.linspace(0, 3, 100)
X, Y = np.meshgrid(x, y)
Z = f(np.vstack([X.ravel(), Y.ravel()])).reshape((100,100))
plt.contour(X, Y, Z, np.arange(-1.99,10, 1), cmap='jet');
plt.plot(x, x**3, 'k:', linewidth=1)
plt.plot(x, (x-1)**4+2, 'k:', linewidth=1)
plt.text(ux['x'][0], ux['x'][1], 'x', va='center', ha='center', size=20, color='blue')
plt.text(cx['x'][0], cx['x'][1], 'x', va='center', ha='center', size=20, color='red')
plt.fill([0.5,0.5,1.5,1.5], [2.5,1.5,1.5,2.5], alpha=0.3)
plt.axis([0,3,0,3]);
Some applications of optimization¶
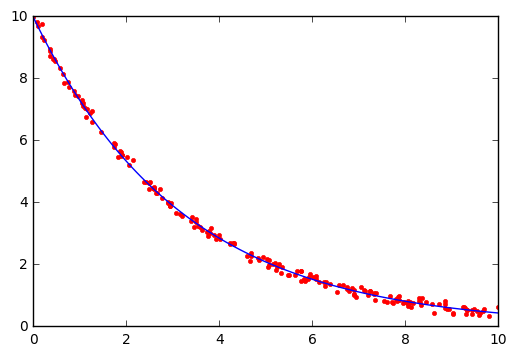
This is a specialized application of curve_fit, in which the curve to be fitted is defined implicitly by an ordinary differential equation
A more elaborate example for fitting a system of ODEs to model the zombie apocalypse
[96]:
from scipy.integrate import odeint
def f(x, t, k):
"""Simple exponential decay."""
return -k*x
def x(t, k, x0):
"""
Solution to the ODE x'(t) = f(t,x,k) with initial condition x(0) = x0
"""
x = odeint(f, x0, t, args=(k,))
return x.ravel()
[97]:
# True parameter values
x0_ = 10
k_ = 0.1*np.pi
# Some random data genererated from closed form solution plus Gaussian noise
ts = np.sort(np.random.uniform(0, 10, 200))
xs = x0_*np.exp(-k_*ts) + np.random.normal(0,0.1,200)
popt, cov = curve_fit(x, ts, xs)
k_opt, x0_opt = popt
print("k = %g" % k_opt)
print("x0 = %g" % x0_opt)
k = 0.313527
x0 = 9.97788
[98]:
import matplotlib.pyplot as plt
t = np.linspace(0, 10, 100)
plt.plot(ts, xs, 'r.', t, x(t, k_opt, x0_opt), '-');
You may have to install the `lmfit <http://cars9.uchicago.edu/software/python/lmfit/index.html>`__ package using pip and restart your kernel. The lmfit algorithm is another wrapper around scipy.optimize.leastsq but allows for richer model specification and more diagnostics.
[99]:
! pip install lmfit
Requirement already satisfied (use --upgrade to upgrade): lmfit in /opt/conda/lib/python3.5/site-packages
Requirement already satisfied (use --upgrade to upgrade): scipy in /opt/conda/lib/python3.5/site-packages (from lmfit)
Requirement already satisfied (use --upgrade to upgrade): numpy in /opt/conda/lib/python3.5/site-packages (from lmfit)
You are using pip version 8.1.2, however version 9.0.1 is available.
You should consider upgrading via the 'pip install --upgrade pip' command.
[100]:
from lmfit import minimize, Parameters, Parameter, report_fit
import warnings
[101]:
def f(xs, t, ps):
"""Lotka-Volterra predator-prey model."""
try:
a = ps['a'].value
b = ps['b'].value
c = ps['c'].value
d = ps['d'].value
except:
a, b, c, d = ps
x, y = xs
return [a*x - b*x*y, c*x*y - d*y]
def g(t, x0, ps):
"""
Solution to the ODE x'(t) = f(t,x,k) with initial condition x(0) = x0
"""
x = odeint(f, x0, t, args=(ps,))
return x
def residual(ps, ts, data):
x0 = ps['x0'].value, ps['y0'].value
model = g(ts, x0, ps)
return (model - data).ravel()
t = np.linspace(0, 10, 100)
x0 = np.array([1,1])
a, b, c, d = 3,1,1,1
true_params = np.array((a, b, c, d))
np.random.seed(123)
data = g(t, x0, true_params)
data += np.random.normal(size=data.shape)
# set parameters incluing bounds
params = Parameters()
params.add('x0', value= float(data[0, 0]), min=0, max=10)
params.add('y0', value=float(data[0, 1]), min=0, max=10)
params.add('a', value=2.0, min=0, max=10)
params.add('b', value=2.0, min=0, max=10)
params.add('c', value=2.0, min=0, max=10)
params.add('d', value=2.0, min=0, max=10)
# fit model and find predicted values
result = minimize(residual, params, args=(t, data), method='leastsq')
final = data + result.residual.reshape(data.shape)
# plot data and fitted curves
plt.plot(t, data, 'o')
plt.plot(t, final, '-', linewidth=2);
# display fitted statistics
report_fit(result)
/opt/conda/lib/python3.5/site-packages/ipykernel/__main__.py:4: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
[[Fit Statistics]]
# function evals = 147
# data points = 200
# variables = 6
chi-square = 212.716
reduced chi-square = 1.096
Akaike info crit = 24.328
Bayesian info crit = 44.118
[[Variables]]
x0: 1.02060369 +/- 0.181678 (17.80%) (init= 0)
y0: 1.07048852 +/- 0.110177 (10.29%) (init= 1.997345)
a: 3.54326836 +/- 0.454087 (12.82%) (init= 2)
b: 1.21275230 +/- 0.148458 (12.24%) (init= 2)
c: 0.84528522 +/- 0.079480 (9.40%) (init= 2)
d: 0.85717177 +/- 0.085645 (9.99%) (init= 2)
[[Correlations]] (unreported correlations are < 0.100)
C(a, b) = 0.960
C(a, d) = -0.956
C(b, d) = -0.878
C(x0, b) = -0.759
C(x0, a) = -0.745
C(y0, c) = -0.717
C(y0, d) = -0.682
C(c, d) = 0.667
C(x0, d) = 0.578
C(a, c) = -0.532
C(y0, a) = 0.475
C(b, c) = -0.434
C(y0, b) = 0.271
Optimization of graph node placement¶
To show the many different applications of optimization, here is an example using optimization to change the layout of nodes of a graph. We use a physical analogy - nodes are connected by springs, and the springs resist deformation from their natural length \(l_{ij}\). Some nodes are pinned to their initial locations while others are free to move. Because the initial configuration of nodes does not have springs at their natural length, there is tension resulting in a high potential energy \(U\), given by the physics formula shown below. Optimization finds the configuration of lowest potential energy given that some nodes are fixed (set up as boundary constraints on the positions of the nodes).
Note that the ordination algorithm Multi-Dimensional Scaling (MDS) works on a very similar idea - take a high dimensional data set in \(\mathbb{R}^n\), and project down to a lower dimension (\(\mathbb{R}^k\)) such that the sum of distances \(d_n(x_i, x_j) - d_k(x_i, x_j)\), where \(d_n\) and \(d_k\) are some measure of distance between two points \(x_i\) and \(x_j\) in \(n\) and \(d\) dimension respectively, is minimized. MDS is often used in exploratory analysis of high-dimensional data to get some intuitive understanding of its “structure”.
[102]:
from scipy.spatial.distance import pdist, squareform
P0 is the initial location of nodes
P is the minimal energy location of nodes given constraints
A is a connectivity matrix - there is a spring between \(i\) and \(j\) if \(A_{ij} = 1\)
\(L_{ij}\) is the resting length of the spring connecting \(i\) and \(j\)
In addition, there are a number of
fixednodes whose positions are pinned.
[103]:
n = 20
k = 1 # spring stiffness
P0 = np.random.uniform(0, 5, (n,2))
A = np.ones((n, n))
A[np.tril_indices_from(A)] = 0
L = A.copy()
[104]:
L.astype('int')
[104]:
array([[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
[105]:
def energy(P):
P = P.reshape((-1, 2))
D = squareform(pdist(P))
return 0.5*(k * A * (D - L)**2).sum()
[106]:
D0 = squareform(pdist(P0))
E0 = 0.5* k * A * (D0 - L)**2
[107]:
D0[:5, :5]
[107]:
array([[ 0. , 5.039, 0.921, 1.758, 1.99 ],
[ 5.039, 0. , 5.546, 3.414, 4.965],
[ 0.921, 5.546, 0. , 2.133, 2.888],
[ 1.758, 3.414, 2.133, 0. , 2.762],
[ 1.99 , 4.965, 2.888, 2.762, 0. ]])
[108]:
E0[:5, :5]
[108]:
array([[ 0. , 8.159, 0.003, 0.288, 0.49 ],
[ 0. , 0. , 10.333, 2.915, 7.862],
[ 0. , 0. , 0. , 0.642, 1.782],
[ 0. , 0. , 0. , 0. , 1.552],
[ 0. , 0. , 0. , 0. , 0. ]])
[109]:
energy(P0.ravel())
[109]:
[110]:
# fix the position of the first few nodes just to show constraints
fixed = 4
bounds = (np.repeat(P0[:fixed,:].ravel(), 2).reshape((-1,2)).tolist() +
[[None, None]] * (2*(n-fixed)))
bounds[:fixed*2+4]
[110]:
[[1.191249528562059, 1.191249528562059],
[4.0389554314507805, 4.0389554314507805],
[4.474891439430058, 4.474891439430058],
[0.216114460398234, 0.216114460398234],
[1.5097341813135952, 1.5097341813135952],
[4.902910992971438, 4.902910992971438],
[2.6975241127686767, 2.6975241127686767],
[3.1315468085492815, 3.1315468085492815],
[None, None],
[None, None],
[None, None],
[None, None]]
[111]:
sol = opt.minimize(energy, P0.ravel(), bounds=bounds)
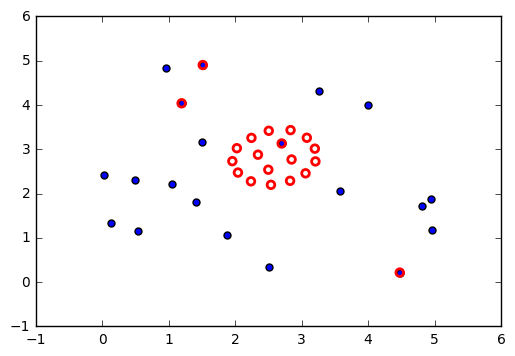
Visualization¶
Original placement is BLUE Optimized arrangement is RED.
[112]:
plt.scatter(P0[:, 0], P0[:, 1], s=25)
P = sol.x.reshape((-1,2))
plt.scatter(P[:, 0], P[:, 1], edgecolors='red', facecolors='none', s=30, linewidth=2);
Optimization of standard statistical models¶
When we solve standard statistical problems, an optimization procedure similar to the ones discussed here is performed. For example, consider multivariate logistic regression - typically, a Newton-like algorithm known as iteratively reweighted least squares (IRLS) is used to find the maximum likelihood estimate for the generalized linear model family. However, using one of the multivariate scalar minimization methods shown above will also work, for example, the BFGS minimization algorithm.
The take home message is that there is nothing magic going on when Python or R fits a statistical model using a formula - all that is happening is that the objective function is set to be the negative of the log likelihood, and the minimum found using some first or second order optimization algorithm.
[113]:
import statsmodels.api as sm
Suppose we have a binary outcome measure \(Y \in {0,1}\) that is conditinal on some input variable (vector) \(x \in (-\infty, +\infty)\). Let the conditioanl probability be \(p(x) = P(Y=y | X=x)\). Given some data, one simple probability model is \(p(x) = \beta_0 + x\cdot\beta\) - i.e. linear regression. This doesn’t really work for the obvious reason that \(p(x)\) must be between 0 and 1 as \(x\) ranges across the real line. One simple way to fix this is to use the transformation \(g(x) = \frac{p(x)}{1 - p(x)} = \beta_0 + x.\beta\). Solving for \(p\), we get
Suppose we have \(n\) data points \((x_i, y_i)\) where \(x_i\) is a vector of features and \(y_i\) is an observed class (0 or 1). For each event, we either have “success” (\(y = 1\)) or “failure” (\(Y = 0\)), so the likelihood looks like the product of Bernoulli random variables. According to the logistic model, the probability of success is \(p(x_i)\) if \(y_i = 1\) and \(1-p(x_i)\) if \(y_i = 0\). So the likelihood is
l(beta_0, beta) &= sum_{i=1}^{n} y_i log{p(x_i)} + (1-y_i)log{1-p(x_i)} \ &= sum_{i=1}^{n} log{1-p(x_i)} + sum_{i=1}^{n} y_i log{frac{p(x_i)}{1-p(x_i)}} \ &= sum_{i=1}^{n} -log 1 + e^{beta_0 + x_icdotbeta} + sum_{i=1}^{n} y_i(beta_0 + x_icdotbeta) end{align}`
Using the standard ‘trick’, if we augment the matrix \(X\) with a column of 1s, we can write \(\beta_0 + x_i\cdot\beta\) as just \(X\beta\).
[114]:
df_ = pd.read_csv("http://www.ats.ucla.edu/stat/data/binary.csv")
df_.head()
[114]:
| admit | gre | gpa | rank | |
|---|---|---|---|---|
| 0 | 0 | 380 | 3.61 | 3 |
| 1 | 1 | 660 | 3.67 | 3 |
| 2 | 1 | 800 | 4.00 | 1 |
| 3 | 1 | 640 | 3.19 | 4 |
| 4 | 0 | 520 | 2.93 | 4 |
[115]:
# We will ignore the rank categorical value
cols_to_keep = ['admit', 'gre', 'gpa']
df = df_[cols_to_keep]
df.insert(1, 'dummy', 1)
df.head()
[115]:
| admit | dummy | gre | gpa | |
|---|---|---|---|---|
| 0 | 0 | 1 | 380 | 3.61 |
| 1 | 1 | 1 | 660 | 3.67 |
| 2 | 1 | 1 | 800 | 4.00 |
| 3 | 1 | 1 | 640 | 3.19 |
| 4 | 0 | 1 | 520 | 2.93 |
This is very similar to what you would do in R, only using Python’s statsmodels package. The GLM solver uses a special variant of Newton’s method known as iteratively reweighted least squares (IRLS), which will be further desribed in the lecture on multivarite and constrained optimizaiton.
[116]:
model = sm.GLM.from_formula('admit ~ gre + gpa',
data=df, family=sm.families.Binomial())
fit = model.fit()
fit.summary()
[116]:
| Dep. Variable: | admit | No. Observations: | 400 |
|---|---|---|---|
| Model: | GLM | Df Residuals: | 397 |
| Model Family: | Binomial | Df Model: | 2 |
| Link Function: | logit | Scale: | 1.0 |
| Method: | IRLS | Log-Likelihood: | -240.17 |
| Date: | Thu, 09 Mar 2017 | Deviance: | 480.34 |
| Time: | 20:12:11 | Pearson chi2: | 398. |
| No. Iterations: | 6 |
| coef | std err | z | P>|z| | [95.0% Conf. Int.] | |
|---|---|---|---|---|---|
| Intercept | -4.9494 | 1.075 | -4.604 | 0.000 | -7.057 -2.842 |
| gre | 0.0027 | 0.001 | 2.544 | 0.011 | 0.001 0.005 |
| gpa | 0.7547 | 0.320 | 2.361 | 0.018 | 0.128 1.381 |
[117]:
%load_ext rpy2.ipython
[118]:
%%R -i df
m <- glm(admit ~ gre + gpa, data=df, family="binomial")
summary(m)
Call:
glm(formula = admit ~ gre + gpa, family = "binomial", data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2730 -0.8988 -0.7206 1.3013 2.0620
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.949378 1.075093 -4.604 4.15e-06 ***
gre 0.002691 0.001057 2.544 0.0109 *
gpa 0.754687 0.319586 2.361 0.0182 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 499.98 on 399 degrees of freedom
Residual deviance: 480.34 on 397 degrees of freedom
AIC: 486.34
Number of Fisher Scoring iterations: 4
This is to show that there is no magic going on - you can write the function to minimize directly from the log-likelihood equation and run a minimizer. It will be more accurate if you also provide the derivative (+/- the Hessian for second order methods), but using just the function and numerical approximations to the derivative will also work. As usual, this is for illustration so you understand what is going on - when there is a library function available, you should probably use that instead.
[119]:
def f(beta, y, x):
"""Minus log likelihood function for logistic regression."""
return -((-np.log(1 + np.exp(np.dot(x, beta)))).sum() + (y*(np.dot(x, beta))).sum())
[120]:
beta0 = np.zeros(3)
opt.minimize(f, beta0, args=(df['admit'], df.ix[:, 'dummy':]), method='BFGS', options={'gtol':1e-2})
[120]:
fun: 240.17199087261878
hess_inv: array([[ 1.115, -0. , -0.27 ],
[-0. , 0. , -0. ],
[-0.27 , -0. , 0.098]])
jac: array([ 0. , -0.002, -0. ])
message: 'Optimization terminated successfully.'
nfev: 65
nit: 8
njev: 13
status: 0
success: True
x: array([-4.949, 0.003, 0.755])
There are also many optimization routines in the scikit-learn package, as you already know from the previous lectures. Many machine learning problems essentially boil down to the minimization of some appropriate loss function.