Line search in gradient and Newton directions

%matplotlib inline

import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar
import numpy as np

Demo functions

def f1(x):
    return x[0]**2 + x[1]**2

def grad1(x):
    return np.array([2*x[0], 2*x[1]]).reshape([-1,1])

def hess1(x):
    return np.array([
        [2, 0],
        [0, 2]
    ])

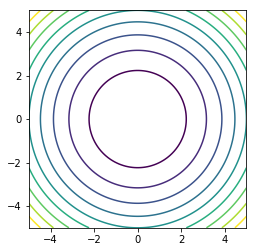
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
plt.contour(X, Y, Z, 10)
plt.axis('square')
pass

np.c_[X.ravel(), Y.ravel()].shape

(10000, 2)

def f2(x):
    return x[0]**2 + 10*x[1]**2

def grad2(x):
    return np.array([2*x[0], 20*x[1]]).reshape([-1,1])

def hess2(x):
    return np.array([
        [2, 0],
        [0, 20]
    ])

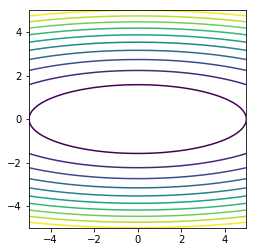
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2
plt.contour(X, Y, Z, 10)
plt.axis('square')
pass

Gradient descent with step size found by numerical minimization

def gd(x, f, grad, max_iter=10):
    orbit = np.zeros((max_iter+1, len(x)))
    orbit[0] = x.ravel()
    for i in range(max_iter):
        res = minimize_scalar(lambda alpha: f(x - alpha * grad(x)))
        alpha = res.x
        x = x - alpha * grad(x)
        orbit[i+1] = x.ravel()
    return orbit

Gradient descent with analytic step size for quadratic function

def gd_alt(x, f, grad, hess, max_iter=10):
    orbit = np.zeros((max_iter+1, len(x)))
    orbit[0] = x.ravel()
    for i in range(max_iter):
        p = -grad(x)
        alpha = (p.T @ p)/(p.T @ hess(x) @ p)
        x = x - alpha * grad(x)
        orbit[i+1] = x.ravel()
    return orbit

x0 = np.array([4,3]).reshape([-1,1])

orbit1 = gd(x0, f1, grad1, max_iter=5)

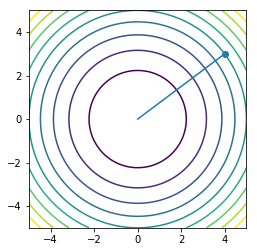
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit1[:, 0], orbit1[:, 1], '-')
plt.scatter(orbit1[0:1, 0], orbit1[0:1, 1])
plt.axis('square')
pass

orbit1a = gd_alt(x0, f1, grad1, hess1, max_iter=5)

/usr/local/lib/python3.6/site-packages/ipykernel_launcher.py:6: RuntimeWarning: invalid value encountered in true_divide

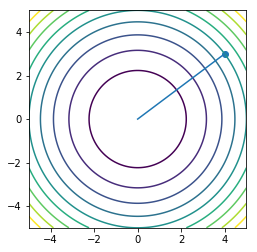
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit1a[:, 0], orbit1a[:, 1], '-')
plt.scatter(orbit1a[0:1, 0], orbit1a[0:1, 1])
plt.axis('square')
pass

orbit2 = gd(x0, f2, grad2, max_iter=5)

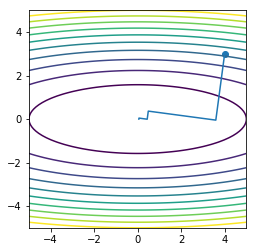
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit2[:, 0], orbit2[:, 1], '-')
plt.scatter(orbit2[0:1, 0], orbit2[0:1, 1])
plt.axis('square')
pass

orbit2a = gd_alt(x0, f2, grad2, hess2, max_iter=5)

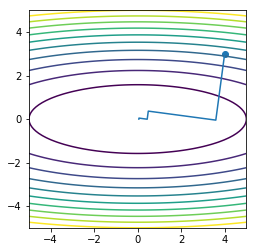
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit2a[:, 0], orbit2a[:, 1], '-')
plt.scatter(orbit2a[0:1, 0], orbit2a[0:1, 1])
plt.axis('square')
pass

Line search in Newton direction with analytic step size

def newton(x, f, grad, hess, max_iter=5):
    orbit = np.zeros((max_iter+1, len(x)))
    orbit[0] = x.ravel()
    for i in range(max_iter):
        x = x - np.linalg.inv(hess(x)) @ grad(x)
        orbit[i+1] = x.ravel()
    return orbit

orbit3 = newton(x0, f1, grad1, hess1, max_iter=5)

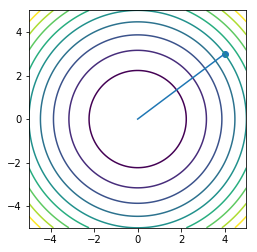
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit3[:, 0], orbit3[:, 1], '-')
plt.scatter(orbit3[0:1, 0], orbit3[0:1, 1])
plt.axis('square')
pass

orbit4 = newton(x0, f2, grad2, hess2, max_iter=5)

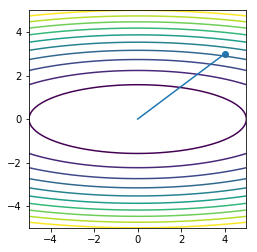
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2
plt.contour(X, Y, Z, 10)
plt.plot(orbit4[:, 0], orbit4[:, 1], '-')
plt.scatter(orbit4[0:1, 0], orbit4[0:1, 1])
plt.axis('square')
pass