In [1]:
%matplotlib inline
import matplotlib.pyplot as plt
Bonus Material: The Humble For Loop¶
Much of numerical computing consists of populating an array of some sort. The general concept is looping, and there is a lot to discover about how to write loops in Python.
(1) Filling a list¶
Using a for loop¶
This is often the most flexible and simplest method to populate a list or array for beginners in Python . Traditionally, the for loop is discouraged in interpreted languages because it is slow. However, the for loop is amenable to JIT compilation that in many cases out-performs the vectorized version.
In [2]:
n = 10
xs = []
for i in range(n):
xs.append(i**2)
xs
Out[2]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Using a list comprehension¶
This is just syntactic sugar for the for loop. If you are writing a pure
python program, list comprehensions and the related generator
expressions, set comprehension, and dictionary comprehension are very
slick. The big disadvantage is that these forms are currently not
supported by the numba JIT compiler.
In [3]:
n = 10
xs = [i**2 for i in range(n)]
xs
Out[3]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Using map¶
This is a “functional” style of writing the for loop, and provides a
higher level of abstraction. As a result, the map function is
generic and can be used in different parallel or concurrent
applications. We will see quite a lot of this functional style being
used in the course for this reason, especially in the parallel and
distributed computing sections.
In [4]:
n = 10
xs = list(map(lambda x: x**2, range(n)))
xs
Out[4]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Python guidelines encourage use of named functions rather than lambdas¶
In [5]:
def square(x):
return x**2
xs = list(map(square, range(n)))
xs
Out[5]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Use vectorization¶
Traditionally, vectorization with numpy universal functions is the
way to write fast numerical programs in interpreted languages such as
Python. We see a lot of vectorized code in the course too.
In [6]:
import numpy as np
In [7]:
n = 10
xs = np.arange(n)**2
xs
Out[7]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
(2) Filling a list conditionally¶
Using a for loop¶
In [8]:
n = 10
xs = []
for i in range(n):
if i % 2 ==0:
xs.append(i**2)
xs
Out[8]:
[0, 4, 16, 36, 64]
Using a list comprehension¶
In [9]:
n = 10
xs = [i**2 for i in range(n) if i%2 == 0]
xs
Out[9]:
[0, 4, 16, 36, 64]
Using map¶
In [10]:
n = 10
xs = list(map(lambda x: x**2,
filter(lambda x: x%2==0, range(n))))
xs
Out[10]:
[0, 4, 16, 36, 64]
Python guidelines encourage use of named functions rather than lambdas¶
In [11]:
def square(x):
return x**2
def is_even(x):
return x%2 == 0
xs = list(map(square,
filter(is_even, range(n))))
xs
Out[11]:
[0, 4, 16, 36, 64]
Use vectorization¶
In [12]:
import numpy as np
In [13]:
n = 10
xs = np.arange(n)
xs = xs[xs % 2 == 0]
xs = xs**2
xs
Out[13]:
array([ 0, 4, 16, 36, 64])
(3) Writing as functions¶
In [14]:
def make_squares_for(n):
xs = []
for i in range(n):
xs.append(i**2)
return xs
In [15]:
make_squares_for(10)
Out[15]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
In [16]:
def make_squares_lc(n):
return [x**2 for x in range(n)]
In [17]:
make_squares_lc(10)
Out[17]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
In [18]:
def make_squares_map(n):
return list(map(square, range(n)))
In [19]:
make_squares_map(10)
Out[19]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
In [20]:
def make_squares_vec(n):
return np.arange(n)**2
In [21]:
make_squares_vec(10)
Out[21]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
(4) Timing¶
In [22]:
n = 1000000
%timeit make_squares_for(n)
%timeit make_squares_lc(n)
%timeit make_squares_map(n)
%timeit make_squares_vec(n)
1 loop, best of 3: 657 ms per loop
1 loop, best of 3: 611 ms per loop
1 loop, best of 3: 811 ms per loop
100 loops, best of 3: 9.82 ms per loop
(5) Compilation¶
In [23]:
from numba import njit
In [24]:
make_squares_for_numba = njit()(make_squares_for)
make_squares_for_numba(10)
Out[24]:
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
In [25]:
make_squares_vec_numba = njit()(make_squares_vec)
make_squares_vec_numba(10)
Out[25]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
In [26]:
n = 1000000
%timeit make_squares_for_numba(n)
%timeit make_squares_vec_numba(n)
10 loops, best of 3: 103 ms per loop
100 loops, best of 3: 10 ms per loop
Here we see the benefits to pre-allocating storage.
In [27]:
@njit
def make_squares_for_numba_prealloc(n):
xs = np.empty(n, dtype=np.int64)
for i in range(n):
xs[i] = i**2
return xs
In [28]:
make_squares_for_numba_prealloc(10)
Out[28]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
In [29]:
n = 1000000
%timeit make_squares_for_numba(n)
%timeit make_squares_for_numba_prealloc(n)
10 loops, best of 3: 104 ms per loop
100 loops, best of 3: 2.66 ms per loop
(6) Vectorizing scalar functions¶
In [30]:
@np.vectorize
def square_numpy(x):
return x**2
In [31]:
square_numpy(range(10))
Out[31]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
In [32]:
from numba import vectorize
In [33]:
@vectorize('int64(int64)')
def square_numba(x):
return x**2
In [34]:
square_numba(range(10))
Out[34]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
In [35]:
n = 1000000
%timeit square_numpy(np.arange(n))
%timeit square_numba(np.arange(n))
1 loop, best of 3: 902 ms per loop
100 loops, best of 3: 12.3 ms per loop
(7) With numba and JIT compilation, we need to reconsider the old taboo against looping.¶
In [36]:
def cabs2(z):
return z.real**2 + z.imag**2
def f(z, c, max_iter):
for i in range(max_iter):
z = z*z + c
if cabs2(z) > 4:
return i
return i
def julia(xs, ys, c, max_iter= 1000):
grid = np.empty((len(ys), len(xs)))
for a, x in enumerate(ys):
for b, y in enumerate(xs):
z = x + y*1.0j
grid[a, b] = f(z, c, max_iter)
return grid
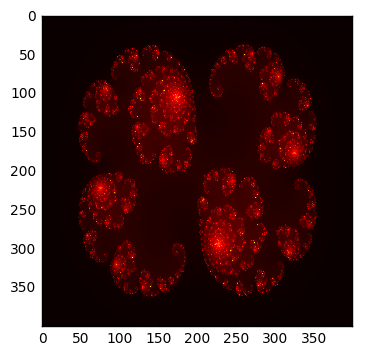
In [37]:
c = 0.285+0.01j
xs = np.linspace(-1.4, 1.4, 400)
ys = np.linspace(-1, 1, 400)
%time grid = julia(xs, ys, c)
plt.imshow(grid, cmap='hot', interpolation='nearest')
pass
CPU times: user 8.01 s, sys: 13.9 ms, total: 8.03 s
Wall time: 8.02 s
In [38]:
@njit
def cabs2(z):
return z.real**2 + z.imag**2
@njit
def f(z, c, max_iter):
for i in range(max_iter):
z = z*z + c
if cabs2(z) > 4:
return i
return i
@njit
def julia(xs, ys, c, max_iter= 1000):
grid = np.empty((len(ys), len(xs)))
for a, x in enumerate(ys):
for b, y in enumerate(xs):
z = x + y*1.0j
grid[a, b] = f(z, c, max_iter)
return grid
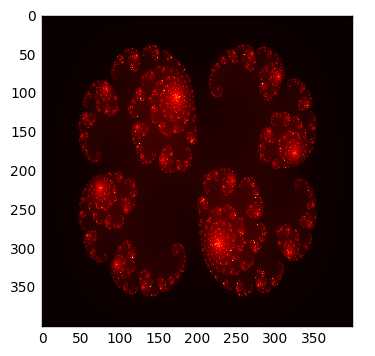
In [39]:
c = 0.285+0.01j
xs = np.linspace(-1.4, 1.4, 400)
ys = np.linspace(-1, 1, 400)
%time grid = julia(xs, ys, c)
plt.imshow(grid, cmap='hot', interpolation='nearest')
pass
CPU times: user 310 ms, sys: 5.7 ms, total: 315 ms
Wall time: 313 ms