Machine Learning with `sklearn`¶

This is mostly a tutorial to illustrate how to use scikit-learn to perform common machine learning pipelines. It is NOT meant to show how to do machine learning tasks well - you should take a machine learning course for that.

In [1]:

%matplotlib inline
import itertools as it
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import matplotlib.pyplot as plt

Resources¶

Official scikit-learn documentation

Example¶

We will try to separate rocks from mines using this [data set](https://archive.ics.uci.edu/ml/datasets/Connectionist+Bench+(Sonar,+Mines+vs.+Rocks).

From the description provided:

Data Set Information:

The file "sonar.mines" contains 111 patterns obtained by bouncing sonar signals off a metal cylinder at various angles and under various conditions. The file "sonar.rocks" contains 97 patterns obtained from rocks under similar conditions. The transmitted sonar signal is a frequency-modulated chirp, rising in frequency. The data set contains signals obtained from a variety of different aspect angles, spanning 90 degrees for the cylinder and 180 degrees for the rock.

Each pattern is a set of 60 numbers in the range 0.0 to 1.0. Each number represents the energy within a particular frequency band, integrated over a certain period of time. The integration aperture for higher frequencies occur later in time, since these frequencies are transmitted later during the chirp.

The label associated with each record contains the letter "R" if the object is a rock and "M" if it is a mine (metal cylinder). The numbers in the labels are in increasing order of aspect angle, but they do not encode the angle directly.

In [2]:

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-data', header=None, prefix='X')

In [3]:

df.shape

Out[3]:

(208, 61)

The last column are labels - make it a category¶

In [4]:

df.rename(columns={'X60':'Label'}, inplace=True)
df.Label = df.Label.astype('category')

In [5]:

df.head()

Out[5]:

	X0	X1	X2	X3	X4	X5	X6	X7	X8	X9	...	X51	X52	X53	X54	X55	X56	X57	X58	X59	Label
0	0.0200	0.0371	0.0428	0.0207	0.0954	0.0986	0.1539	0.1601	0.3109	0.2111	...	0.0027	0.0065	0.0159	0.0072	0.0167	0.0180	0.0084	0.0090	0.0032	R
1	0.0453	0.0523	0.0843	0.0689	0.1183	0.2583	0.2156	0.3481	0.3337	0.2872	...	0.0084	0.0089	0.0048	0.0094	0.0191	0.0140	0.0049	0.0052	0.0044	R
2	0.0262	0.0582	0.1099	0.1083	0.0974	0.2280	0.2431	0.3771	0.5598	0.6194	...	0.0232	0.0166	0.0095	0.0180	0.0244	0.0316	0.0164	0.0095	0.0078	R
3	0.0100	0.0171	0.0623	0.0205	0.0205	0.0368	0.1098	0.1276	0.0598	0.1264	...	0.0121	0.0036	0.0150	0.0085	0.0073	0.0050	0.0044	0.0040	0.0117	R
4	0.0762	0.0666	0.0481	0.0394	0.0590	0.0649	0.1209	0.2467	0.3564	0.4459	...	0.0031	0.0054	0.0105	0.0110	0.0015	0.0072	0.0048	0.0107	0.0094	R

5 rows × 61 columns

Exploratory data analysis¶

We can use simple plots to get some idea of what the data looks like

Is the separation between rocks and mines obvious?
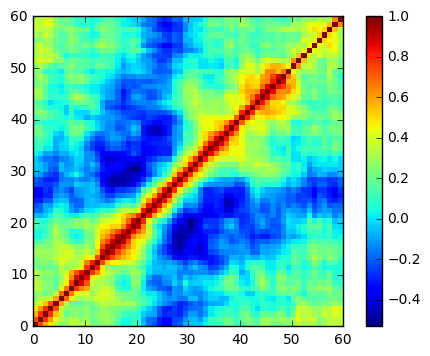
How correlated are the variables?
Do we need to standardize?
Are there outliers?

In [6]:

from pandas.tools.plotting import andrews_curves, parallel_coordinates

In [7]:

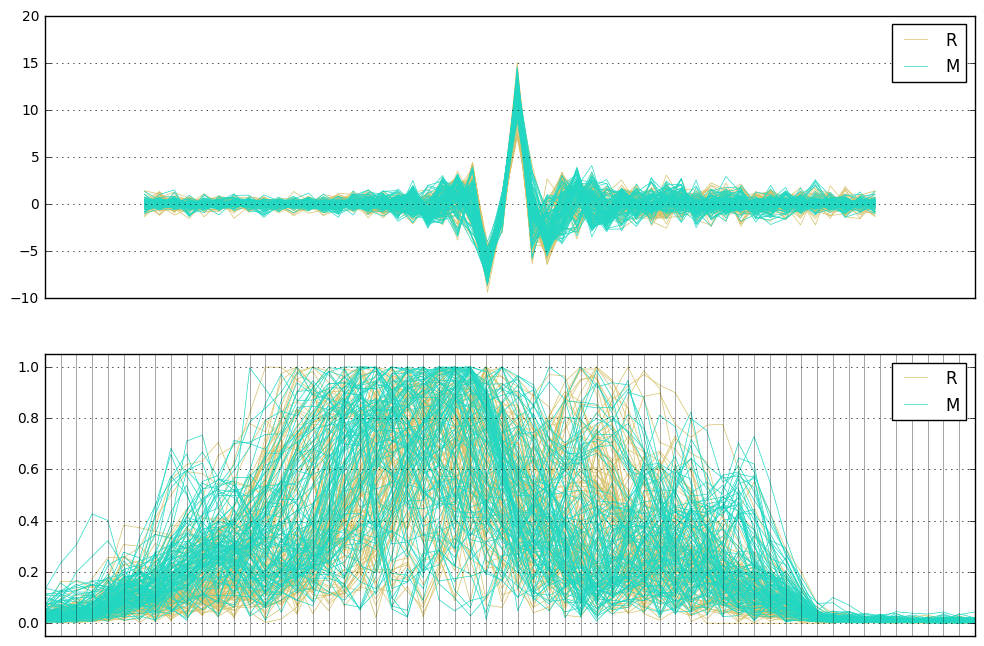
fig, axes = plt.subplots(2,1,figsize=(12,8))
andrews_curves(df, 'Label', samples=50, linewidth=0.5, ax=axes[0])
axes[0].set_xticks([])
parallel_coordinates(df, 'Label', linewidth=0.5, ax=axes[1],
                     axvlines_kwds={'linewidth': 0.5, 'color': 'black', 'alpha':0.5})
axes[1].set_xticks([])
axes[1].margins(0.05)
pass

../_images/notebooks_S06B_Machine_Learning_12_0.png

In [8]:

from sklearn.manifold import MDS

In [9]:

mds = MDS(n_components=2)

In [10]:

mds_data = mds.fit_transform(df.ix[:, :-1])

In [11]:

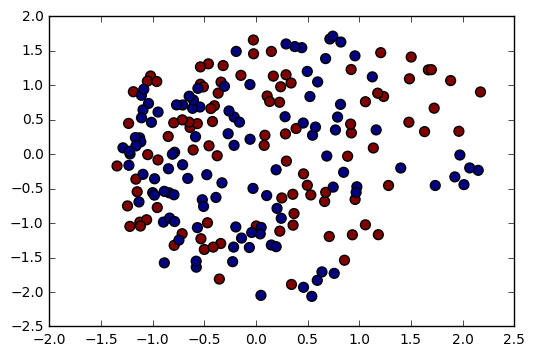
plt.scatter(mds_data[:, 0], mds_data[:, 1], c=df.Label.cat.codes, s=50);

../_images/notebooks_S06B_Machine_Learning_17_0.png

In [12]:

heatmap = plt.pcolor(df.corr(), cmap='jet')
plt.colorbar(heatmap)
plt.gca().set_aspect('equal')

../_images/notebooks_S06B_Machine_Learning_19_0.png

In [13]:

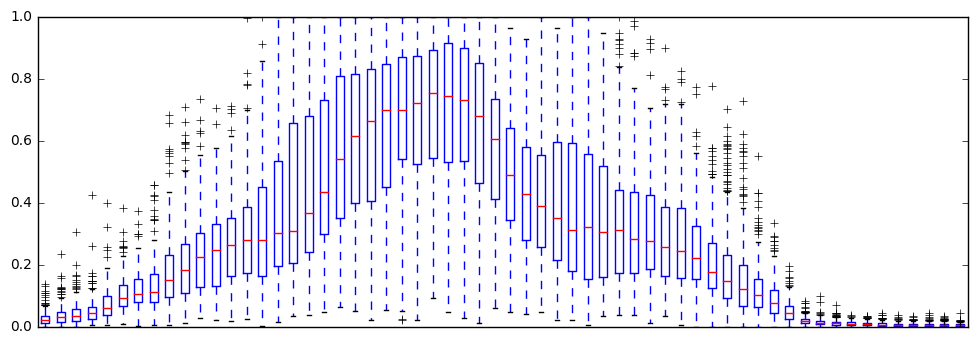
df.plot.box(figsize=(12,4), xticks=[])
pass

../_images/notebooks_S06B_Machine_Learning_21_0.png

In [14]:

df.plot.density(figsize=(6, 60), subplots=True, yticks=[])
pass

../_images/notebooks_S06B_Machine_Learning_23_0.png

Preprocessing¶

Box plots suggest we should standardize the data¶

In [15]:

from sklearn.preprocessing import StandardScaler, RobustScaler

In [16]:

data, labels = df.ix[:, :-1], df.ix[:, -1]

In [17]:

data.head(3)

Out[17]:

	X0	X1	X2	X3	X4	X5	X6	X7	X8	X9	...	X50	X51	X52	X53	X54	X55	X56	X57	X58	X59
0	0.0200	0.0371	0.0428	0.0207	0.0954	0.0986	0.1539	0.1601	0.3109	0.2111	...	0.0232	0.0027	0.0065	0.0159	0.0072	0.0167	0.0180	0.0084	0.0090	0.0032
1	0.0453	0.0523	0.0843	0.0689	0.1183	0.2583	0.2156	0.3481	0.3337	0.2872	...	0.0125	0.0084	0.0089	0.0048	0.0094	0.0191	0.0140	0.0049	0.0052	0.0044
2	0.0262	0.0582	0.1099	0.1083	0.0974	0.2280	0.2431	0.3771	0.5598	0.6194	...	0.0033	0.0232	0.0166	0.0095	0.0180	0.0244	0.0316	0.0164	0.0095	0.0078

3 rows × 60 columns

In [18]:

data_scaled = DataFrame(StandardScaler().fit_transform(data), columns=data.columns)

In [19]:

data_scaled.head(3)

Out[19]:

	X0	X1	X2	X3	X4	X5	X6	X7	X8	X9	...	X50	X51	X52	X53	X54	X55	X56	X57	X58	X59
0	-0.399551	-0.040648	-0.026926	-0.715105	0.364456	-0.101253	0.521638	0.297843	1.125272	0.021186	...	0.595283	-1.115432	-0.597604	0.680897	-0.295646	1.481635	1.763784	0.069870	0.171678	-0.658947
1	0.703538	0.421630	1.055618	0.323330	0.777676	2.607217	1.522625	2.510982	1.318325	0.588706	...	-0.297902	-0.522349	-0.256857	-0.843151	0.015503	1.901046	1.070732	-0.472406	-0.444554	-0.419852
2	-0.129229	0.601067	1.723404	1.172176	0.400545	2.093337	1.968770	2.852370	3.232767	3.066105	...	-1.065875	1.017585	0.836373	-0.197833	1.231812	2.827246	4.120162	1.309360	0.252761	0.257582

3 rows × 60 columns

If there are gross outliers, we can use a robust routine¶

In [20]:

data_robust = DataFrame(RobustScaler().fit_transform(data), columns=data.columns)

In [21]:

data_robust.head(3)

Out[21]:

	X0	X1	X2	X3	X4	X5	X6	X7	X8	X9	...	X50	X51	X52	X53	X54	X55	X56	X57	X58	X59
0	-0.126126	0.200000	0.217949	-0.581931	0.528726	0.096125	0.642271	0.538267	1.163123	0.182309	...	0.750000	-0.920635	-0.310433	0.723288	-0.037736	1.595142	1.791822	0.385185	0.390977	-0.387097
1	1.013514	0.682540	1.282051	0.619315	0.896746	2.476155	1.486320	2.646482	1.330279	0.665714	...	-0.112903	-0.317460	-0.066158	-0.493151	0.238994	1.983806	1.197026	-0.133333	-0.180451	-0.165899
2	0.153153	0.869841	1.938462	1.601246	0.560868	2.024590	1.862517	2.971685	2.987903	2.775925	...	-0.854839	1.248677	0.717557	0.021918	1.320755	2.842105	3.814126	1.570370	0.466165	0.460829

3 rows × 60 columns

Dimension reduction¶

In [22]:

from sklearn.decomposition import PCA

In [23]:

data.shape

Out[23]:

(208, 60)

In [24]:

pca = PCA()
data_scaled_pca = DataFrame(pca.fit_transform(data_scaled), columns=data.columns)

In [25]:

data_scaled.shape

Out[25]:

(208, 60)

In [26]:

v = pca.explained_variance_ratio_
vc = v.cumsum()
DataFrame(list(zip(it.count(), v, vc)), columns=['pc', 'explained', 'cumsum']).head(10)

Out[26]:

	pc	explained	cumsum
0	0	0.203466	0.203466
1	1	0.188972	0.392438
2	2	0.085500	0.477938
3	3	0.056792	0.534730
4	4	0.050071	0.584800
5	5	0.040650	0.625450
6	6	0.032790	0.658240
7	7	0.030465	0.688705
8	8	0.025660	0.714364
9	9	0.024911	0.739275

Let’s just use the principal components that explain at least 95% of total variance¶

In [27]:

n_comps = 1 + np.argmax(vc > 0.95)
n_comps

Out[27]:

In [28]:

data_scaled_pca = data_scaled_pca.ix[:, :n_comps]
data_scaled_pca.shape

Out[28]:

(208, 30)

In [29]:

data_scaled_pca.head()

Out[29]:

	X0	X1	X2	X3	X4	X5	X6	X7	X8	X9	...	X20	X21	X22	X23	X24	X25	X26	X27	X28	X29
0	1.921168	-1.370893	-1.666476	0.837913	-1.057324	1.712504	1.785716	-1.581264	0.335418	-1.028065	...	-1.208238	0.723202	0.304876	0.120470	-0.458567	-0.021847	-1.089710	0.096606	0.168123	-0.753434
1	-0.480125	7.586388	-1.275734	3.859346	2.121112	-2.186818	-1.742764	1.517061	0.307933	-1.341882	...	-2.388110	0.021429	-0.145524	-0.246021	0.117770	0.704112	-0.052387	-0.240064	-0.178744	-0.554605
2	3.859228	6.439860	-0.030635	5.454599	1.552060	1.181619	-1.820138	-1.495929	-1.152459	-1.006030	...	-1.740823	-2.000942	-0.295682	1.931963	0.758036	-0.113901	0.964319	0.214707	0.527529	-0.033003
3	4.597419	-3.104089	-1.785344	-1.115908	-2.785528	-2.072673	2.084530	1.707289	0.452390	-1.117318	...	-0.685825	1.307367	-0.662918	1.142591	-0.352601	-0.491193	-0.061186	0.150725	1.389191	0.642030
4	-0.533868	1.849847	-0.860097	3.302076	2.808954	-0.783945	0.362657	0.812621	0.184578	-0.023594	...	0.503340	0.258970	0.253982	1.199262	-0.165722	-0.041342	-0.589311	-0.500720	-1.549835	-0.783667

5 rows × 30 columns

In [30]:

df_pca = pd.concat([data_scaled_pca, labels], axis=1)
df_pca.shape

Out[30]:

(208, 31)

Classification¶

In [31]:

from sklearn.model_selection import train_test_split

In [32]:

X_train, X_test, y_train, y_test = \
  train_test_split(data_scaled_pca, labels, test_size=0.33, random_state=42)

In [33]:

from sklearn.linear_model import LogisticRegression

In [34]:

lr = LogisticRegression()

In [35]:

lr.fit(X_train, y_train)

Out[35]:

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)

Accuracy score¶

In [36]:

lr.score(X_test, y_test)

Out[36]:

0.78260869565217395

Using Support Vector Classifier and Grid Search¶

In [37]:

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV

In [38]:

parameters = [{'kernel': ['rbf'], 'gamma': [1e-3, 1e-4],
               'C': [1, 10, 100, 1000]},
               {'kernel': ['linear'], 'C': [1, 10, 100, 1000]}]

Do grid search with parallel jobs¶

In [39]:

clf = GridSearchCV(SVC(C=1), parameters, cv=5, scoring='accuracy', n_jobs=-1)
clf.fit(X_train, y_train.codes)
pass

In [40]:

clf.best_params_

Out[40]:

{'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}

In [41]:

clf.best_score_

Out[41]:

0.76978417266187049

In [42]:

clf.score(X_test, y_test.codes)

Out[42]:

0.88405797101449279

In [43]:

from sklearn.metrics import classification_report

In [44]:

y_true, y_pred = y_test.codes, clf.predict(X_test)
print(classification_report(y_true, y_pred))

             precision    recall  f1-score   support

          0       0.88      0.92      0.90        38
          1       0.90      0.84      0.87        31

avg / total       0.88      0.88      0.88        69

Using a Random Forests Classifier¶

In [45]:

from sklearn.ensemble import RandomForestClassifier

In [46]:

X_train, X_test, y_train, y_test = \
  train_test_split(data_scaled, labels, test_size=0.33, random_state=42)

In [47]:

parameters = [{'n_estimators': list(range(25, 201, 25)),
               'max_features': list(range(2, 15, 2))}]
clf = GridSearchCV(RandomForestClassifier(), parameters,
                   cv=5, scoring='accuracy', n_jobs=-1)
clf.fit(X_train, y_train.codes)
pass

In [48]:

clf.best_params_

Out[48]:

{'max_features': 6, 'n_estimators': 150}

In [49]:

clf.score(X_test, y_test.codes)

Out[49]:

0.85507246376811596

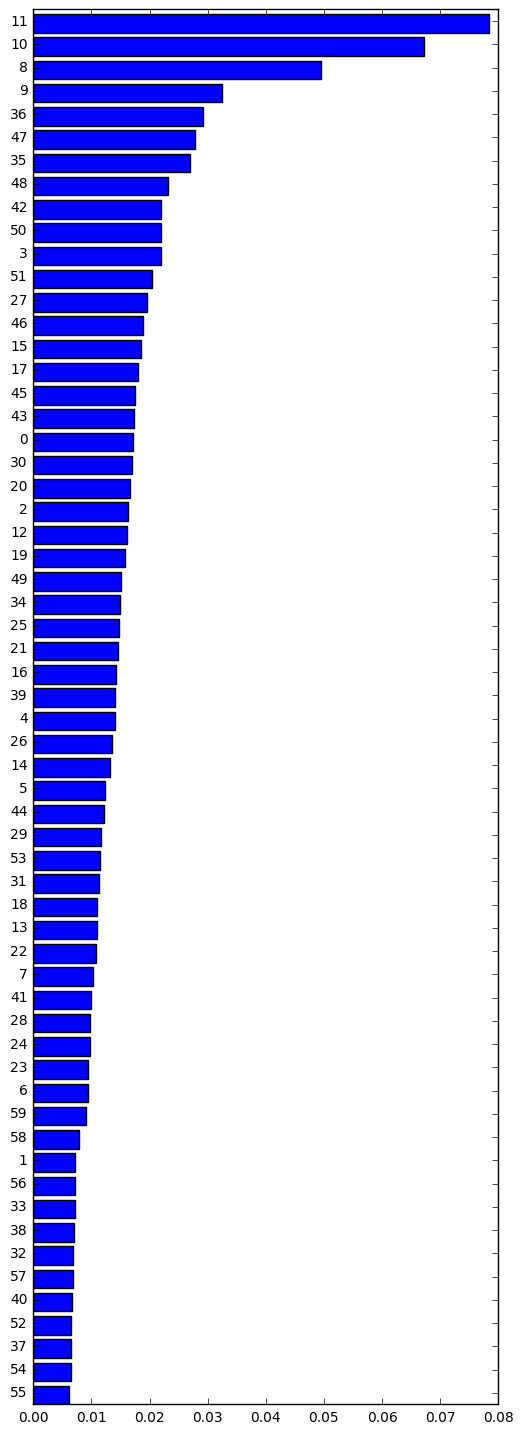
Which features are important?¶

In [50]:

imp = clf.best_estimator_.feature_importances_
idx = np.argsort(imp)

In [51]:

plt.figure(figsize=(6, 18))
plt.barh(range(len(imp)), imp[idx])
plt.yticks(np.arange(len(imp))+0.5, idx)
pass

../_images/notebooks_S06B_Machine_Learning_73_0.png

Using a Pipeline¶

For cross-validation (e.g. grid search for best parameters), we often need to chain a series of steps and treat it as a single model. This chaining can be done with a Pipeline object.

In [52]:

from sklearn.pipeline import Pipeline

In [53]:

X_train, X_test, y_train, y_test = \
  train_test_split(data_scaled, labels, test_size=0.33, random_state=42)

In [54]:

scaler = StandardScaler()
pca = PCA()
clf = LogisticRegression()

pipe = Pipeline(steps=[('scaler', scaler), ('pca', pca), ('clf', clf)])
n_components = [20, 30, 40, 50, 60]
Cs = np.logspace(-4, 4, 1)

estimator = GridSearchCV(pipe,
                         dict(pca__n_components=n_components,
                         clf__C=Cs), n_jobs=-1)
estimator.fit(X_train, y_train.codes)
pass

In [55]:

estimator.best_estimator_.named_steps['pca'].n_components

Out[55]:

In [56]:

estimator.score(X_test, y_test.codes)

Out[56]:

0.76811594202898548

In [57]:

y_true, y_pred = y_test.codes, estimator.predict(X_test)
print(classification_report(y_true, y_pred))

             precision    recall  f1-score   support

          0       0.84      0.71      0.77        38
          1       0.70      0.84      0.76        31

avg / total       0.78      0.77      0.77        69

Machine Learning with sklearn¶

Resources¶

Example¶

The last column are labels - make it a category¶

Exploratory data analysis¶

Preprocessing¶

Box plots suggest we should standardize the data¶

If there are gross outliers, we can use a robust routine¶

Dimension reduction¶

Let’s just use the principal components that explain at least 95% of total variance¶

Classification¶

Accuracy score¶

Using Support Vector Classifier and Grid Search¶

Do grid search with parallel jobs¶

Using a Random Forests Classifier¶

Which features are important?¶

Using a Pipeline¶

Machine Learning with `sklearn`¶