Constrained Optimization¶
In [19]:
import numpy as np
from scipy.linalg import cholesky, solve_triangular, cho_solve, cho_factor
from scipy.linalg import solve
from scipy.optimize import minimize
Lagrange multipliers and constrained optimization¶
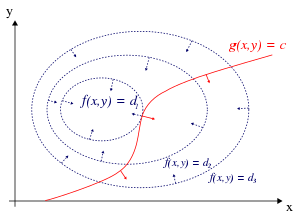
Recall why Lagrange multipliers are useful for constrained optimization - a stationary point must be where the constraint surface \(g\) touches a level set of the function \(f\) (since the value of \(f\) does not change on a level set). At that point, \(f\) and \(g\) are parallel, and hence their gradients are also parallel (since the gradient is normal to the level set). So we want to solve
or equivalently,
Lagrange multipliers
Example 1¶
Maximize \(f (x, y, z) = xy + yz\) subject to the constraints \(x + 2y = 6\) and \(x − 3z = 0\).
We set up the equations
Now set partial derivatives to zero and solve the following set of equations
which is a linear equation in \(x, y, z, \lambda, \mu\)
In [5]:
A = np.array([
[0, 1, 0, -1, -1],
[1, 0, 1, -2, 0],
[0, 1, 0, 0, 3],
[1, 2, 0, 0, 0],
[1, 0,-3, 0, 0]])
b = np.array([0,0,0,6,0])
sol = solve(A, b)
In [6]:
sol
Out[6]:
array([ 3. , 1.5, 1. , 2. , -0.5])
In [12]:
def f(x, y, z):
return x*y + y*z
In [14]:
f(*sol[:3])
Out[14]:
6.0
Using scipy.optimize¶
We first need to set this as a minimization problem.
In [15]:
def f(x):
return -(x[0]*x[1] + x[1]*x[2])
In [16]:
cons = ({'type': 'eq',
'fun' : lambda x: np.array([x[0] + 2*x[1] - 6, x[0] - 3*x[2]])})
In [23]:
x0 = np.array([2,2,0.67])
res = minimize(f, x0, constraints=cons)
Out[23]:
array([2.99999979, 1.50000011, 0.99999993])
In [25]:
res.fun
Out[25]:
-5.999999999999969
In [26]:
res.x
Out[26]:
array([2.99999979, 1.50000011, 0.99999993])
Example 2¶
Find the minimum of the following quadratic function on \(\mathbb{R}^2\)
Under the constraints:
- Use a matrix decomposition method to find the minimum of the
unconstrained problem without using
scipy.optimize(Use library functions - no need to code your own). Note: for full credit you should exploit matrix structure. - Find the solution using constrained optimization with the
scipy.optimizepackage. - Use Lagrange multipliers and solving the resulting set of equations
directly without using
scipy.optimize.
Solve unconstrained problem¶
To find the minimum, we differentiate \(f(x)\) with respect to \(x^T\) and set it equal to \(0\). We thus need to solve
or
We see that \(A\) is a symmetric positive definite real matrix. Hence we use Cholesky factorization.
Steps
In [3]:
A = np.array([
[13,5],
[5,7]
])
b = np.array([1,1]).reshape(-1,1)
c = 2
In [4]:
L = cholesky(A, lower=True)
y = solve_triangular(L, -b/2, lower=True)
x = solve_triangular(L.T, y, lower=False)
In [5]:
x
Out[5]:
array([[-0.01515152],
[-0.06060606]])
In [6]:
cho_solve(cho_factor(A), -b/2)
Out[6]:
array([[-0.01515152],
[-0.06060606]])
Solve constrained problem using scipy.optimize¶
In [7]:
f = lambda x, A, b, c: x.T @ A @ x + b.T @ x + c
In [8]:
from scipy.optimize import minimize
In [9]:
cons = ({'type': 'eq', 'fun': lambda x: 2*x[0] - 5*x[1] - 2},
{'type': 'eq', 'fun': lambda x: x[0] + x[1] - 1})
res = minimize(f, [0,0], constraints=cons, args=(A, b, c))
res.x
Out[9]:
array([1.00000000e+00, 3.41607086e-16])
Solve constrained problem using Lagrange multipliers¶
We set up the equations
Sometimes this is written as
All this means is a final sign change in the estimated values of \(\lambda\) and \(\mu\).
We show the original equations for convenience
where
Under the constraints:
To make the calculations explicit, we rewrite \(F\) as
Taking partial derivatives, we get
Plugging in the numbers and expressing in matrix form, we get
With a bit of practice, you can probably just write the matrix directly by inspection.
In [11]:
A = np.array([
[26, 10, 2, 1],
[10, 14, -5, 1],
[2, -5, 0, 0],
[1, 1, 0, 0]
])
b = np.array([-1, -1, 2, 1]).reshape(-1,1)
In [12]:
solve(A, b)
Out[12]:
array([[ 1.00000000e+00],
[-4.37360585e-17],
[-2.28571429e+00],
[-2.24285714e+01]])