Vectors¶
Informally, we think of a vector as an object that has magnitude and direction. More formally, we think of an \(n\)-dimensional vector as an ordered tuple of numbers \((x_1, x_2, \ldots, x_n)\) that follows the rules of scalar multiplication and vector addition.
In [1]:
%matplotlib inline
In [2]:
import numpy as np
import matplotlib.pyplot as plt
Vector space¶
A vector space is a collection of vectors which is closed under addition and scalar multiplication.
Examples:
- Euclidean plane \(\mathbb{R}^2\) is a familiar vector space
- The vector \(\pmatrix{0 & 0}\) is a trivial vector space that is a vector subspace of Euclidean space.
- Polynomial functions of order \(k\) is a vector space
Polynomials of order 3 have the form \(ax^3 + bx^2 + cx + d\), and can be represented as the vector
- The space of all continuous functions is a vector space
Consider two continuous functions, say, \(f(x) = x^2\) and \(g(x) = x^3)\). Scalar multiplication \((2 f)(x) = 2x^2\) and addition \((f + g)(x) = x^2 + x^3\) are well defined and the result is a continuous function, so the space of all continuous functions is also a vector space. In this case, it is an infinite-dimensional vector space.
Vector spaces are important because the theorems of linear algebra apply to all vector spaces, not just Euclidean space.
Column vectors¶
When we describe a vector \(x\), we mean the column vector. The row vector is denoted \(x^T\).
In [3]:
x = np.random.random((5,1))
x
Out[3]:
array([[0.17177801],
[0.21054051],
[0.21676041],
[0.73357656],
[0.36831598]])
In [4]:
x.T
Out[4]:
array([[0.17177801, 0.21054051, 0.21676041, 0.73357656, 0.36831598]])
Length¶
The length of a vector is the Euclidean norm (i.e. Pythagoras theorem)
In [6]:
np.linalg.norm(x)
Out[6]:
0.8914097289661268
In [7]:
np.sqrt(np.sum(x**2))
Out[7]:
0.8914097289661268
Direction¶
In [8]:
n = x/np.linalg.norm(x)
n
Out[8]:
array([[0.19270377],
[0.23618826],
[0.24316585],
[0.82293982],
[0.41318371]])
In [9]:
np.linalg.norm(n)
Out[9]:
1.0
Norms and distances¶
Recall that the ‘norm’ of a vector \(v\), denoted \(||v||\) is simply its length. For a vector with components
The distance between two vectors is the length of their difference:
In [10]:
u = np.array([3,0]).reshape((-1,1))
v = np.array([0,4]).reshape((-1,1))
In [11]:
np.linalg.norm(u - v)
Out[11]:
5.0
In [12]:
np.linalg.norm(v - u)
Out[12]:
5.0
In [13]:
np.sqrt(np.sum((u - v)**2))
Out[13]:
5.0
Vector operations¶
In [14]:
x = np.arange(3).reshape((-1,1))
y = np.arange(3).reshape((-1,1))
In [15]:
3 * x
Out[15]:
array([[0],
[3],
[6]])
In [16]:
x + y
Out[16]:
array([[0],
[2],
[4]])
In [17]:
3*x + 4*y
Out[17]:
array([[ 0],
[ 7],
[14]])
In [18]:
x.T
Out[18]:
array([[0, 1, 2]])
Dot product¶
The dot product of two vectors \(u\) and \(v\) is written as \(u \cdot v\) and its value is given by \(u^Tv\). The dot product of two \(n\) dimensional vectors \(v\) and \(w\) is given by:
I.e. the dot product is just the sum of the product of the components.
The inner product \(\langle u,v \rangle\) of two vectors is a generalization of the dot product. It is any function that takes two vectors, returns a scalar (here we just consider inner products that return real numbers), and obeys the following properties:
- symmetry \(\langle u,v \rangle = \langle v,u \rangle\)
- positive definite
- \(\langle v,v \rangle \ge 0\)
- \(\langle v,v \rangle = 0 \implies v = 0\)
- bilinear
- \(\langle au,v \rangle = a \langle u,v \rangle\)
- \(\langle u + v,w \rangle = \langle u,w \rangle + \langle v,w \rangle\)
- Linearity also applies to second argument because of symmetry
Any inner product determines a norm via:
In [19]:
u = np.array([3,3]).reshape((-1,1))
v = np.array([2,0]).reshape((-1,1))
In [20]:
np.dot(u.T, v)
Out[20]:
array([[6]])
You can also use the @ operator to do matrix multiplication
In [21]:
u.T @ v
Out[21]:
array([[6]])
In [22]:
np.sum(u * v)
Out[22]:
6
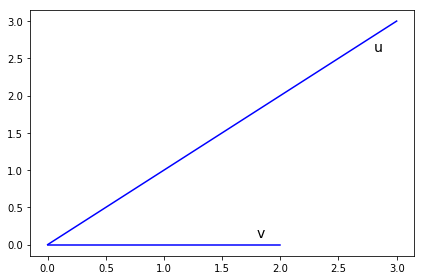
Geometrically, the dot product is the product of the length of \(v\) and the length of the projection of \(u\) onto the unit vector \(\widehat{v}\).
In [23]:
plt.plot(*zip(np.zeros_like(u), u), 'b-')
plt.text(1.8, 0.1, 'v', fontsize=14)
plt.plot(*zip(np.zeros_like(v), v), 'b-')
plt.text(2.8, 2.6, 'u', fontsize=14)
plt.tight_layout()
pass
In [24]:
cos_angle = np.dot(u.T, v)/(np.linalg.norm(u)*np.linalg.norm(v))
In [25]:
cos_angle
Out[25]:
array([[0.70710678]])
In [26]:
theta = 180/np.pi*np.arccos(cos_angle)
In [27]:
theta
Out[27]:
array([[45.]])
Outer product¶
Note that the inner product is just matrix multiplication of a \(1\times n\) vector with an \(n\times 1\) vector. In fact, we may write:
The outer product of two vectors is just the opposite. It is given by:
Note that I am considering \(v\) and \(w\) as column vectors. The result of the inner product is a scalar. The result of the outer product is a matrix.
For example, if \(v\) and \(w\) are both in \(\mathbb{R}^3\)
In [28]:
v = np.array([1,2,3]).reshape((-1,1))
In [29]:
v
Out[29]:
array([[1],
[2],
[3]])
In [30]:
v @ v.T
Out[30]:
array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]])
In [31]:
np.outer(v, v)
Out[31]:
array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]])