Numbers¶
In [1]:
%matplotlib inline
In [2]:
import matplotlib.pyplot as plt
In [3]:
import numpy as np
The ndarray: Vectors, matrices and tenosrs¶
dtype, shape, strides
Vector¶
In [4]:
x = np.array([1,2,3])
x
Out[4]:
array([1, 2, 3])
In [5]:
type(x)
Out[5]:
numpy.ndarray
In [6]:
x.dtype
Out[6]:
dtype('int64')
In [7]:
x.shape
Out[7]:
(3,)
In [8]:
x.strides
Out[8]:
(8,)
Matrix¶
In [9]:
x = np.array([[1,2,3], [4,5,6]], dtype=np.int32)
x
Out[9]:
array([[1, 2, 3],
[4, 5, 6]], dtype=int32)
In [10]:
x.dtype
Out[10]:
dtype('int32')
In [11]:
x.shape
Out[11]:
(2, 3)
In [12]:
x.strides
Out[12]:
(12, 4)
Tensor¶
In [13]:
x = np.arange(24).reshape((2,3,4))
In [14]:
x
Out[14]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
Creating ndarrays¶
From a file¶
In [15]:
%%file numbers.txt
a,b,c # can also skip headers
1,2,3
4,5,6
Overwriting numbers.txt
In [16]:
np.loadtxt('numbers.txt', dtype='int', delimiter=',',
skiprows=1, comments='#')
Out[16]:
array([[1, 2, 3],
[4, 5, 6]])
From Python lists or tuples¶
In [17]:
np.array([
[1,2,3],
[4,5,6]
])
Out[17]:
array([[1, 2, 3],
[4, 5, 6]])
From ranges¶
arange, linspace, logspace
In [18]:
np.arange(1, 7).reshape((2,3))
Out[18]:
array([[1, 2, 3],
[4, 5, 6]])
In [19]:
np.linspace(1, 10, 4)
Out[19]:
array([ 1., 4., 7., 10.])
In [20]:
np.logspace(0, 4, 5, dtype='int')
Out[20]:
array([ 1, 10, 100, 1000, 10000])
From a function¶
fromfunciton
In [21]:
np.fromfunction(lambda i, j: i*3 + j + 1, (2,3))
Out[21]:
array([[ 1., 2., 3.],
[ 4., 5., 6.]])
In [22]:
np.fromfunction(lambda i, j: (i-2)**2 + (j-2)**2, (5,5))
Out[22]:
array([[ 8., 5., 4., 5., 8.],
[ 5., 2., 1., 2., 5.],
[ 4., 1., 0., 1., 4.],
[ 5., 2., 1., 2., 5.],
[ 8., 5., 4., 5., 8.]])
In [23]:
np.fromfunction(lambda i, j: np.where(i<j, 1, np.where(i==j,0, -1)), (5,5))
Out[23]:
array([[ 0, 1, 1, 1, 1],
[-1, 0, 1, 1, 1],
[-1, -1, 0, 1, 1],
[-1, -1, -1, 0, 1],
[-1, -1, -1, -1, 0]])
Adapted from Circle Squared
In [24]:
xs = np.fromfunction(lambda i, j: 0.27**2*(i**2 + j**2) % 1.5,
(400, 400),)
plt.figure(figsize=(8,8))
plt.imshow(xs, interpolation='nearest', cmap=plt.cm.YlOrBr)
plt.xticks([])
plt.yticks([])
pass

From special construcotrs¶
zeoros, ones, eye
In [25]:
np.zeros((2,3))
Out[25]:
array([[ 0., 0., 0.],
[ 0., 0., 0.]])
In [26]:
np.ones((2,3))
Out[26]:
array([[ 1., 1., 1.],
[ 1., 1., 1.]])
In [27]:
np.eye(3)
Out[27]:
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
In [28]:
np.eye(3, 4)
Out[28]:
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.]])
In [29]:
np.eye(4, k=-1)
Out[29]:
array([[ 0., 0., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.]])
From random variables¶
Convenience functions¶
rand, randn
In [30]:
np.random.rand(2,3)
Out[30]:
array([[ 0.04737547, 0.82228651, 0.22224204],
[ 0.96886745, 0.54149529, 0.94853004]])
In [31]:
np.random.randn(2,3)
Out[31]:
array([[-0.80516331, 0.9086527 , -1.21134755],
[-0.08444392, 1.00515737, 0.94762797]])
Distributions¶
uniform, normal, randint, poisson, multinomial, multivariate_ normal
In [32]:
np.random.uniform(0, 1, (2,3))
Out[32]:
array([[ 0.12880127, 0.32643222, 0.52082391],
[ 0.35404701, 0.54964578, 0.456206 ]])
In [33]:
np.random.normal(0, 1, (2,3))
Out[33]:
array([[ 0.8195548 , 0.43940477, -0.24901744],
[ 2.6248388 , 0.16150201, 0.12905971]])
In [34]:
np.random.randint(0, 10, (4,5))
Out[34]:
array([[5, 0, 2, 3, 9],
[8, 5, 1, 1, 9],
[5, 5, 2, 0, 2],
[2, 0, 5, 7, 4]])
In [35]:
np.random.poisson(10, (4,5))
Out[35]:
array([[ 8, 9, 17, 8, 15],
[ 8, 9, 12, 12, 11],
[ 6, 8, 10, 13, 6],
[ 7, 12, 8, 16, 8]])
In [36]:
np.random.multinomial(n=5, pvals=np.ones(5)/5, size=8)
Out[36]:
array([[2, 0, 0, 2, 1],
[4, 0, 0, 1, 0],
[3, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 1, 2, 1, 1],
[1, 1, 2, 1, 0],
[2, 0, 1, 1, 1],
[0, 1, 1, 1, 2]])
In [37]:
np.random.multivariate_normal(mean=[10,20,30], cov=np.eye(3), size=4)
Out[37]:
array([[ 9.34907429, 20.28742704, 31.20954084],
[ 10.61473257, 19.60538925, 29.09199082],
[ 9.10517086, 19.82157961, 28.57954932],
[ 8.35947889, 22.60010629, 29.05471801]])
Indexing¶
In [38]:
x = np.arange(20).reshape((4,5))
x
Out[38]:
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
Using slices¶
In [41]:
x[1,:]
Out[41]:
array([5, 6, 7, 8, 9])
In [42]:
x[:,1]
Out[42]:
array([ 1, 6, 11, 16])
In [43]:
x[1:3,1:3]
Out[43]:
array([[ 6, 7],
[11, 12]])
Extrcting blocks with arbitrary row and column lists (fancy indexing)¶
np.ix_
In [45]:
x[:, [0,3]]
Out[45]:
array([[ 0, 3],
[ 5, 8],
[10, 13],
[15, 18]])
Warning: Fancy indexing can only be used for 1 dimension.
In [46]:
x[[0,2],[0,3]]
Out[46]:
array([ 0, 13])
Use the helper np.ix_ to extract arbitrary blocks.
In [47]:
x[np.ix_([0,2], [0,3])]
Out[47]:
array([[ 0, 3],
[10, 13]])
A slice is a view, not a copy¶
In [48]:
x
Out[48]:
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
In [49]:
y = x[1:-1, 1:-1]
y
Out[49]:
array([[ 6, 7, 8],
[11, 12, 13]])
In [50]:
y *= 10
In [51]:
y
Out[51]:
array([[ 60, 70, 80],
[110, 120, 130]])
In [52]:
x
Out[52]:
array([[ 0, 1, 2, 3, 4],
[ 5, 60, 70, 80, 9],
[ 10, 110, 120, 130, 14],
[ 15, 16, 17, 18, 19]])
Use the copy method to convert a view to a copy
In [53]:
z = x[1:-1, 1:-1].copy()
In [54]:
z
Out[54]:
array([[ 60, 70, 80],
[110, 120, 130]])
In [55]:
z[:] = 0
In [56]:
z
Out[56]:
array([[0, 0, 0],
[0, 0, 0]])
In [57]:
x
Out[57]:
array([[ 0, 1, 2, 3, 4],
[ 5, 60, 70, 80, 9],
[ 10, 110, 120, 130, 14],
[ 15, 16, 17, 18, 19]])
Boolean indexing¶
In [58]:
x[x % 2 == 0]
Out[58]:
array([ 0, 2, 4, 60, 70, 80, 10, 110, 120, 130, 14, 16, 18])
In [59]:
x [x > 3]
Out[59]:
array([ 4, 5, 60, 70, 80, 9, 10, 110, 120, 130, 14, 15, 16,
17, 18, 19])
Functions that return indexes¶
In [60]:
idx = np.nonzero(x)
idx
Out[60]:
(array([0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3]),
array([1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4]))
In [61]:
x[idx]
Out[61]:
array([ 1, 2, 3, 4, 5, 60, 70, 80, 9, 10, 110, 120, 130,
14, 15, 16, 17, 18, 19])
In [62]:
idx = np.where(x > 3)
idx
Out[62]:
(array([0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3]),
array([4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4]))
In [63]:
x[idx]
Out[63]:
array([ 4, 5, 60, 70, 80, 9, 10, 110, 120, 130, 14, 15, 16,
17, 18, 19])
Margins and the axis argument¶
In [64]:
x
Out[64]:
array([[ 0, 1, 2, 3, 4],
[ 5, 60, 70, 80, 9],
[ 10, 110, 120, 130, 14],
[ 15, 16, 17, 18, 19]])
The 0th axis has 4 items, the 1st axis has 5 items.
In [65]:
x.shape
Out[65]:
(4, 5)
In [66]:
x.mean()
Out[66]:
35.149999999999999
Marginalizing out the 0th axis = column summaries¶
In [67]:
x.mean(axis=0)
Out[67]:
array([ 7.5 , 46.75, 52.25, 57.75, 11.5 ])
Marginalizing out the 1st axis = row summaries¶
In [68]:
x.mean(axis=1)
Out[68]:
array([ 2. , 44.8, 76.8, 17. ])
Note marginalizing out the last axis is a common default.
In [69]:
x.mean(axis=-1)
Out[69]:
array([ 2. , 44.8, 76.8, 17. ])
Marginalization works for higher dimensions in the same way¶
In [70]:
x = np.random.random((2,3,4))
x
Out[70]:
array([[[ 0.25091919, 0.97511897, 0.6520031 , 0.56832053],
[ 0.97444408, 0.72376855, 0.15067567, 0.10752009],
[ 0.20627991, 0.0234196 , 0.70143528, 0.87408988]],
[[ 0.95505841, 0.79364654, 0.76668484, 0.47971008],
[ 0.34780788, 0.44169709, 0.63645331, 0.96215426],
[ 0.92889169, 0.52710155, 0.22280321, 0.04262088]]])
In [71]:
x.shape
Out[71]:
(2, 3, 4)
In [72]:
x.mean(axis=0).shape
Out[72]:
(3, 4)
In [73]:
x.mean(axis=1).shape
Out[73]:
(2, 4)
In [74]:
x.mean(axis=2).shape
Out[74]:
(2, 3)
In [75]:
x.mean(axis=(0,1)).shape
Out[75]:
(4,)
In [76]:
x.mean(axis=(0,2)).shape
Out[76]:
(3,)
In [77]:
x.mean(axis=(1,2)).shape
Out[77]:
(2,)
Broadcasting¶
In [78]:
x1 = np.arange(12)
In [79]:
x1
Out[79]:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
In [80]:
x1 * 10
Out[80]:
array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110])
In [81]:
x2 = np.random.randint(0,10,(3,4))
In [82]:
x2
Out[82]:
array([[3, 0, 1, 2],
[2, 4, 0, 7],
[9, 9, 3, 0]])
In [83]:
x2 * 10
Out[83]:
array([[30, 0, 10, 20],
[20, 40, 0, 70],
[90, 90, 30, 0]])
In [84]:
x2.shape
Out[84]:
(3, 4)
Column-wise broadcasting¶
In [85]:
mu = np.mean(x2, axis=0)
mu.shape
Out[85]:
(4,)
In [86]:
x2 - mu
Out[86]:
array([[-1.66666667, -4.33333333, -0.33333333, -1. ],
[-2.66666667, -0.33333333, -1.33333333, 4. ],
[ 4.33333333, 4.66666667, 1.66666667, -3. ]])
In [87]:
(x2 - mu).mean(axis=0)
Out[87]:
array([ -2.96059473e-16, 2.96059473e-16, 7.40148683e-17,
0.00000000e+00])
Row wise broadcasting¶
In [88]:
mu = np.mean(x2, axis=1)
mu.shape
Out[88]:
(3,)
In [89]:
try:
x2 - mu
except ValueError as e:
print(e)
operands could not be broadcast together with shapes (3,4) (3,)
We can add a “dummy” axis using None or np.newaxis¶
In [90]:
mu[:, None].shape
Out[90]:
(3, 1)
In [91]:
x2 - mu[:, None]
Out[91]:
array([[ 1.5 , -1.5 , -0.5 , 0.5 ],
[-1.25, 0.75, -3.25, 3.75],
[ 3.75, 3.75, -2.25, -5.25]])
In [92]:
x2 - mu[:, np.newaxis]
Out[92]:
array([[ 1.5 , -1.5 , -0.5 , 0.5 ],
[-1.25, 0.75, -3.25, 3.75],
[ 3.75, 3.75, -2.25, -5.25]])
In [93]:
np.mean(x2 - mu[:, None], axis=1)
Out[93]:
array([ 0., 0., 0.])
Reshaping works too¶
In [94]:
x2 - mu.reshape((-1,1))
Out[94]:
array([[ 1.5 , -1.5 , -0.5 , 0.5 ],
[-1.25, 0.75, -3.25, 3.75],
[ 3.75, 3.75, -2.25, -5.25]])
Broadcasting examples¶
Creating a 12 by 12 multiplication table
In [95]:
x = np.arange(1, 13)
x[:,None] * x[None,:]
Out[95]:
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24],
[ 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36],
[ 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48],
[ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60],
[ 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72],
[ 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84],
[ 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96],
[ 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108],
[ 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120],
[ 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132],
[ 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144]])
Scaling to have zero mean and unit standard devation for each feature.
In [96]:
x = np.random.normal(10, 5,(3,4))
x
Out[96]:
array([[ 7.65396872, 8.74106757, 7.26659687, 9.68096491],
[ 9.27132075, 7.89349589, 9.47813473, 7.04088855],
[ 13.78187972, 7.39243968, 10.90034325, 4.27477767]])
Standardize column-wise
In [97]:
(x - x.mean(axis=0))/x.std(axis=0)
Out[97]:
array([[-0.99566783, 1.31524702, -1.30321654, 1.21511731],
[-0.37192708, -0.20751913, 0.17598238, 0.01903327],
[ 1.36759491, -1.10772789, 1.12723416, -1.23415058]])
Standardize row-wise
In [98]:
(x - x.mean(axis=1)[:, None])/x.std(axis=1)[:, None]
Out[98]:
array([[-0.72037796, 0.42843253, -1.12973985, 1.42168528],
[ 0.84786879, -0.52591836, 1.0540767 , -1.37602714],
[ 1.31012381, -0.47301018, 0.50595856, -1.34307219]])
Combining ndarrays¶
In [99]:
x1 = np.zeros((3,4))
x2 = np.ones((3,5))
x3 = np.eye(4)
In [100]:
x1
Out[100]:
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]])
In [101]:
x2
Out[101]:
array([[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]])
In [102]:
x3
Out[102]:
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
Binding rows when number of columns is the same¶
In [103]:
np.r_[x1, x3]
Out[103]:
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
Binding columns when number of rows is the same¶
In [104]:
np.c_[x1, x2]
Out[104]:
array([[ 0., 0., 0., 0., 1., 1., 1., 1., 1.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1.]])
You can combine more than 2 at a time¶
In [105]:
np.c_[x1, x2, x1]
Out[105]:
array([[ 0., 0., 0., 0., 1., 1., 1., 1., 1., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1., 0., 0., 0., 0.]])
Stacking¶
In [106]:
np.vstack([x1, x3])
Out[106]:
array([[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
In [107]:
np.hstack([x1, x2])
Out[107]:
array([[ 0., 0., 0., 0., 1., 1., 1., 1., 1.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1.],
[ 0., 0., 0., 0., 1., 1., 1., 1., 1.]])
In [108]:
np.dstack([x2, 2*x2, 3*x2])
Out[108]:
array([[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]],
[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]],
[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]]])
Generic stack with axis argument¶
In [109]:
np.stack([x2, 2*x2, 3*x2], axis=0)
Out[109]:
array([[[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]],
[[ 2., 2., 2., 2., 2.],
[ 2., 2., 2., 2., 2.],
[ 2., 2., 2., 2., 2.]],
[[ 3., 3., 3., 3., 3.],
[ 3., 3., 3., 3., 3.],
[ 3., 3., 3., 3., 3.]]])
In [110]:
np.stack([x2, 2*x2, 3*x2], axis=1)
Out[110]:
array([[[ 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3.]],
[[ 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3.]],
[[ 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3.]]])
In [111]:
np.stack([x2, 2*x2, 3*x2], axis=2)
Out[111]:
array([[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]],
[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]],
[[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.],
[ 1., 2., 3.]]])
Repetition and tiling¶
For a vector¶
In [112]:
x = np.array([1,2,3])
In [113]:
np.repeat(x, 3)
Out[113]:
array([1, 1, 1, 2, 2, 2, 3, 3, 3])
In [114]:
np.tile(x, 3)
Out[114]:
array([1, 2, 3, 1, 2, 3, 1, 2, 3])
For a matrix¶
In [115]:
x = np.arange(6).reshape((2,3))
x
Out[115]:
array([[0, 1, 2],
[3, 4, 5]])
In [116]:
np.repeat(x, 3)
Out[116]:
array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5])
In [117]:
np.repeat(x, 3, axis=0)
Out[117]:
array([[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[3, 4, 5],
[3, 4, 5],
[3, 4, 5]])
In [118]:
np.repeat(x, 3, axis=1)
Out[118]:
array([[0, 0, 0, 1, 1, 1, 2, 2, 2],
[3, 3, 3, 4, 4, 4, 5, 5, 5]])
In [119]:
np.tile(x, 3)
Out[119]:
array([[0, 1, 2, 0, 1, 2, 0, 1, 2],
[3, 4, 5, 3, 4, 5, 3, 4, 5]])
Splitting ndarrays¶
In [120]:
x = np.arange(32).reshape((4,8))
In [121]:
x
Out[121]:
array([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15],
[16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31]])
In [122]:
np.split(x, 4)
Out[122]:
[array([[0, 1, 2, 3, 4, 5, 6, 7]]),
array([[ 8, 9, 10, 11, 12, 13, 14, 15]]),
array([[16, 17, 18, 19, 20, 21, 22, 23]]),
array([[24, 25, 26, 27, 28, 29, 30, 31]])]
In [123]:
np.split(x, 4, axis=1)
Out[123]:
[array([[ 0, 1],
[ 8, 9],
[16, 17],
[24, 25]]), array([[ 2, 3],
[10, 11],
[18, 19],
[26, 27]]), array([[ 4, 5],
[12, 13],
[20, 21],
[28, 29]]), array([[ 6, 7],
[14, 15],
[22, 23],
[30, 31]])]
Vectorization¶
Example 1¶
The operators and functions (ufuncs) in Python are vectorized, and will
work element-wise over all entries in an ndarray.
In [124]:
xs = np.zeros(10, dtype='int')
for i in range(10):
xs[i] = i**2
xs
Out[124]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
In [125]:
xs = np.arange(10)**2
xs
Out[125]:
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
Using ufuncs
In [126]:
np.sqrt(xs)
Out[126]:
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
In [127]:
np.log1p(xs)
Out[127]:
array([ 0. , 0.69314718, 1.60943791, 2.30258509, 2.83321334,
3.25809654, 3.61091791, 3.91202301, 4.17438727, 4.40671925])
Example 2¶
In [128]:
n = 10
xs = np.random.rand(n)
ys = np.random.rand(n)
s = 0
for i in range(n):
s += xs[i] * ys[i]
s
Out[128]:
2.6868481407430282
In [129]:
np.dot(xs, ys)
Out[129]:
2.6868481407430282
In [130]:
xs @ ys
Out[130]:
2.6868481407430282
Example 3¶
In [131]:
m = 3
n = 2
alpha = np.random.rand(1)
betas = np.random.rand(n,1)
xs = np.random.rand(m,n)
In [132]:
alpha
Out[132]:
array([ 0.05007867])
In [133]:
betas
Out[133]:
array([[ 0.06399532],
[ 0.37993848]])
In [134]:
xs
Out[134]:
array([[ 0.79258489, 0.20951971],
[ 0.89978267, 0.044122 ],
[ 0.34222118, 0.06629664]])
Using loops¶
In [135]:
ys = np.zeros((m,1))
for i in range(m):
ys[i] = alpha
for j in range(n):
ys[i] += betas[j] * xs[i,j]
ys
Out[135]:
array([[ 0.180405 ],
[ 0.1244242 ],
[ 0.09716787]])
Removing inner loop¶
In [136]:
ys = np.zeros((m,1))
for i in range(m):
ys[i] = alpha + xs[i,:].T @ betas
ys
Out[136]:
array([[ 0.180405 ],
[ 0.1244242 ],
[ 0.09716787]])
Removing all loops¶
In [137]:
ys = alpha + xs @ betas
ys
Out[137]:
array([[ 0.180405 ],
[ 0.1244242 ],
[ 0.09716787]])
Alternative approach¶
The calculaiton with explicit intercepts and coefficients is common in deep learning, where \(\alpha\) is called the bias (\(b\)) and \(\beta\) are called the weights (\(w\)), and each equation is \(y[i] = b + w[i]*x[i]\).
It is common in statisiics to use an augmented matrix in which the first column is all ones, so that all that is needed is a single matrix multiplicaiotn.
In [138]:
X = np.c_[np.ones(m), xs]
X
Out[138]:
array([[ 1. , 0.79258489, 0.20951971],
[ 1. , 0.89978267, 0.044122 ],
[ 1. , 0.34222118, 0.06629664]])
In [139]:
alpha
Out[139]:
array([ 0.05007867])
In [140]:
betas
Out[140]:
array([[ 0.06399532],
[ 0.37993848]])
In [141]:
betas_ = np.concatenate([[alpha], betas])
betas_
Out[141]:
array([[ 0.05007867],
[ 0.06399532],
[ 0.37993848]])
In [142]:
ys = X @ betas_
ys
Out[142]:
array([[ 0.180405 ],
[ 0.1244242 ],
[ 0.09716787]])
Simulating diffusion¶
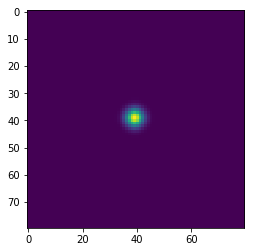
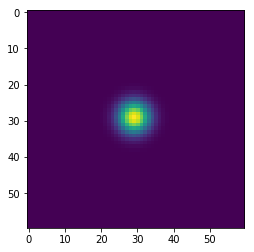
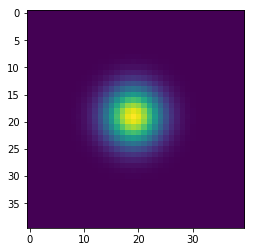
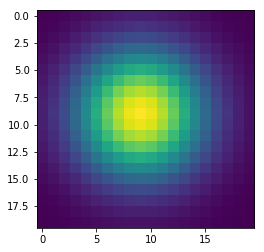
In [143]:
w = 100
h = 100
x = np.zeros((w+2,h+2), dtype='float')
x[(w//2-1):(w//2+2), (h//2-1):(h//2+2)] = 1
wts = np.ones(5)/5
for i in range(41):
if i % 10 == 0:
plt.figure()
plt.imshow(x[1:-1, 1:-1], interpolation='nearest')
center = x[1:-1, 1:-1]
left = x[:-2, 1:-1]
right = x[2:, 1:-1]
bottom = x[1:-1, :-2]
top = x[1:-1, 2:]
nbrs = np.dstack([center, left, right, bottom, top])
x = np.sum(wts * nbrs, axis=-1)