Mock Exam¶
In [1]:
%matplotlib inline
In [2]:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.linalg as la
import scipy.optimize as opt
In [3]:
%load_ext rpy2.ipython
1. (10 points)
Euclid’s algorithm for finding the greatest common divisor of two numbers is
gcd(a, 0) = a
gcd(a, b) = gcd(b, a modulo b)
- Write a function to find the greatest common divisor in Python
- What is the greatest common divisor of 17384 and 1928?
- Write a function to calculate the least common multiple
- What is the least common multiple of 17384 and 1928?
2. (10 points)
Using the iris dataset from http://goo.gl/3b3439, answer the
following questions:
- Find the mean, min and max values of all four measurements (sepal.length, sepal.width, petal.length, petal.width) for each species
- Find the average petal.width for rows where the petal.length is less than the sepal.width
3. (10 points)
Find the coordinates of the vector \(\pmatrix{1\\ 2 \\3}\) with respect to the eigenvectors of the following matrix.
array([[ 0.18673654, 0.20037016, 0.47406091],
[ 0.21715108, 0.44708353, 0.79204575],
[ 0.24299882, 0.51936745, 0.3061621 ]])
4.(20 points)
Consider the following system of equations:
- Consider the system in matrix form \(Ax=b\) and define \(A\), \(b\) in numpy.
- Show that \(A\) is positive-definite
- Use the appropriate matrix decomposition function in numpy and back-substitution to solve the system. Remember to use the structure of the problem to determine the appropriate decomposition.
5. (10 points)
The heart dataframe at https://goo.gl/CbJwQM contains information
about the survival of patients on the waiting list for the Stanford
heart transplant program.
start, stop, event: Entry and exit time and status for this interval of time
age: age-48 years
year: year of acceptance (in years after 1 Nov 1967)
surgery: prior bypass surgery 1=yes
transplant: received transplant 1=yes
id: patient id
Answer the following questions with respect to the heart data set:
- Sort the data frame by age in descending order (oldest at top) without making a copy
- How many patients received a transplant?
- What is the average age for transplanted patients under the age of 70?
- Find the mean and standard deviation of age for each value of the
transplantvariable.
6. (10 points)
You are given the following DNA sequecne in FASTA format.
dna = '''> A simulated DNA sequence.
TTAGGCAGTAACCCCGCGATAGGTAGAGCACGCAATCGTCAAGGCGTGCGGTAGGGCTTCCGTGTCTTACCCAAAGAAAC
GACGTAACGTTCCCCGGGCGGTTAAACCAAATCCACTTCACCAACGGCATAACGCGAAGCCCAAACTAAATCGCGCTCGA
GCGGACGCACATTCGCTAGGCTGTGTAGGGGCAGTCTCCGTTAAGGACGATTACCACGTGATGGTAGTTCGCAACATTGG
ACTGTCGGGAATTCCCGAAGGCACTTAAGCGGAGTCTTAGCGTACAGTAACGCAGTCCCGCGTGAACGACTGACAGATGA
'''
- Remove the comment line and combine the 4 lines of nucleotide symbols into a single string
- Count the frequency of all 16 two-letter combinations in the string.
7. (10 points)
Write a flatmap function that works like map except that the
function given takes a list and returns a list of lists that is then
flattened (4 points).
In other words, flatmap takes two arguments, a function and a list
(or other iterable), just like map. However the function given as
the first argument takes a single argument and returns a list (or other
iterable). In order to get a simple list back, we need to unravel the
resulting list of lists, hence the flatten part.
For example,
flatmap(lambda x: x.split(), ["hello world", "the quick dog"])
should return
["hello", "world", "the", "quick", "dog"]
8. (30 points)
You are given the following set of data to fit a quadratic polynomial to
x = np.arange(10)
y = np.array([ 1.58873597, 7.55101533, 10.71372171, 7.90123225,
-2.05877605, -12.40257359, -28.64568712, -46.39822281,
-68.15488905, -97.16032044])
- Find the least squares solution by using the normal equations \(A^T A \hat{x} = A^T y\). (5 points)
- Write your own gradient descent optimization function to find the
least squares solution for the coefficients \(\beta\) of a
quadratic polynomial. Do not use a gradient descent algorithm
from a package such as
scipy-optimizeorscikit-learn. You can use a simple for loop - start with the parametersbeta = np.zeros(3)with a learning rate \(\alpha = 0.0001\) and run for 100000 iterations. (15 points) - Plot the data together with the fitted polynomial. (10 points)
9. (10 points)
- Using
scipy.optimize, find the values of \(x\) and \(y\) that minimize \(e^{x^2 + y^2}\) in the unconstrained case and in the presence of the constraint that \(x + y = 3\). Use (1,1) as a starting guess.
10. (10 points)
Implement a Python function to find roots using the bisection method.
Use it to find solutions to \(x^3 + 4x^2 -3 = x\) between -4 and 1.
Do not use the standard library bisect method - the idea is to
develop the algorithm using only basic Python language constructs.
11. (10 points)
Let \(f(x)\) be a linear transformation of \(\mathbb{R}^3\) such that
Find a matrix representation for \(f\).
Compute the matrix representation for \(f\) in the basis
\[\begin{split}\begin{eqnarray*} v_1 &=& (2,3,3)\\ v_2 &=& (8,5,2)\\ v_3 &=& (1,0,5) \end{eqnarray*}\end{split}\]
12. (10 points)
A milkmaid is at point A and needs to get to point B. However, she also needs to fill a pail of water from the river en route from A to B. The equation of the river’s path is shown in the figure below. What is the minimum distance she has to travel to do this?
- Solve using
scipy.optimizeand constrained minimization. - Solve without using
scipy.optimize. Hint: Use Lagrange
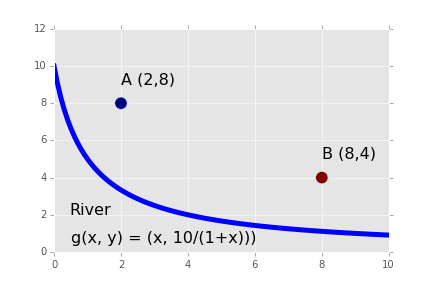
Milkmaid problem
13. (10 points)
Given the set of vectors
v1 = np.array([1,2,3])
v2 = np.array([2,4,7])
v3 = np.array([1,0,1])
- Calculate the pairwise Euclidean distance matrix
- Find an orthogonal basis for the space spanned by these vectors
without using any functions from
numpy.linagorscipy.linalg
14. (10 points)
Find the minimum of the following quadratic function on \(\mathbb{R}^4\)
and \(x\) is a column vector.
- Using scipy.optimize (4 points)
- Using a matrix decomposition method (library functions - no need to code your own). Note: for full credit you should exploit matrix structure. (4 points)
- Find the minimum under the constraint \(||x||^2 = 1\) (i.e. on the unit sphere in \(\mathbb{R}^4\)). (2 points)
**Note: Do not be overly concerned if your values for \(x\) at the minimum do not match exactly **
15. (10 points)
Given the following covariance matrix
A = np.array([[2,1],[1,4]])
- Show that the eigenvectors of \(A\) are orthogonal.
- What is the vector representing the first principal component direction?
- Find \(A^{-1}\) without performing a matrix inversion.
- What are the coordinates of the data points (0, 1) and (1, 1) in the standard basis expressed as coordinates of the principal components?
- What is the proportion of variance explained if we keep only the projection onto the first principal component?
16. (10 points)
Find the minimum of the following quadratic function on \(\mathbb{R}^2\)
Under the constraints:
- Use a matrix decomposition method to find the minimum of the
unconstrained problem without using
scipy.optimize(Use library functions - no need to code your own). Note: for full credit you should exploit matrix structure. (3 points) - Find the solution using constrained optimization with the
scipy.optimizepackage. (3 points) - Use Lagrange multipliers and solving the resulting set of equations
directly without using
scipy.optimize. (4 points)